שלום,
נראה שכבר הכרתם את אאוריקה. בטח כבר גיליתם כאן דברים מדהימים, אולי כבר שאלתם שאלות וקיבלתם תשובות טובות.
נשמח לראות משהו מכם בספר האורחים שלנו: איזו מילה טובה, חוות דעת, עצה חכמה לשיפור או כל מה שיש לכם לספר לנו על אאוריקה, כפי שאתם חווים אותה.
»
«
מהי גרפיקה ממוחשבת CGI?
הגרפיקה הממוחשבת (CGI) של ימינו היא אחד האמצעים המשוכללים ליצור אפקטים מיוחדים בסרטי קולנוע. בעוד שהאפקטים המיוחדים הפיזיים משתמשים בפירוטכניקה וחומרי נפץ, כדי ליצור אפקטים מיוחדים שמחקים פעולות ודברים שלרוב קיימים במציאות, יכולים המחשבים לאפשר דברים שאין להם מקבילות במציאות.
האפקטים הממוחשבים הם טכנולוגיה שבה ניתן בעזרת תוכנות מיוחדות לייצר דימויים קולנועיים שאינם אפשריים אחרת. הוספה של חפצים לצילום, שיפור ותיקון פגמים בצילום וכדומה - כל אלה הפכו בשנים האחרונות לנפוצים מאד בקולנוע המודרני.
צילומי חלל מדהימים, סצנות מלחמה דימיוניות, פיתוחים עתידניים מרתקים ועוד - את כל אלה ניתן כיום ליצור בקלות יחסית על גבי מסך המחשב, בעזרת תוכנות ה-CGI.
אגב, בעידן הנוכחי יש כבר תחומים ספציפיים עם ראשי תיבות כמו VFX לאפקטים ויזואליים ו-SFX לאפקטים מיוחדים.
אפקטים מיוחדים ממוחשבים שכאלה הופיעו בסרטים ידועים כמו טרילוגיית סרטי "המטריקס", הסרט "אווטאר", טרילוגיית "שר הטבעות", הסרט "טיטאניק" ועוד.
הנה מומחה האפקטים המיוחדים רוי פקר מדגים נהדר את האפשרויות:
https://youtu.be/gYu4esqvnQ0
השימוש בקולנוע שעושים בגרפיקת CGI ממוחשבת:
https://youtu.be/7rk0279i7vM
בואו ניקח פנים אנושיות ונראה הדגמה של אפשרויות גרפיקת המחשב המתוחכמת:
https://youtu.be/HjHiC0mt4Ts
אפקטים בסרטים מפורסמים שנעשו על ידי מחשב:
http://youtu.be/QyFOyMehSMg
ומה ההבדלים בין CGI, VFX ו-SFX?
https://youtu.be/Pok6EN3cfA4?long=yes
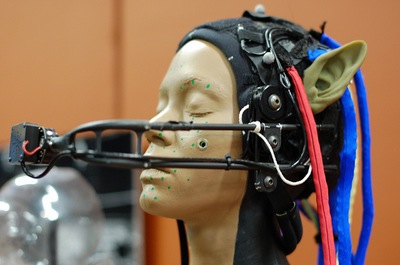איך מדמים תנועה אמיתית בדמויות אנימציה?
טכניקת "לכידת התנועה" (Motion Capture) היא שיטה שבה ניתן להקנות לדמויות אנימציה שיוצרו בעזרת מחשב, תנועה אמינה ומשכנעת שמזכירה את התנועה האנושית.
השיטה היא "להקליט" תנועות של שחקנים אנושיים בעזרת חיישנים וציוד מיוחד שקולט את התנועה ומתרגם אותה לקוד דיגיטלי. אותו הקוד משמש לאחר מכן על מנת להקנות לדמויות הממוחשבות את התנועה הריאליסטית, שמזכירה ומחקה את תנועות השחקנים בצורה מדויקת.
בעזרת שיטת לכידת תנועה הצליחו להקנות תנועה כמו-אנושית לדמויות ממוחשבות של יצורים דמויי אנוש, ביניהם היצורים הכמו-אנושיים שנקראים "נאבי" מהסרט "אוואטאר", גולום מהסרט "שר הטבעות". או מהסרט "כוכב קופים: השחר".
שחקנים כמו אנדי סרקיס הפכו למומחים כה מיומנים ללכידת תנועה, שנוהגים להקליט את תנועותיהם לצורך הקניית תנועה דמויות בדיוניות שכאלה.
כיום מיושמות טכניקות עוד יותר משוכללות, כמו "לכידת הופעה" (Performance Capture). בטכניקה זו ניתן להקליט ברזולוציה גבוהה וברמת דיוק מעולה, גם את התנועות וגם את הבעות הפנים של השחקנים ולהצמידן לדמויות האנימציה.
זה מול זה - כך הופכת לכידת תנועה ושיחה לאנימציה משוכללת:
https://youtu.be/O4jXbMMdn-I
טכניקת לכידת התנועה בצילום של מוות לסרטים:
https://youtu.be/SO08s3ALiyQ
כך מצלמים כלב עטוף חיישנים לסרט:
https://youtu.be/9rr2TJj8U0E
וקדימון הסרט "כוכב קופים: השחר", שחלק גדול מהתנועות של הקופים שבו הוקלטו בעזרת לכידת תנועה:
http://youtu.be/Km0QV9vGjnA
איך מעבירים הבעות פנים מבני אדם לדמויות אנימציה?
בעשורים האחרונים מגיעה האנימציה בסרטים לרמות מדהימות של רגש בקרב הדמויות המצוירות בהם. אם פעם היו פניהם של מיקי מאוס ודונלד דאק חתומות כמעט לחלוטין, היום הבעות הפנים של דמויות אנימציה מביעות רגש, מכעס ורוגז ועד חמלה ואהבה.
מה שמאפשר את הקידמה המדהימה הזו בתעשיית האנימציה הוא המשתנה ששינה את העולם בחצי מאה האחרונה כמעט בכל תחום אפשרי. מדובר כמובן במחשב.
טכניקת "לכידת הופעה" (Performance Capture) היא שיטה מבוססת טכנולוגיה שבה ניתן להעביר לדמויות אנימציה שיוצרו בעזרת מחשב.
בטכניקה זו ניתן להקליט אל המחשב, ברזולוציה גבוהה וברמת דיוק מעולה, גם את התנועות וגם את הבעות הפנים של השחקנים. לאחר מכן מצמידים במחשב את ההבעות ואת התנועה של שרירי הפנים אל דמויות האנימציה שבסרט ומקבלים מחוות מדויקות ומרשימות במיוחד מהדמויות המצוירות.
הנה יוצר סרטי אווטאר ג'יימס קאמרון מסביר שבלכידת הופעה צריך להיזהר מ"עמק המוזרות" של הדמיון המקריפ לבני אדם:
https://youtu.be/1wK1Ixr-UmM
"לכידת ההופעה" המדהימה שנעשתה בסרט "כוכב קופים: השחר":
https://youtu.be/4NU9ikjqjC0
הדגמה בחברת אימייג'מטריקס, מהמתקדמות בטכנולוגיה הזו:
https://youtu.be/JF_NFmtw89g
והטכניקה המדהימה הזו היא חלק מ"לכידת התנועה" בהוליווד:
https://youtu.be/2CJ26DEu3E0
מהי הגאומטריה הפרקטלית של מנדלברוט?
בנואה מנדלברוט היה מתמטיקאי שמצא שיש צורות רבות שכל חלק שלהן הוא כמו השלם, או מזכיר אותו. מדידה של שטח הפנים של צורות כאלה תלוייה ביכולת שלנו לבחון אותו, מכיוון שככל שנתקרב אל העצם, נגלה חספוס הולך וגובר, שיגדיל את שטח הפנים.
מנדלברוט מצא שכלל מתמטי פשוט, או נוסחה פשוטה, יכולים להגדיר מצוין את העצם שנראה שאין בו חוקיות או היגיון כלשהם.
אגב, בנואה מנדלברוט עצמו מעדיף את המונח "חספוס" ולא אי-יציבות או אי-סדר, מכיוון שהוא רואה סדר בכל דבר ואין בעיניו שום דבר שאין בו סדר מסוים. להוכחה, המילה "פרקטל" שהוא בחר לתיאור של המחוספס והשבור באה מהמילה הלטינית פרקטוס (fractus), שפירושה "שבור".
למשל בכרובית הוא רואה גם תחכום וגם פשטות. אותם קונוסים שאנו רואים בברוקולי, חוזרים גם אם נביט בחלק מקונוס כזה ויחזרו שוב ושוב בכל קנה מידה שנביט בו. כך יהיה גם בעננים, בקווי חוף עם מפרצים בגדלים (מפיורדים עצומים ועד מפרצונים בגוגל מילימטרים), עצים (בהם עורקי העלה נראים כענפים וענפי העץ דומים לעצים) ועוד המון צורות שהן לכאורה אקראיות ולא בנויות בסדר של ממש, אבל כשנביט בחלק מהם נראה בגדלים שונים, תבנית דומה לזו שראינו בעצם המלא.
איך זה מסתדר? - ובכן, בכולם יש מרכיב שניתן למצוא והוא "הדמיון העצמי" (Self similarity), שבו אותה צורה חוזרת שוב ושוב, ככל שנתקרב. ומסתבר שאותה צורה שבה ענפים יוצאים מענפים בעץ, היא גם הצורה של צינורות הדם בגופנו, נימי העלים של העץ, נהרות על פני כדור הארץ וכן הלאה. מסתבר שהטבע עושה שימוש בחוק זהה להמון מקרים שאינם קשורים זה בזה ושכביכול אין בהם שום סדר הגיוני.
ל"דמיון העצמי" מנדלברוט קרא "פרקטל". הוא גם הבין שניתן לעבוד עם הפרקטלים הפוך ולהשתמש בסדרה של חוקים מתמטיים פשוטים, כדי לייצר צורות כאלה. בסוף שנות ה-50 הוא השתמש במחשב כדי לייצר צורות כאלה. הוא עשה מהפכה של ממש בגאומטריה, שכן הוא החל לקרב אותה לעולם הטבע.
אם קודם לפרקטלים לא סייעה הגאומטריה לתאר את הצורות של גורמים בטבע, כמו הרים, עננים, עצים, ירקות וקווי חוף, הרי שהפרקטל, שמסייע למצוא סדר בדפוסים מורכבים ביותר, שינה את זה והראה את הסדר המתמטי שבו מתנהל הטבע והעולם הכאוטי. או במילים שלו כפי שכתב בהקדמת ספרו "עננים הם לא כדורים, הרים אינם בעלי צורה של חרוט, קו החוף לא עשוי ממעגלים, קליפת העץ איננה חלקה והברק אינו מתקדם בקו ישר".
בחייו סבל מנדלברוט לא מעט בשל הפרקטלים. הממסד המתמטי ממש נידה אותו בשל ההתעסקות בתמונות, שלא יאה למתמטיקאי רציני. מי שהצילה אותו מחוסר תעסוקה הייתה חברת IBM, שלא זו בלבד שהעסיקה אותו במרכז המחקר שלה, אלא אף נתנה לו לעשות כרצונו. בעזרת חוק רקורסיבי פשוט מאוד הוא מצליח עתה לייצר תמונות בעלות מורכבות הולכת וגדלה, בה רואים ברמות שונות, כאמור, צורות דומות.
גם הציבור הרחב מתחיל להתחבר לרעיונות שלו, שבניגוד לרעיונות מתמטיים רגילים, קל להבינם. מה עוד שניתן היה לראותם לפתע, בתוצרי מחשב מודפסים. את הצד הגרפי של הפרקטלים ניתן היה גם לחקור וליישם באדריכלות, בעיצוב מוצר ובתעשיות שונות.
וכך זוכה מי שכילד בן 12 הפך לפליט פולני בצרפת ולימד את עצמו מתמטיקה לבדו, הוא זוכה בשלב מסוים בציבור לכינוי "כוכב הרוק של המתמטיקה". כי גם אם רעיונותיו על הפרקטלים עדיין לא מתקבלים אצל הקהילה המדעית, מעל ראשם הוא הופך די מהר לאחד המתמטיקאים המשפיעים בהיסטוריה.
הנה סרטון שמסביר את התגלית של מנדלברוט:
http://youtu.be/Dm-zy5f4qIo
אלה לא הפרקטלים היחידים בטבע:
https://youtu.be/w_MNQBWQ5DI
וראו כמה נם יפים ומרהיבים:
https://youtu.be/YkApFcYsP30
הדמיון העצמי של פרקטל:
http://youtu.be/9G6uO7ZHtK8
הסבריו של מנדלברוט עצמו:
http://youtu.be/pDajf3PXpNI
דוגמאות שונות לסט מנדלברוט, שמערב סיבוכיות, הרמוניה ויופי בשימוש בנוסחאות פשוטות:
http://youtu.be/G_GBwuYuOOs
והרצאת טד של מנדלברוט עצמו (מתורגם):
https://youtu.be/ay8OMOsf6AQ?long=yes
מהם פרקטלים?
הפרקטל הוא צורה שככל שנביט בה קרוב יותר, נראה את אותה הצורה חוזרת על עצמה בכל קנה מידה. זוהי צורה גאומטרית שמורכבת פנימה, שוב ושוב, מעותקים של עצמה, מוקטנים יותר ויותר. ככל שנתבונן לתוך חלקי הפרקטל, נראה שם תמיד חלקים הדומים לו, כך שכל פרט זעיר בצורה, דומה לצורה המקורית והגדולה ביותר.
בגרפיקה ממוחשבת עושים המון שימוש בפרקטלים. הסיבה היא שנוסחאות מתמטיות קלות יחסית מאפשרות ליצור הרים ומרקמים מורכבים ליצירה בצורה אחרת. גם בפיזיקה משתמשים בפרקטלים למחקרים על תורת הכאוס וכדומה.
בטבע אפשר לראות מבנים שונים שדומים לפרקטלים. מבנים בטבע כמו צורת הכרובית, מבנה העורקים של העלה, התפצלות כלי הדם בגוף, פתית שלג או צורת קו חוף (במיוחד של הפיורדים בנורווגיה) - כל אלה מזכירים מאד את הפרקטלים ומראים שבטבע יש שיטה גם בדברים שאינם מובנים בצורה מתמטית.
הנה סרטון הסבר למושג הפרקטל (מתורגם):
http://youtu.be/Tm0U2VxFd8Q
הסבר מילולי על הפרקטלים - מהתבניות היותר מעניינות שבטבע (עברית):
http://youtu.be/ofA2tBvcbhw?t=3m38s
המתמטיקה של הפרקטלים בסרטון מקסים לפי ז'אנר הסרט האפל (מתורגם):
https://youtu.be/0C75vRVL5lE
הפרקטלים שבטבע:
https://youtu.be/XwWyTts06tU
עוד פרקטלים בטבע:
https://youtu.be/dZM45mfJQ40
להדגמת הרקורסיה הפשוטה, הנה משולש סרפינסקי שלא נגמר:
http://youtu.be/QsMvoui5WlQ?t=10s
ופרקטל מתמטי ללא סוף, בגרפיקה ממוחשבת ואנימציה מוסיקה נהדרים:
https://youtu.be/hRrBnI5L0u8?long=yes
איפה יש פרקטלים בטבע?
ודאי היכרתם או קראתם באאוריקה על הפרקטלים, אותן צורות מתמטיות מיוחדות שהתגלו על ידי חוקר הפרקטלים בנואה מנדלברוט והעסיקו חוקרים רבים מתחילת המאה ה-20.
את הפרקטלים ניתן לזהות בכך שיש להם דמיון עצמי. כלומר, כל חלק בהם דומה לדבר השלם. גם בטבע ישנם לא מעט דברים שאם נביט בחלק קטן מהם נגלה את אותה צורה של השלם - בקנה מידה קטן. וגם בחלק הקטן הזה, אם נביט בעזרת זכוכית מגדלת, נוכל לראות שחלקיו שלו דומים גם הם לשלם וחלק הזה וכך זה יכול להמשיך עוד ועוד פנימה. תמיד אותה צורה ושמה...
אז אומרים לכם שכל כך הרבה פרקטלים יש בטבע ואפשר לראותם כמעט בכל מקום. אבל איפה זה בדיוק בכל מקום?
ובכן, בכרובית, בברקים, בריאות, שרכים, מפלים, בפתיתי שלג, בנימי העלה, בענפי העצים, גבישי הקרח, בענני קומולוס, בכלי הדם שלנו, בבועות סבון, בחופי ים מפורצים של פיורדים נורווגיים או בחופי אגמים כמו אגם נאצר שבמצרים, בשוניות אלמוגים במעמקי הים ועד לגלקסיות הענקיות שבחלל.
כן. בטבע נוכל למצוא צורות רבות שיש להן תכונות פרקטליות. דוגמה מפורטת היא לצלם את אורכו של חוף ים ממטוס ולראות שצורתו דומה מאד לזו שנראה בטיול לאורך החוף, כשנביט בפרטים הקטנים שלו. גם מדידת אורכו של קו החוף תגלה לנו דבר מדהים - אורכו הוא בפשטות אינסופי. זה קורה משום שקנה המידה משפיע על המדידה. אם נחשב אורך חוף מתמונת לוויין נקבל אורך קטן בהרבה מזה שיתקבל אם נמדוד את הדרך שעושה נמלה ההולכת לאורכו. הסיבה היא שהשיפולים והשיפועים שחווה הנמלה בקו החוף מאריכים לה את הדרך בטירוף. זה סוג של פרקטל - הנמלה רואה את צורת קו החוף, שהיא זהה לצורה שמצלם הלווים מהחלל.
פרקטלית היא גם הכרובית למשל. אם נחתוך אותה לאורך, נראה שיש בה התפצלויות שיוצרות המון כרוביות קטנות, שבעצמן מתפצלות כל אחת לכרוביות זעירות, שבכל אחת יש כרוביות מיקרוסקופיות והלאה.
בצורה דומה מתפצלות הריאות שלנו או כלי הדם שבגופנו. אבל אתם לא יכולים להביט אל תוך הלב, אז קחו עלה של עץ או שיח ושימו לב לנימים של העלה. נכון שהם מסתעפים ומתפצלים עוד ועוד, כשמכל נים יוצאים נימים קטנים, שמהם יוצאים נימים זעירים וכך הלאה? - גם בכלי הדם שבגופנו יוצאים כך עשרות כלי דם קטנים מכל אחד, בתבנית החוזרת על עצמה שוב ושוב, עד לנימים זעירים ודקיקים במיוחד.
הנה הפרקטלים שבטבע ותגליתו של מנדלברוט:
https://youtu.be/w_MNQBWQ5DI
הסבר הפרקטלים שבטבע:
https://youtu.be/Tm0U2VxFd8Q
שלל פרקטלים טבעיים:
https://youtu.be/4IRLvYOZD8A
עוד פרקטלים בטבע:
https://youtu.be/XwWyTts06tU
ואובייקטים טבעיים שהם פרקטלים:
https://youtu.be/dZM45mfJQ40
מהי קליגרפיה והכתיבה הקישוטית שבה?
קליגרפיה (Calligraphy), או כתיבה תמה, היא אמנות הכתיבה ובדרך כלל היא מתייחסת לכתיבה מסוגננת. זוהי אמנות הכתיבה הקישוטית.
מקורה של אמנות הקליגרפיה הוא באמנות קדומה של סין ומזרח אסיה במאה ה-4 לספירה. משם היא התפתחה והתפשטה לפרס ולארצות האיסלאם, שבה תופס הכתב המסוגנן מקום מקודש והתפתחה מסורת קליגרפית עשירה. גם ביהדות התייחסו לסופרי הסת"ם, מי שכתבו את ספרי התורה, בכבוד רב. בצד מעמדם הדתי, הם נחשבו גם בעלי סגנון אישי ואמנותי.
גם בעולם המערבי התפתחה הקליגרפיה, בתוך המעבר מאותיות יווניות לאותיות לטיניות וכתיבה של כתבי-דת לטיניים מעוטרים ומאוירים. בימי הביניים פותחו סגנונות כתיבה, כמו האותיות האוּנקִייליוֹת שהיו נהוגות באי האנגלי, המינוסקול הקרולינגי והכתב הגותי שפותחו בגרמניה והכתב הנטוי שפותח באיטליה.
במאה ה-19, לאחר שמאז המצאת הדפוס ירדה קרנה של הקליגרפיה, חזרו אמני קליגרפיה לפעול. במאה ה-20 חזרה הקליגרפיה לפרוח בציורי גרפיטי ובעולם המחשבים. זה קרה בעיקר מאז המצאת המחשב האישי ומעבדי התמלילים, על מגוון הגופנים (פונטים) שפותחו בשבילם.
דמות מרכזית בקידום הנושא היה סטיב ג'ובס, מנכ"ל אפל האגדי, שבצעירותו קיבל קורס קליגרפיה באוניברסיטה והושפע מהיופי של עולם האותיות והעיצוב. כשפיתח ג'ובס את מחשב המקינטוש, הוא הפך אותו למחשב גרפי שגופנים מעוצבים ומעוררי השראה ויופי תפסו בו מקום מרכזי.
קליגרפיה נקראת לעיתים בעברית "כתיבה תמה". מקור המילה בשפה היוונית: המלה "קאלוס" פירושה ביוונית "יופי" ו"גראפוס" היא ביוונית "כתיבה".
הנה הקליגרפיה הסינית הקדומה:
https://youtu.be/ppZWIwZsRdU
על קליגרף סיני שעשה לו שם בעולם (עברית):
https://youtu.be/d68TIY2_4H4
אוסף קליגרפיות מרהיבות:
https://youtu.be/zg7QLW0KrQw
מדריך מהיר לקליגרפיה מעשית:
https://youtu.be/Rnlha-GLL5s
קליגרפיה במחשב המקינטוש - הראשון שהעמיד במרכז את העיצוב הגרפי והקליגרפיה:
http://youtu.be/2B-XwPjn9YY?t=1m15s
יופייה של הקליגרפיה ביפאן (עברית):
http://youtu.be/cUI9PPeUCmI
והדגמה של הקליגרפיה היפנית (עברית):
http://youtu.be/geQtLi66W-A
הגרפיקה הממוחשבת (CGI) של ימינו היא אחד האמצעים המשוכללים ליצור אפקטים מיוחדים בסרטי קולנוע. בעוד שהאפקטים המיוחדים הפיזיים משתמשים בפירוטכניקה וחומרי נפץ, כדי ליצור אפקטים מיוחדים שמחקים פעולות ודברים שלרוב קיימים במציאות, יכולים המחשבים לאפשר דברים שאין להם מקבילות במציאות.
האפקטים הממוחשבים הם טכנולוגיה שבה ניתן בעזרת תוכנות מיוחדות לייצר דימויים קולנועיים שאינם אפשריים אחרת. הוספה של חפצים לצילום, שיפור ותיקון פגמים בצילום וכדומה - כל אלה הפכו בשנים האחרונות לנפוצים מאד בקולנוע המודרני.
צילומי חלל מדהימים, סצנות מלחמה דימיוניות, פיתוחים עתידניים מרתקים ועוד - את כל אלה ניתן כיום ליצור בקלות יחסית על גבי מסך המחשב, בעזרת תוכנות ה-CGI.
אגב, בעידן הנוכחי יש כבר תחומים ספציפיים עם ראשי תיבות כמו VFX לאפקטים ויזואליים ו-SFX לאפקטים מיוחדים.
אפקטים מיוחדים ממוחשבים שכאלה הופיעו בסרטים ידועים כמו טרילוגיית סרטי "המטריקס", הסרט "אווטאר", טרילוגיית "שר הטבעות", הסרט "טיטאניק" ועוד.
הנה מומחה האפקטים המיוחדים רוי פקר מדגים נהדר את האפשרויות:
https://youtu.be/gYu4esqvnQ0
השימוש בקולנוע שעושים בגרפיקת CGI ממוחשבת:
https://youtu.be/7rk0279i7vM
בואו ניקח פנים אנושיות ונראה הדגמה של אפשרויות גרפיקת המחשב המתוחכמת:
https://youtu.be/HjHiC0mt4Ts
אפקטים בסרטים מפורסמים שנעשו על ידי מחשב:
http://youtu.be/QyFOyMehSMg
ומה ההבדלים בין CGI, VFX ו-SFX?
https://youtu.be/Pok6EN3cfA4?long=yes
טכניקת "לכידת התנועה" (Motion Capture) היא שיטה שבה ניתן להקנות לדמויות אנימציה שיוצרו בעזרת מחשב, תנועה אמינה ומשכנעת שמזכירה את התנועה האנושית.
השיטה היא "להקליט" תנועות של שחקנים אנושיים בעזרת חיישנים וציוד מיוחד שקולט את התנועה ומתרגם אותה לקוד דיגיטלי. אותו הקוד משמש לאחר מכן על מנת להקנות לדמויות הממוחשבות את התנועה הריאליסטית, שמזכירה ומחקה את תנועות השחקנים בצורה מדויקת.
בעזרת שיטת לכידת תנועה הצליחו להקנות תנועה כמו-אנושית לדמויות ממוחשבות של יצורים דמויי אנוש, ביניהם היצורים הכמו-אנושיים שנקראים "נאבי" מהסרט "אוואטאר", גולום מהסרט "שר הטבעות". או מהסרט "כוכב קופים: השחר".
שחקנים כמו אנדי סרקיס הפכו למומחים כה מיומנים ללכידת תנועה, שנוהגים להקליט את תנועותיהם לצורך הקניית תנועה דמויות בדיוניות שכאלה.
כיום מיושמות טכניקות עוד יותר משוכללות, כמו "לכידת הופעה" (Performance Capture). בטכניקה זו ניתן להקליט ברזולוציה גבוהה וברמת דיוק מעולה, גם את התנועות וגם את הבעות הפנים של השחקנים ולהצמידן לדמויות האנימציה.
זה מול זה - כך הופכת לכידת תנועה ושיחה לאנימציה משוכללת:
https://youtu.be/O4jXbMMdn-I
טכניקת לכידת התנועה בצילום של מוות לסרטים:
https://youtu.be/SO08s3ALiyQ
כך מצלמים כלב עטוף חיישנים לסרט:
https://youtu.be/9rr2TJj8U0E
וקדימון הסרט "כוכב קופים: השחר", שחלק גדול מהתנועות של הקופים שבו הוקלטו בעזרת לכידת תנועה:
http://youtu.be/Km0QV9vGjnA
בעשורים האחרונים מגיעה האנימציה בסרטים לרמות מדהימות של רגש בקרב הדמויות המצוירות בהם. אם פעם היו פניהם של מיקי מאוס ודונלד דאק חתומות כמעט לחלוטין, היום הבעות הפנים של דמויות אנימציה מביעות רגש, מכעס ורוגז ועד חמלה ואהבה.
מה שמאפשר את הקידמה המדהימה הזו בתעשיית האנימציה הוא המשתנה ששינה את העולם בחצי מאה האחרונה כמעט בכל תחום אפשרי. מדובר כמובן במחשב.
טכניקת "לכידת הופעה" (Performance Capture) היא שיטה מבוססת טכנולוגיה שבה ניתן להעביר לדמויות אנימציה שיוצרו בעזרת מחשב.
בטכניקה זו ניתן להקליט אל המחשב, ברזולוציה גבוהה וברמת דיוק מעולה, גם את התנועות וגם את הבעות הפנים של השחקנים. לאחר מכן מצמידים במחשב את ההבעות ואת התנועה של שרירי הפנים אל דמויות האנימציה שבסרט ומקבלים מחוות מדויקות ומרשימות במיוחד מהדמויות המצוירות.
הנה יוצר סרטי אווטאר ג'יימס קאמרון מסביר שבלכידת הופעה צריך להיזהר מ"עמק המוזרות" של הדמיון המקריפ לבני אדם:
https://youtu.be/1wK1Ixr-UmM
"לכידת ההופעה" המדהימה שנעשתה בסרט "כוכב קופים: השחר":
https://youtu.be/4NU9ikjqjC0
הדגמה בחברת אימייג'מטריקס, מהמתקדמות בטכנולוגיה הזו:
https://youtu.be/JF_NFmtw89g
והטכניקה המדהימה הזו היא חלק מ"לכידת התנועה" בהוליווד:
https://youtu.be/2CJ26DEu3E0
בנואה מנדלברוט היה מתמטיקאי שמצא שיש צורות רבות שכל חלק שלהן הוא כמו השלם, או מזכיר אותו. מדידה של שטח הפנים של צורות כאלה תלוייה ביכולת שלנו לבחון אותו, מכיוון שככל שנתקרב אל העצם, נגלה חספוס הולך וגובר, שיגדיל את שטח הפנים.
מנדלברוט מצא שכלל מתמטי פשוט, או נוסחה פשוטה, יכולים להגדיר מצוין את העצם שנראה שאין בו חוקיות או היגיון כלשהם.
אגב, בנואה מנדלברוט עצמו מעדיף את המונח "חספוס" ולא אי-יציבות או אי-סדר, מכיוון שהוא רואה סדר בכל דבר ואין בעיניו שום דבר שאין בו סדר מסוים. להוכחה, המילה "פרקטל" שהוא בחר לתיאור של המחוספס והשבור באה מהמילה הלטינית פרקטוס (fractus), שפירושה "שבור".
למשל בכרובית הוא רואה גם תחכום וגם פשטות. אותם קונוסים שאנו רואים בברוקולי, חוזרים גם אם נביט בחלק מקונוס כזה ויחזרו שוב ושוב בכל קנה מידה שנביט בו. כך יהיה גם בעננים, בקווי חוף עם מפרצים בגדלים (מפיורדים עצומים ועד מפרצונים בגוגל מילימטרים), עצים (בהם עורקי העלה נראים כענפים וענפי העץ דומים לעצים) ועוד המון צורות שהן לכאורה אקראיות ולא בנויות בסדר של ממש, אבל כשנביט בחלק מהם נראה בגדלים שונים, תבנית דומה לזו שראינו בעצם המלא.
איך זה מסתדר? - ובכן, בכולם יש מרכיב שניתן למצוא והוא "הדמיון העצמי" (Self similarity), שבו אותה צורה חוזרת שוב ושוב, ככל שנתקרב. ומסתבר שאותה צורה שבה ענפים יוצאים מענפים בעץ, היא גם הצורה של צינורות הדם בגופנו, נימי העלים של העץ, נהרות על פני כדור הארץ וכן הלאה. מסתבר שהטבע עושה שימוש בחוק זהה להמון מקרים שאינם קשורים זה בזה ושכביכול אין בהם שום סדר הגיוני.
ל"דמיון העצמי" מנדלברוט קרא "פרקטל". הוא גם הבין שניתן לעבוד עם הפרקטלים הפוך ולהשתמש בסדרה של חוקים מתמטיים פשוטים, כדי לייצר צורות כאלה. בסוף שנות ה-50 הוא השתמש במחשב כדי לייצר צורות כאלה. הוא עשה מהפכה של ממש בגאומטריה, שכן הוא החל לקרב אותה לעולם הטבע.
אם קודם לפרקטלים לא סייעה הגאומטריה לתאר את הצורות של גורמים בטבע, כמו הרים, עננים, עצים, ירקות וקווי חוף, הרי שהפרקטל, שמסייע למצוא סדר בדפוסים מורכבים ביותר, שינה את זה והראה את הסדר המתמטי שבו מתנהל הטבע והעולם הכאוטי. או במילים שלו כפי שכתב בהקדמת ספרו "עננים הם לא כדורים, הרים אינם בעלי צורה של חרוט, קו החוף לא עשוי ממעגלים, קליפת העץ איננה חלקה והברק אינו מתקדם בקו ישר".
בחייו סבל מנדלברוט לא מעט בשל הפרקטלים. הממסד המתמטי ממש נידה אותו בשל ההתעסקות בתמונות, שלא יאה למתמטיקאי רציני. מי שהצילה אותו מחוסר תעסוקה הייתה חברת IBM, שלא זו בלבד שהעסיקה אותו במרכז המחקר שלה, אלא אף נתנה לו לעשות כרצונו. בעזרת חוק רקורסיבי פשוט מאוד הוא מצליח עתה לייצר תמונות בעלות מורכבות הולכת וגדלה, בה רואים ברמות שונות, כאמור, צורות דומות.
גם הציבור הרחב מתחיל להתחבר לרעיונות שלו, שבניגוד לרעיונות מתמטיים רגילים, קל להבינם. מה עוד שניתן היה לראותם לפתע, בתוצרי מחשב מודפסים. את הצד הגרפי של הפרקטלים ניתן היה גם לחקור וליישם באדריכלות, בעיצוב מוצר ובתעשיות שונות.
וכך זוכה מי שכילד בן 12 הפך לפליט פולני בצרפת ולימד את עצמו מתמטיקה לבדו, הוא זוכה בשלב מסוים בציבור לכינוי "כוכב הרוק של המתמטיקה". כי גם אם רעיונותיו על הפרקטלים עדיין לא מתקבלים אצל הקהילה המדעית, מעל ראשם הוא הופך די מהר לאחד המתמטיקאים המשפיעים בהיסטוריה.
הנה סרטון שמסביר את התגלית של מנדלברוט:
http://youtu.be/Dm-zy5f4qIo
אלה לא הפרקטלים היחידים בטבע:
https://youtu.be/w_MNQBWQ5DI
וראו כמה נם יפים ומרהיבים:
https://youtu.be/YkApFcYsP30
הדמיון העצמי של פרקטל:
http://youtu.be/9G6uO7ZHtK8
הסבריו של מנדלברוט עצמו:
http://youtu.be/pDajf3PXpNI
דוגמאות שונות לסט מנדלברוט, שמערב סיבוכיות, הרמוניה ויופי בשימוש בנוסחאות פשוטות:
http://youtu.be/G_GBwuYuOOs
והרצאת טד של מנדלברוט עצמו (מתורגם):
https://youtu.be/ay8OMOsf6AQ?long=yes
גרפיקה ממוחשבת
הפרקטל הוא צורה שככל שנביט בה קרוב יותר, נראה את אותה הצורה חוזרת על עצמה בכל קנה מידה. זוהי צורה גאומטרית שמורכבת פנימה, שוב ושוב, מעותקים של עצמה, מוקטנים יותר ויותר. ככל שנתבונן לתוך חלקי הפרקטל, נראה שם תמיד חלקים הדומים לו, כך שכל פרט זעיר בצורה, דומה לצורה המקורית והגדולה ביותר.
בגרפיקה ממוחשבת עושים המון שימוש בפרקטלים. הסיבה היא שנוסחאות מתמטיות קלות יחסית מאפשרות ליצור הרים ומרקמים מורכבים ליצירה בצורה אחרת. גם בפיזיקה משתמשים בפרקטלים למחקרים על תורת הכאוס וכדומה.
בטבע אפשר לראות מבנים שונים שדומים לפרקטלים. מבנים בטבע כמו צורת הכרובית, מבנה העורקים של העלה, התפצלות כלי הדם בגוף, פתית שלג או צורת קו חוף (במיוחד של הפיורדים בנורווגיה) - כל אלה מזכירים מאד את הפרקטלים ומראים שבטבע יש שיטה גם בדברים שאינם מובנים בצורה מתמטית.
הנה סרטון הסבר למושג הפרקטל (מתורגם):
http://youtu.be/Tm0U2VxFd8Q
הסבר מילולי על הפרקטלים - מהתבניות היותר מעניינות שבטבע (עברית):
http://youtu.be/ofA2tBvcbhw?t=3m38s
המתמטיקה של הפרקטלים בסרטון מקסים לפי ז'אנר הסרט האפל (מתורגם):
https://youtu.be/0C75vRVL5lE
הפרקטלים שבטבע:
https://youtu.be/XwWyTts06tU
עוד פרקטלים בטבע:
https://youtu.be/dZM45mfJQ40
להדגמת הרקורסיה הפשוטה, הנה משולש סרפינסקי שלא נגמר:
http://youtu.be/QsMvoui5WlQ?t=10s
ופרקטל מתמטי ללא סוף, בגרפיקה ממוחשבת ואנימציה מוסיקה נהדרים:
https://youtu.be/hRrBnI5L0u8?long=yes
ודאי היכרתם או קראתם באאוריקה על הפרקטלים, אותן צורות מתמטיות מיוחדות שהתגלו על ידי חוקר הפרקטלים בנואה מנדלברוט והעסיקו חוקרים רבים מתחילת המאה ה-20.
את הפרקטלים ניתן לזהות בכך שיש להם דמיון עצמי. כלומר, כל חלק בהם דומה לדבר השלם. גם בטבע ישנם לא מעט דברים שאם נביט בחלק קטן מהם נגלה את אותה צורה של השלם - בקנה מידה קטן. וגם בחלק הקטן הזה, אם נביט בעזרת זכוכית מגדלת, נוכל לראות שחלקיו שלו דומים גם הם לשלם וחלק הזה וכך זה יכול להמשיך עוד ועוד פנימה. תמיד אותה צורה ושמה...
אז אומרים לכם שכל כך הרבה פרקטלים יש בטבע ואפשר לראותם כמעט בכל מקום. אבל איפה זה בדיוק בכל מקום?
ובכן, בכרובית, בברקים, בריאות, שרכים, מפלים, בפתיתי שלג, בנימי העלה, בענפי העצים, גבישי הקרח, בענני קומולוס, בכלי הדם שלנו, בבועות סבון, בחופי ים מפורצים של פיורדים נורווגיים או בחופי אגמים כמו אגם נאצר שבמצרים, בשוניות אלמוגים במעמקי הים ועד לגלקסיות הענקיות שבחלל.
כן. בטבע נוכל למצוא צורות רבות שיש להן תכונות פרקטליות. דוגמה מפורטת היא לצלם את אורכו של חוף ים ממטוס ולראות שצורתו דומה מאד לזו שנראה בטיול לאורך החוף, כשנביט בפרטים הקטנים שלו. גם מדידת אורכו של קו החוף תגלה לנו דבר מדהים - אורכו הוא בפשטות אינסופי. זה קורה משום שקנה המידה משפיע על המדידה. אם נחשב אורך חוף מתמונת לוויין נקבל אורך קטן בהרבה מזה שיתקבל אם נמדוד את הדרך שעושה נמלה ההולכת לאורכו. הסיבה היא שהשיפולים והשיפועים שחווה הנמלה בקו החוף מאריכים לה את הדרך בטירוף. זה סוג של פרקטל - הנמלה רואה את צורת קו החוף, שהיא זהה לצורה שמצלם הלווים מהחלל.
פרקטלית היא גם הכרובית למשל. אם נחתוך אותה לאורך, נראה שיש בה התפצלויות שיוצרות המון כרוביות קטנות, שבעצמן מתפצלות כל אחת לכרוביות זעירות, שבכל אחת יש כרוביות מיקרוסקופיות והלאה.
בצורה דומה מתפצלות הריאות שלנו או כלי הדם שבגופנו. אבל אתם לא יכולים להביט אל תוך הלב, אז קחו עלה של עץ או שיח ושימו לב לנימים של העלה. נכון שהם מסתעפים ומתפצלים עוד ועוד, כשמכל נים יוצאים נימים קטנים, שמהם יוצאים נימים זעירים וכך הלאה? - גם בכלי הדם שבגופנו יוצאים כך עשרות כלי דם קטנים מכל אחד, בתבנית החוזרת על עצמה שוב ושוב, עד לנימים זעירים ודקיקים במיוחד.
הנה הפרקטלים שבטבע ותגליתו של מנדלברוט:
https://youtu.be/w_MNQBWQ5DI
הסבר הפרקטלים שבטבע:
https://youtu.be/Tm0U2VxFd8Q
שלל פרקטלים טבעיים:
https://youtu.be/4IRLvYOZD8A
עוד פרקטלים בטבע:
https://youtu.be/XwWyTts06tU
ואובייקטים טבעיים שהם פרקטלים:
https://youtu.be/dZM45mfJQ40
קליגרפיה (Calligraphy), או כתיבה תמה, היא אמנות הכתיבה ובדרך כלל היא מתייחסת לכתיבה מסוגננת. זוהי אמנות הכתיבה הקישוטית.
מקורה של אמנות הקליגרפיה הוא באמנות קדומה של סין ומזרח אסיה במאה ה-4 לספירה. משם היא התפתחה והתפשטה לפרס ולארצות האיסלאם, שבה תופס הכתב המסוגנן מקום מקודש והתפתחה מסורת קליגרפית עשירה. גם ביהדות התייחסו לסופרי הסת"ם, מי שכתבו את ספרי התורה, בכבוד רב. בצד מעמדם הדתי, הם נחשבו גם בעלי סגנון אישי ואמנותי.
גם בעולם המערבי התפתחה הקליגרפיה, בתוך המעבר מאותיות יווניות לאותיות לטיניות וכתיבה של כתבי-דת לטיניים מעוטרים ומאוירים. בימי הביניים פותחו סגנונות כתיבה, כמו האותיות האוּנקִייליוֹת שהיו נהוגות באי האנגלי, המינוסקול הקרולינגי והכתב הגותי שפותחו בגרמניה והכתב הנטוי שפותח באיטליה.
במאה ה-19, לאחר שמאז המצאת הדפוס ירדה קרנה של הקליגרפיה, חזרו אמני קליגרפיה לפעול. במאה ה-20 חזרה הקליגרפיה לפרוח בציורי גרפיטי ובעולם המחשבים. זה קרה בעיקר מאז המצאת המחשב האישי ומעבדי התמלילים, על מגוון הגופנים (פונטים) שפותחו בשבילם.
דמות מרכזית בקידום הנושא היה סטיב ג'ובס, מנכ"ל אפל האגדי, שבצעירותו קיבל קורס קליגרפיה באוניברסיטה והושפע מהיופי של עולם האותיות והעיצוב. כשפיתח ג'ובס את מחשב המקינטוש, הוא הפך אותו למחשב גרפי שגופנים מעוצבים ומעוררי השראה ויופי תפסו בו מקום מרכזי.
קליגרפיה נקראת לעיתים בעברית "כתיבה תמה". מקור המילה בשפה היוונית: המלה "קאלוס" פירושה ביוונית "יופי" ו"גראפוס" היא ביוונית "כתיבה".
הנה הקליגרפיה הסינית הקדומה:
https://youtu.be/ppZWIwZsRdU
על קליגרף סיני שעשה לו שם בעולם (עברית):
https://youtu.be/d68TIY2_4H4
אוסף קליגרפיות מרהיבות:
https://youtu.be/zg7QLW0KrQw
מדריך מהיר לקליגרפיה מעשית:
https://youtu.be/Rnlha-GLL5s
קליגרפיה במחשב המקינטוש - הראשון שהעמיד במרכז את העיצוב הגרפי והקליגרפיה:
http://youtu.be/2B-XwPjn9YY?t=1m15s
יופייה של הקליגרפיה ביפאן (עברית):
http://youtu.be/cUI9PPeUCmI
והדגמה של הקליגרפיה היפנית (עברית):
http://youtu.be/geQtLi66W-A
