שלום,
נראה שכבר הכרתם את אאוריקה. בטח כבר גיליתם כאן דברים מדהימים, אולי כבר שאלתם שאלות וקיבלתם תשובות טובות.
נשמח לראות משהו מכם בספר האורחים שלנו: איזו מילה טובה, חוות דעת, עצה חכמה לשיפור או כל מה שיש לכם לספר לנו על אאוריקה, כפי שאתם חווים אותה.
»
«
מה זה ממוצע? ומהו חציון? ומה זה שכיח?
ממוצע, חציון ושכיח הם מספרים שמחושבים מתוך קבוצת מספרים:
הממוצע מתאר את "מרכז" קבוצת המספרים מבחינת גודלם. הוא המספר הדמיוני שכולם היו, אם הם היו שווים בגודלם.
החציון הוא המספר האמצעי בגודלו מבין קבוצת מספרים, כשהיא מסודרת לפי הסדר.
השכיח הוא המספר שניתן למצוא הכי הרבה בקבוצת מספרים.
אפילו שנראה אולי שמדובר בסתם עניינים של חישוב, ההבדלים בין המושגים הללו חשובים מאד. פעמים רבות מזכירים את הממוצע בהקשרים כלכליים. למשל כשמציינים שהשכר הממוצע במשק עלה. יש בכך נסיון לומר שאנשים מרוויחים שכר גבוה יותר, אבל מספיק שהמנהלים העלו את שכרם כדי "למשוך" את השכר הממוצע למעלה ולתת אשליה של עליה בשכר הכללי. מבט בחציון ייתן תמונה מדויקת יותר, כי שכרו של האדם האמצעי בין המשתכרים לא משתנה ומשקף טוב יותר את מצב השכר הכללי.
הנה "שיר הממוצע" שמסביר מהו הממוצע (Mean) והחציון (Median), שכיח (mode):
http://youtu.be/QH2obAPwfqk
עוד שיר שמלמד את המושגים הללו:
http://youtu.be/uydzT_WiRz4
על ההבדלים המתמטיים ביניהם:
http://youtu.be/onSebaCChTg
וסרטון שמסביר כמה הממוצע הוא דבר מטעה וכמה כדאי להכיר את החציון למשל (עברית):
http://youtu.be/cKHAfiqHwZc
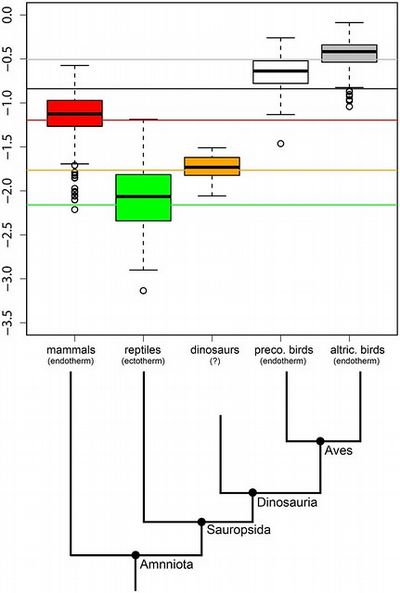מה עושים עם תרשים קופסה?
תרשים קופסה ("BoxPlot"), שנקרא גם תרשים תיבה, נותן סיכום חזותי של התפלגות נתונים בעזרת תיבה וקווים תוחמים מחוץ לתיבה, המכונים "שפמים".
תרשים הקופסה מספק 5 דברים על קבוצת הנתונים: המינימום, הרבעון התחתון, החציון, הרבעון העליון והמקסימום.
בתרשים מוצגים בצורה מרוכזת הערכים המרכזיים והפיזור של הנתונים:
#הרבעון התחתון והעליון - אלה גבולות התיבה שהם לרוב הרבעון התחתון והעליון. אלו ערכים שמתחת להם נמצאים 25% ו-75% מהנתונים.
חציון - הקו שבתוך התיבה. זהו החציון (Median), הערך האמצעי של הנתונים.
ערכי המינימום והמקסימום - ערכים שקל לזהות, כי הם מוצגים על ידי קצוות הקווים היוצאים מהקופסה ומכונים "שפמים" (whiskers). השפמים מיקומם בגבול הערכים הקיצוניים, שהם המינימום והמקסימום. ואגב, באנגלית קוראים לתרשימי קופסה גם "תרשימי קופסה ושפמים" (box and whisker plots).
נקודות בודדות מחוץ לטווח השפמים מסמנות ערכים חריגים. כלומר נתונים יוצאי דופן גבוהים או נמוכים במיוחד.
לדוגמה, בתרשים הקופסה יכולים להיות מוצגים ציוני מבחן של שתי כיתות: עבור כל כיתה יש "תיבה" אחת. ניתן לראות מצב בו בכיתה A החציון קצת גבוה מ-70, בעוד בכיתה B החציון הוא סביב 72. פיזור הציונים בכיתה B יכול להיות גדול יותר (התיבה ארוכה יותר וכך גם שפמי כיתה B הארוכים יותר - מה שמראה שהציונים בה מפוזרים על פני טווח רחב יותר). יכולה להיות גם נקודת עיגול מתחת לכיתה B, שמשמעותה היא למשל תלמיד שקיבל ציון חריג נמוך במיוחד לעומת שאר תלמידי כיתתו.
#יתרונות
תרשים קופסה מאפשר השוואה מהירה בין התפלגויות של קבוצות שונות. בגרף אחד אפשר לשים מספר "תיבות" זו ליד זו (כמו בדוגמת שתי הכיתות) ולהבין מיד באיזו קבוצה הערכים באופן כללי גבוהים יותר, איפה הפיזור רחב או צר יותר והאם יש חריגים.
זהו מידע שיהיה קשה לראות בגרפים פשוטים כמו גרף עמודות (שמציגים רק ממוצע או סכום ולא את פיזור הנתונים).
בנוסף, התרשים מספק הרבה מידע במבט מרוכז אחד: ממוצע או חציון, טווח בין-רבעוני (הקופסה), טווח כללי (השפמים) וחריגים, מבלי שנצטרך לראות כל נקודה ונקודה בנפרד.
#התאמה
תרשים הקופסה מתאים במיוחד עבור נתונים כמותיים, כאשר חשוב להבין את הפיזור והמגמה המרכזית שלהם, במיוחד בהשוואה בין כמה קבוצות.
למשל, בציוני מבחן של כמה כיתות שונות, בגבהים של זכרים מול נקבות או בהתפלגות הכנסות בערים שונות - בכל אלו מעניין לא רק מה הממוצע אלא איך הנתונים נפרשים סביבו.
תרשים קופסה שימושי גם בזיהוי ערכים חריגים שיכולים להיות חשובים. כמו, למשל, זיהוי ניסוי מדעי ש"תפס כיוון שונה" משאר התוצאות כי הוא חריג.
#דוגמאות
דוגמה מהחיים: דמיינו בית חולים שמשווה את זמן ההמתנה בחדר המיון בשלושה סניפים שונים. באמצעות תרשים קופסה, יוצג כל סניף בתיבה. אפשר לראות באיזה בית חולים זמן ההמתנה החציוני (חציון) קצר ביותר ובאיזה הפיזור גדול.
ייתכן שבבית חולים אחד לרוב ממתינים 10-20 דקות (תיבה קטנה), בעוד שבאחר הזמנים מגוונים ונפרשים מ-5 דקות ועד שעה (תיבה ושפמים גדולים יותר). מידע כזה עוזר לזהות איפה השירות עקבי ומהיר יותר.
עוד תרשים לדוגמה יכול להיות באמצעות Box Plot של ציוני שתי כיתות (כיתה A וכיתה B). הקו האדום בכל תיבה הוא החציון, הקופסה מראה את טווח הציונים האמצעי, והנקודות (כמו עיגול לבן) הן ערכים חריגים.
הנה הסבר של תרשים הקופסה:
https://youtu.be/Ck5HMTnvfw0
דוגמה שימושית לתרשים כזה:
https://youtu.be/b2C9I8HuCe4
חמשת הנקודות העיקריות בתרשים הקופסה:
https://youtu.be/E7ewAxluyt0
הנתונים שמראה תרשים קופסה:
https://youtu.be/EVm1NhGod1w
כך תקראו תרשים קופסה:
https://youtu.be/fHLhBnmwUM0
ותרשים קופסה בתוכנת אקסל:
https://youtu.be/f7rkB7c-zDw
חציון
ממוצע, חציון ושכיח הם מספרים שמחושבים מתוך קבוצת מספרים:
הממוצע מתאר את "מרכז" קבוצת המספרים מבחינת גודלם. הוא המספר הדמיוני שכולם היו, אם הם היו שווים בגודלם.
החציון הוא המספר האמצעי בגודלו מבין קבוצת מספרים, כשהיא מסודרת לפי הסדר.
השכיח הוא המספר שניתן למצוא הכי הרבה בקבוצת מספרים.
אפילו שנראה אולי שמדובר בסתם עניינים של חישוב, ההבדלים בין המושגים הללו חשובים מאד. פעמים רבות מזכירים את הממוצע בהקשרים כלכליים. למשל כשמציינים שהשכר הממוצע במשק עלה. יש בכך נסיון לומר שאנשים מרוויחים שכר גבוה יותר, אבל מספיק שהמנהלים העלו את שכרם כדי "למשוך" את השכר הממוצע למעלה ולתת אשליה של עליה בשכר הכללי. מבט בחציון ייתן תמונה מדויקת יותר, כי שכרו של האדם האמצעי בין המשתכרים לא משתנה ומשקף טוב יותר את מצב השכר הכללי.
הנה "שיר הממוצע" שמסביר מהו הממוצע (Mean) והחציון (Median), שכיח (mode):
http://youtu.be/QH2obAPwfqk
עוד שיר שמלמד את המושגים הללו:
http://youtu.be/uydzT_WiRz4
על ההבדלים המתמטיים ביניהם:
http://youtu.be/onSebaCChTg
וסרטון שמסביר כמה הממוצע הוא דבר מטעה וכמה כדאי להכיר את החציון למשל (עברית):
http://youtu.be/cKHAfiqHwZc
תרשים קופסה ("BoxPlot"), שנקרא גם תרשים תיבה, נותן סיכום חזותי של התפלגות נתונים בעזרת תיבה וקווים תוחמים מחוץ לתיבה, המכונים "שפמים".
תרשים הקופסה מספק 5 דברים על קבוצת הנתונים: המינימום, הרבעון התחתון, החציון, הרבעון העליון והמקסימום.
בתרשים מוצגים בצורה מרוכזת הערכים המרכזיים והפיזור של הנתונים:
#הרבעון התחתון והעליון - אלה גבולות התיבה שהם לרוב הרבעון התחתון והעליון. אלו ערכים שמתחת להם נמצאים 25% ו-75% מהנתונים.
חציון - הקו שבתוך התיבה. זהו החציון (Median), הערך האמצעי של הנתונים.
ערכי המינימום והמקסימום - ערכים שקל לזהות, כי הם מוצגים על ידי קצוות הקווים היוצאים מהקופסה ומכונים "שפמים" (whiskers). השפמים מיקומם בגבול הערכים הקיצוניים, שהם המינימום והמקסימום. ואגב, באנגלית קוראים לתרשימי קופסה גם "תרשימי קופסה ושפמים" (box and whisker plots).
נקודות בודדות מחוץ לטווח השפמים מסמנות ערכים חריגים. כלומר נתונים יוצאי דופן גבוהים או נמוכים במיוחד.
לדוגמה, בתרשים הקופסה יכולים להיות מוצגים ציוני מבחן של שתי כיתות: עבור כל כיתה יש "תיבה" אחת. ניתן לראות מצב בו בכיתה A החציון קצת גבוה מ-70, בעוד בכיתה B החציון הוא סביב 72. פיזור הציונים בכיתה B יכול להיות גדול יותר (התיבה ארוכה יותר וכך גם שפמי כיתה B הארוכים יותר - מה שמראה שהציונים בה מפוזרים על פני טווח רחב יותר). יכולה להיות גם נקודת עיגול מתחת לכיתה B, שמשמעותה היא למשל תלמיד שקיבל ציון חריג נמוך במיוחד לעומת שאר תלמידי כיתתו.
#יתרונות
תרשים קופסה מאפשר השוואה מהירה בין התפלגויות של קבוצות שונות. בגרף אחד אפשר לשים מספר "תיבות" זו ליד זו (כמו בדוגמת שתי הכיתות) ולהבין מיד באיזו קבוצה הערכים באופן כללי גבוהים יותר, איפה הפיזור רחב או צר יותר והאם יש חריגים.
זהו מידע שיהיה קשה לראות בגרפים פשוטים כמו גרף עמודות (שמציגים רק ממוצע או סכום ולא את פיזור הנתונים).
בנוסף, התרשים מספק הרבה מידע במבט מרוכז אחד: ממוצע או חציון, טווח בין-רבעוני (הקופסה), טווח כללי (השפמים) וחריגים, מבלי שנצטרך לראות כל נקודה ונקודה בנפרד.
#התאמה
תרשים הקופסה מתאים במיוחד עבור נתונים כמותיים, כאשר חשוב להבין את הפיזור והמגמה המרכזית שלהם, במיוחד בהשוואה בין כמה קבוצות.
למשל, בציוני מבחן של כמה כיתות שונות, בגבהים של זכרים מול נקבות או בהתפלגות הכנסות בערים שונות - בכל אלו מעניין לא רק מה הממוצע אלא איך הנתונים נפרשים סביבו.
תרשים קופסה שימושי גם בזיהוי ערכים חריגים שיכולים להיות חשובים. כמו, למשל, זיהוי ניסוי מדעי ש"תפס כיוון שונה" משאר התוצאות כי הוא חריג.
#דוגמאות
דוגמה מהחיים: דמיינו בית חולים שמשווה את זמן ההמתנה בחדר המיון בשלושה סניפים שונים. באמצעות תרשים קופסה, יוצג כל סניף בתיבה. אפשר לראות באיזה בית חולים זמן ההמתנה החציוני (חציון) קצר ביותר ובאיזה הפיזור גדול.
ייתכן שבבית חולים אחד לרוב ממתינים 10-20 דקות (תיבה קטנה), בעוד שבאחר הזמנים מגוונים ונפרשים מ-5 דקות ועד שעה (תיבה ושפמים גדולים יותר). מידע כזה עוזר לזהות איפה השירות עקבי ומהיר יותר.
עוד תרשים לדוגמה יכול להיות באמצעות Box Plot של ציוני שתי כיתות (כיתה A וכיתה B). הקו האדום בכל תיבה הוא החציון, הקופסה מראה את טווח הציונים האמצעי, והנקודות (כמו עיגול לבן) הן ערכים חריגים.
הנה הסבר של תרשים הקופסה:
https://youtu.be/Ck5HMTnvfw0
דוגמה שימושית לתרשים כזה:
https://youtu.be/b2C9I8HuCe4
חמשת הנקודות העיקריות בתרשים הקופסה:
https://youtu.be/E7ewAxluyt0
הנתונים שמראה תרשים קופסה:
https://youtu.be/EVm1NhGod1w
כך תקראו תרשים קופסה:
https://youtu.be/fHLhBnmwUM0
ותרשים קופסה בתוכנת אקסל:
https://youtu.be/f7rkB7c-zDw
