שלום,
נראה שכבר הכרתם את אאוריקה. בטח כבר גיליתם כאן דברים מדהימים, אולי כבר שאלתם שאלות וקיבלתם תשובות טובות.
נשמח לראות משהו מכם בספר האורחים שלנו: איזו מילה טובה, חוות דעת, עצה חכמה לשיפור או כל מה שיש לכם לספר לנו על אאוריקה, כפי שאתם חווים אותה.
»
«
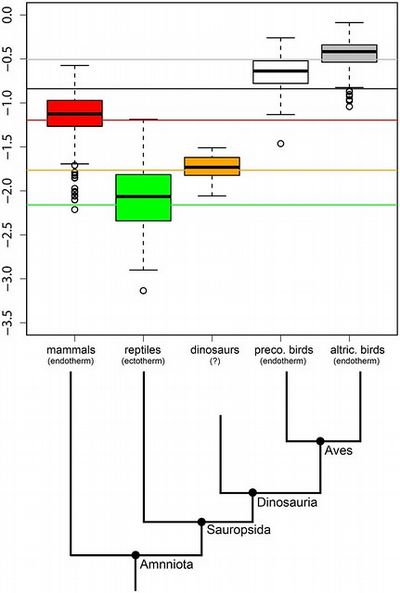 מה עושים עם תרשים קופסה?
מה עושים עם תרשים קופסה?
תרשים קופסה ("BoxPlot"), שנקרא גם תרשים תיבה, נותן סיכום חזותי של התפלגות נתונים בעזרת תיבה וקווים תוחמים מחוץ לתיבה, המכונים "שפמים".
תרשים הקופסה מספק 5 דברים על קבוצת הנתונים: המינימום, הרבעון התחתון, החציון, הרבעון העליון והמקסימום.
בתרשים מוצגים בצורה מרוכזת הערכים המרכזיים והפיזור של הנתונים:
#הרבעון התחתון והעליון - אלה גבולות התיבה שהם לרוב הרבעון התחתון והעליון. אלו ערכים שמתחת להם נמצאים 25% ו-75% מהנתונים.
חציון - הקו שבתוך התיבה. זהו החציון (Median), הערך האמצעי של הנתונים.
ערכי המינימום והמקסימום - ערכים שקל לזהות, כי הם מוצגים על ידי קצוות הקווים היוצאים מהקופסה ומכונים "שפמים" (whiskers). השפמים מיקומם בגבול הערכים הקיצוניים, שהם המינימום והמקסימום. ואגב, באנגלית קוראים לתרשימי קופסה גם "תרשימי קופסה ושפמים" (box and whisker plots).
נקודות בודדות מחוץ לטווח השפמים מסמנות ערכים חריגים. כלומר נתונים יוצאי דופן גבוהים או נמוכים במיוחד.
לדוגמה, בתרשים הקופסה יכולים להיות מוצגים ציוני מבחן של שתי כיתות: עבור כל כיתה יש "תיבה" אחת. ניתן לראות מצב בו בכיתה A החציון קצת גבוה מ-70, בעוד בכיתה B החציון הוא סביב 72. פיזור הציונים בכיתה B יכול להיות גדול יותר (התיבה ארוכה יותר וכך גם שפמי כיתה B הארוכים יותר - מה שמראה שהציונים בה מפוזרים על פני טווח רחב יותר). יכולה להיות גם נקודת עיגול מתחת לכיתה B, שמשמעותה היא למשל תלמיד שקיבל ציון חריג נמוך במיוחד לעומת שאר תלמידי כיתתו.
#יתרונות
תרשים קופסה מאפשר השוואה מהירה בין התפלגויות של קבוצות שונות. בגרף אחד אפשר לשים מספר "תיבות" זו ליד זו (כמו בדוגמת שתי הכיתות) ולהבין מיד באיזו קבוצה הערכים באופן כללי גבוהים יותר, איפה הפיזור רחב או צר יותר והאם יש חריגים.
זהו מידע שיהיה קשה לראות בגרפים פשוטים כמו גרף עמודות (שמציגים רק ממוצע או סכום ולא את פיזור הנתונים).
בנוסף, התרשים מספק הרבה מידע במבט מרוכז אחד: ממוצע או חציון, טווח בין-רבעוני (הקופסה), טווח כללי (השפמים) וחריגים, מבלי שנצטרך לראות כל נקודה ונקודה בנפרד.
#התאמה
תרשים הקופסה מתאים במיוחד עבור נתונים כמותיים, כאשר חשוב להבין את הפיזור והמגמה המרכזית שלהם, במיוחד בהשוואה בין כמה קבוצות.
למשל, בציוני מבחן של כמה כיתות שונות, בגבהים של זכרים מול נקבות או בהתפלגות הכנסות בערים שונות - בכל אלו מעניין לא רק מה הממוצע אלא איך הנתונים נפרשים סביבו.
תרשים קופסה שימושי גם בזיהוי ערכים חריגים שיכולים להיות חשובים. כמו, למשל, זיהוי ניסוי מדעי ש"תפס כיוון שונה" משאר התוצאות כי הוא חריג.
#דוגמאות
דוגמה מהחיים: דמיינו בית חולים שמשווה את זמן ההמתנה בחדר המיון בשלושה סניפים שונים. באמצעות תרשים קופסה, יוצג כל סניף בתיבה. אפשר לראות באיזה בית חולים זמן ההמתנה החציוני (חציון) קצר ביותר ובאיזה הפיזור גדול.
ייתכן שבבית חולים אחד לרוב ממתינים 10-20 דקות (תיבה קטנה), בעוד שבאחר הזמנים מגוונים ונפרשים מ-5 דקות ועד שעה (תיבה ושפמים גדולים יותר). מידע כזה עוזר לזהות איפה השירות עקבי ומהיר יותר.
עוד תרשים לדוגמה יכול להיות באמצעות Box Plot של ציוני שתי כיתות (כיתה A וכיתה B). הקו האדום בכל תיבה הוא החציון, הקופסה מראה את טווח הציונים האמצעי, והנקודות (כמו עיגול לבן) הן ערכים חריגים.
הנה הסבר של תרשים הקופסה:
https://youtu.be/Ck5HMTnvfw0
דוגמה שימושית לתרשים כזה:
https://youtu.be/b2C9I8HuCe4
חמשת הנקודות העיקריות בתרשים הקופסה:
https://youtu.be/E7ewAxluyt0
הנתונים שמראה תרשים קופסה:
https://youtu.be/EVm1NhGod1w
כך תקראו תרשים קופסה:
https://youtu.be/fHLhBnmwUM0
ותרשים קופסה בתוכנת אקסל:
https://youtu.be/f7rkB7c-zDw
 מה זה גרף ולמה צריך גרפים?
מה זה גרף ולמה צריך גרפים?
גְּרָף (Graph Data), או גרף נתונים, הוא תיאור שבדרך כלל הוא דו-ממדי של מספר פרטי מידע המקושרים ביניהם על ידי יחסים כלשהם.
הגרף ישמש בדרך כלל להצגה חזותית של מידע כמותי. הוא מאפשר השוואה של הפריטים השונים זה לזה, בעזרת יחידות המידה שבדרך כלל מוצגות על הציר או על שני צירי הגרף. כי גם אם גרפים עתירי נתונים יוצגו לעתים עם מערכת צירים תלת-ממדית, בדרך כלל הם יוצגו בגרפים המבוססים על מערכת צירים דו-ממדית.
הציר האופקי, הציר שממש כמו האופק שאליו אנו מביטים נמתח לרוחב, יציג בדרך כלל את המשתנה. אם למשל נציג גרף של פופולריות של מוצר לאורך תקופה מסוימת, אז הציר האופקי יציג את הזמן, למשל את החודשים בשנה האחרונה.
הציר האנכי, העומד, יציג את הפונקציה. למשל בגרף של פופולריות המוצר בשנה האחרונה הציר הזה יציג את הפופולריות שלו, הפונקציה של המשתנה - כמה המוצר נמכר, או מה אחוז הנשאלים שאהבו את המוצר בסקר החודשי.
#למה צריך את זה?
גדולתו של הגרף היא בייצוג ויזואלי והשוואתי, באופן מופשט וללא מידע מיותר. כל זה לגבי קבוצת הפריטים או הנתונים, כשכולם מקושרים ביניהם באופן כלשהו.
יתרונם הגדול של הגרפים הוא בקלות ובמהירות של קליטת המידע מהם. גרף טוב יאפשר זיהוי מהיר של הקשר בין הנתונים והיחסים ביניהם, לעתים גם כולל המגמות שניתן לזהות בהם והחריגות שבין הנתונים.
#סוגי גרפים
ישנם כמה סוגי גרפים, כשלכל סוג יש יתרונות משלו ושימושים מתאימים לסוג המידע שהוא מציג היטב לצרכי ויזואליזציה של נתונים.
הגרפים הבולטים, השכיחים והשימושיים ביותר הם גרף עמודות, גרף קו, גרף עוגה, היסטוגרמה, גרף פיזור, תרשים קופסה (Box Plot), גרף בועות, גרף רציף, גרף נרות יפניים (גרף קו המציג את המדידות בניתוח טכני באופן משוכלל יותר מנקודות על הקו) ומפת חום (Heatmap) שהיא מעט שונה אבל נחשבת גם היא לסוג של גרף.
למחקר תאורטי נרחב זכו הגרפים במסגרת תורת הגרפים. ישנם סוגי גרפים שונים. להיכרות איתם ראו את תגית "סוגי גרפים".
הנה הסבר לילדים על מה זה גרף:
https://youtu.be/LW7I0Skjaew
כמה מסוגי הגרפים שמשתמשים בהם:
https://youtu.be/bmY28wdGL9M
איך יודעים באיזה גרף להשתמש בכל הקשר?
https://youtu.be/o7F-tbBl_hA
גרף נתונים בקו שמדגים את השינויים לאורך זמן (עברית):
https://youtu.be/siBhC7scAdQ
כך אפשר לזהות הטעיה באמצעות גרף (מתורגם):
https://youtu.be/E91bGT9BjYk
וגרף הנרות היפניים בעולם המסחר במניות (עברית):
https://youtu.be/FPZbtNtbMtc?long=yes
תרשים קופסה

תרשים קופסה ("BoxPlot"), שנקרא גם תרשים תיבה, נותן סיכום חזותי של התפלגות נתונים בעזרת תיבה וקווים תוחמים מחוץ לתיבה, המכונים "שפמים".
תרשים הקופסה מספק 5 דברים על קבוצת הנתונים: המינימום, הרבעון התחתון, החציון, הרבעון העליון והמקסימום.
בתרשים מוצגים בצורה מרוכזת הערכים המרכזיים והפיזור של הנתונים:
#הרבעון התחתון והעליון - אלה גבולות התיבה שהם לרוב הרבעון התחתון והעליון. אלו ערכים שמתחת להם נמצאים 25% ו-75% מהנתונים.
חציון - הקו שבתוך התיבה. זהו החציון (Median), הערך האמצעי של הנתונים.
ערכי המינימום והמקסימום - ערכים שקל לזהות, כי הם מוצגים על ידי קצוות הקווים היוצאים מהקופסה ומכונים "שפמים" (whiskers). השפמים מיקומם בגבול הערכים הקיצוניים, שהם המינימום והמקסימום. ואגב, באנגלית קוראים לתרשימי קופסה גם "תרשימי קופסה ושפמים" (box and whisker plots).
נקודות בודדות מחוץ לטווח השפמים מסמנות ערכים חריגים. כלומר נתונים יוצאי דופן גבוהים או נמוכים במיוחד.
לדוגמה, בתרשים הקופסה יכולים להיות מוצגים ציוני מבחן של שתי כיתות: עבור כל כיתה יש "תיבה" אחת. ניתן לראות מצב בו בכיתה A החציון קצת גבוה מ-70, בעוד בכיתה B החציון הוא סביב 72. פיזור הציונים בכיתה B יכול להיות גדול יותר (התיבה ארוכה יותר וכך גם שפמי כיתה B הארוכים יותר - מה שמראה שהציונים בה מפוזרים על פני טווח רחב יותר). יכולה להיות גם נקודת עיגול מתחת לכיתה B, שמשמעותה היא למשל תלמיד שקיבל ציון חריג נמוך במיוחד לעומת שאר תלמידי כיתתו.
#יתרונות
תרשים קופסה מאפשר השוואה מהירה בין התפלגויות של קבוצות שונות. בגרף אחד אפשר לשים מספר "תיבות" זו ליד זו (כמו בדוגמת שתי הכיתות) ולהבין מיד באיזו קבוצה הערכים באופן כללי גבוהים יותר, איפה הפיזור רחב או צר יותר והאם יש חריגים.
זהו מידע שיהיה קשה לראות בגרפים פשוטים כמו גרף עמודות (שמציגים רק ממוצע או סכום ולא את פיזור הנתונים).
בנוסף, התרשים מספק הרבה מידע במבט מרוכז אחד: ממוצע או חציון, טווח בין-רבעוני (הקופסה), טווח כללי (השפמים) וחריגים, מבלי שנצטרך לראות כל נקודה ונקודה בנפרד.
#התאמה
תרשים הקופסה מתאים במיוחד עבור נתונים כמותיים, כאשר חשוב להבין את הפיזור והמגמה המרכזית שלהם, במיוחד בהשוואה בין כמה קבוצות.
למשל, בציוני מבחן של כמה כיתות שונות, בגבהים של זכרים מול נקבות או בהתפלגות הכנסות בערים שונות - בכל אלו מעניין לא רק מה הממוצע אלא איך הנתונים נפרשים סביבו.
תרשים קופסה שימושי גם בזיהוי ערכים חריגים שיכולים להיות חשובים. כמו, למשל, זיהוי ניסוי מדעי ש"תפס כיוון שונה" משאר התוצאות כי הוא חריג.
#דוגמאות
דוגמה מהחיים: דמיינו בית חולים שמשווה את זמן ההמתנה בחדר המיון בשלושה סניפים שונים. באמצעות תרשים קופסה, יוצג כל סניף בתיבה. אפשר לראות באיזה בית חולים זמן ההמתנה החציוני (חציון) קצר ביותר ובאיזה הפיזור גדול.
ייתכן שבבית חולים אחד לרוב ממתינים 10-20 דקות (תיבה קטנה), בעוד שבאחר הזמנים מגוונים ונפרשים מ-5 דקות ועד שעה (תיבה ושפמים גדולים יותר). מידע כזה עוזר לזהות איפה השירות עקבי ומהיר יותר.
עוד תרשים לדוגמה יכול להיות באמצעות Box Plot של ציוני שתי כיתות (כיתה A וכיתה B). הקו האדום בכל תיבה הוא החציון, הקופסה מראה את טווח הציונים האמצעי, והנקודות (כמו עיגול לבן) הן ערכים חריגים.
הנה הסבר של תרשים הקופסה:
https://youtu.be/Ck5HMTnvfw0
דוגמה שימושית לתרשים כזה:
https://youtu.be/b2C9I8HuCe4
חמשת הנקודות העיקריות בתרשים הקופסה:
https://youtu.be/E7ewAxluyt0
הנתונים שמראה תרשים קופסה:
https://youtu.be/EVm1NhGod1w
כך תקראו תרשים קופסה:
https://youtu.be/fHLhBnmwUM0
ותרשים קופסה בתוכנת אקסל:
https://youtu.be/f7rkB7c-zDw

גְּרָף (Graph Data), או גרף נתונים, הוא תיאור שבדרך כלל הוא דו-ממדי של מספר פרטי מידע המקושרים ביניהם על ידי יחסים כלשהם.
הגרף ישמש בדרך כלל להצגה חזותית של מידע כמותי. הוא מאפשר השוואה של הפריטים השונים זה לזה, בעזרת יחידות המידה שבדרך כלל מוצגות על הציר או על שני צירי הגרף. כי גם אם גרפים עתירי נתונים יוצגו לעתים עם מערכת צירים תלת-ממדית, בדרך כלל הם יוצגו בגרפים המבוססים על מערכת צירים דו-ממדית.
הציר האופקי, הציר שממש כמו האופק שאליו אנו מביטים נמתח לרוחב, יציג בדרך כלל את המשתנה. אם למשל נציג גרף של פופולריות של מוצר לאורך תקופה מסוימת, אז הציר האופקי יציג את הזמן, למשל את החודשים בשנה האחרונה.
הציר האנכי, העומד, יציג את הפונקציה. למשל בגרף של פופולריות המוצר בשנה האחרונה הציר הזה יציג את הפופולריות שלו, הפונקציה של המשתנה - כמה המוצר נמכר, או מה אחוז הנשאלים שאהבו את המוצר בסקר החודשי.
#למה צריך את זה?
גדולתו של הגרף היא בייצוג ויזואלי והשוואתי, באופן מופשט וללא מידע מיותר. כל זה לגבי קבוצת הפריטים או הנתונים, כשכולם מקושרים ביניהם באופן כלשהו.
יתרונם הגדול של הגרפים הוא בקלות ובמהירות של קליטת המידע מהם. גרף טוב יאפשר זיהוי מהיר של הקשר בין הנתונים והיחסים ביניהם, לעתים גם כולל המגמות שניתן לזהות בהם והחריגות שבין הנתונים.
#סוגי גרפים
ישנם כמה סוגי גרפים, כשלכל סוג יש יתרונות משלו ושימושים מתאימים לסוג המידע שהוא מציג היטב לצרכי ויזואליזציה של נתונים.
הגרפים הבולטים, השכיחים והשימושיים ביותר הם גרף עמודות, גרף קו, גרף עוגה, היסטוגרמה, גרף פיזור, תרשים קופסה (Box Plot), גרף בועות, גרף רציף, גרף נרות יפניים (גרף קו המציג את המדידות בניתוח טכני באופן משוכלל יותר מנקודות על הקו) ומפת חום (Heatmap) שהיא מעט שונה אבל נחשבת גם היא לסוג של גרף.
למחקר תאורטי נרחב זכו הגרפים במסגרת תורת הגרפים. ישנם סוגי גרפים שונים. להיכרות איתם ראו את תגית "סוגי גרפים".
הנה הסבר לילדים על מה זה גרף:
https://youtu.be/LW7I0Skjaew
כמה מסוגי הגרפים שמשתמשים בהם:
https://youtu.be/bmY28wdGL9M
איך יודעים באיזה גרף להשתמש בכל הקשר?
https://youtu.be/o7F-tbBl_hA
גרף נתונים בקו שמדגים את השינויים לאורך זמן (עברית):
https://youtu.be/siBhC7scAdQ
כך אפשר לזהות הטעיה באמצעות גרף (מתורגם):
https://youtu.be/E91bGT9BjYk
וגרף הנרות היפניים בעולם המסחר במניות (עברית):
https://youtu.be/FPZbtNtbMtc?long=yes
