שלום,
נראה שכבר הכרתם את אאוריקה. בטח כבר גיליתם כאן דברים מדהימים, אולי כבר שאלתם שאלות וקיבלתם תשובות טובות.
נשמח לראות משהו מכם בספר האורחים שלנו: איזו מילה טובה, חוות דעת, עצה חכמה לשיפור או כל מה שיש לכם לספר לנו על אאוריקה, כפי שאתם חווים אותה.
»
«
מהי הגאומטריה של מנדלברוט?
בנואה מנדלברוט היה מתמטיקאי שמצא שיש צורות רבות שכל חלק שלהן הוא כמו השלם, או מזכיר אותו. מדידה של שטח הפנים של צורות כאלה תלוייה ביכולת שלנו לבחון אותו, מכיוון שככל שנתקרב אל העצם, נגלה חספוס הולך וגובר, שיגדיל את שטח הפנים.
מנדלברוט מצא שכלל מתמטי פשוט, או נוסחה פשוטה, יכולים להגדיר מצוין את העצם שנראה שאין בו חוקיות או היגיון כלשהם.
אגב, בנואה מנדלברוט עצמו מעדיף את המונח "חספוס" ולא אי-יציבות או אי-סדר, מכיוון שהוא רואה סדר בכל דבר ואין בעיניו שום דבר שאין בו סדר מסוים. להוכחה, המילה "פרקטל" שהוא בחר לתיאור של המחוספס והשבור באה מהמילה הלטינית פרקטוס (fractus), שפירושה "שבור".
למשל בכרובית הוא רואה גם תחכום וגם פשטות. אותם קונוסים שאנו רואים בברוקולי, חוזרים גם אם נביט בחלק מקונוס כזה ויחזרו שוב ושוב בכל קנה מידה שנביט בו. כך יהיה גם בעננים, בקווי חוף עם מפרצים בגדלים (מפיורדים עצומים ועד מפרצונים בגוגל מילימטרים), עצים (בהם עורקי העלה נראים כענפים וענפי העץ דומים לעצים) ועוד המון צורות שהן לכאורה אקראיות ולא בנויות בסדר של ממש, אבל כשנביט בחלק מהם נראה בגדלים שונים, תבנית דומה לזו שראינו בעצם המלא.
איך זה מסתדר? - ובכן, בכולם יש מרכיב שניתן למצוא והוא "הדמיון העצמי" (Self similarity), שבו אותה צורה חוזרת שוב ושוב, ככל שנתקרב. ומסתבר שאותה צורה שבה ענפים יוצאים מענפים בעץ, היא גם הצורה של צינורות הדם בגופנו, נימי העלים של העץ, נהרות על פני כדור הארץ וכן הלאה. מסתבר שהטבע עושה שימוש בחוק זהה להמון מקרים שאינם קשורים זה בזה ושכביכול אין בהם שום סדר הגיוני.
ל"דמיון העצמי" מנדלברוט קרא "פרקטל". הוא גם הבין שניתן לעבוד עם הפרקטלים הפוך ולהשתמש בסדרה של חוקים מתמטיים פשוטים, כדי לייצר צורות כאלה. בסוף שנות ה-50 הוא השתמש במחשב כדי לייצר צורות כאלה. הוא עשה מהפכה של ממש בגאומטריה, שכן הוא החל לקרב אותה לעולם הטבע.
אם קודם לפרקטלים לא סייעה הגאומטריה לתאר את הצורות של גורמים בטבע, כמו הרים, עננים, עצים, ירקות וקווי חוף, הרי שהפרקטל, שמסייע למצוא סדר בדפוסים מורכבים ביותר, שינה את זה והראה את הסדר המתמטי שבו מתנהל הטבע והעולם הכאוטי. או במילים שלו כפי שכתב בהקדמת ספרו "עננים הם לא כדורים, הרים אינם בעלי צורה של חרוט, קו החוף לא עשוי ממעגלים, קליפת העץ איננה חלקה והברק אינו מתקדם בקו ישר".
בחייו סבל מנדלברוט לא מעט בשל הפרקטלים. הממסד המתמטי ממש נידה אותו בשל ההתעסקות בתמונות, שלא יאה למתמטיקאי רציני. מי שהצילה אותו מחוסר תעסוקה הייתה חברת IBM, שלא זו בלבד שהעסיקה אותו במרכז המחקר שלה, אלא אף נתנה לו לעשות כרצונו. בעזרת חוק רקורסיבי פשוט מאוד הוא מצליח עתה לייצר תמונות בעלות מורכבות הולכת וגדלה, בה רואים ברמות שונות, כאמור, צורות דומות.
גם הציבור הרחב מתחיל להתחבר לרעיונות שלו, שבניגוד לרעיונות מתמטיים רגילים, קל להבינם. מה עוד שניתן היה לראותם לפתע, בתוצרי מחשב מודפסים. את הצד הגרפי של הפרקטלים ניתן היה גם לחקור וליישם באדריכלות, בעיצוב מוצר ובתעשיות שונות.
וכך זוכה מי שכילד בן 12 הפך לפליט פולני בצרפת ולימד את עצמו מתמטיקה לבדו, הוא זוכה בשלב מסוים בציבור לכינוי "כוכב הרוק של המתמטיקה". כי גם אם רעיונותיו על הפרקטלים עדיין לא מתקבלים אצל הקהילה המדעית, מעל ראשם הוא הופך די מהר לאחד המתמטיקאים המשפיעים בהיסטוריה.
הנה סרטון שמסביר זאת היטב:
http://youtu.be/Dm-zy5f4qIo
הדמיון העצמי של פרקטל:
http://youtu.be/9G6uO7ZHtK8
הסבריו של מנדלברוט עצמו:
http://youtu.be/pDajf3PXpNI
ודוגמאות שונות לסט מנדלברוט, שמערב סיבוכיות, הרמוניה ויופי בשימוש בנוסחאות פשוטות:
http://youtu.be/G_GBwuYuOOs
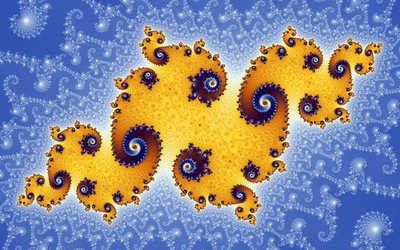מהי קבוצת מנדלברוט?
חבורת מנדלברוט, קבוצת מנדלברוט או סט מנדלברוט, הם שמות לצורות שחוזרות על עצמן ללא סוף. אלה צורות עם דמיון עצמי, כלומר כל חלק שלהן דומה לשלם. במילים אחרות, בכל צורה כזו נוכל לראות את הצורה בחלקים השונים שבה וכך שוב ושוב כשנביט אל חלקי החלקים הללו, ככל שנביט פנימה. כשבוחנים פרקטל בזום, או בזכוכית מגדלת, מגלים את אותו הדפוס בקנה מידה קטן וכך זה הולך וקטן לקני מידה הולכים וקטנים, עד אינסוף.
את הצורות המופלאות הללו יצר המתמטיקאי הצרפתי בנואה מנדלברוט, על פי פרקטלים של ג'וליה, מתמטיקאי שקדם לו. המעניין הוא שאלה צורות המערבות סיבוכיות, הרמוניה ויופי, אבל למעשה משתמשות בנוסחה מתמטית פשוטה. משהו כמו Zn = Z + C^2 כשכל מספר ב-C ייתן צורה שונה לחלוטין.
והתגלית המעניינת היא שהצורות הללו נראות כמו הרבה דברים שאנו מכירים מהטבע. בסטים הללו נוצר מגוון אדיר של צורות קסומות, המזכירות איים קסומים ודימיוניים, קישוטים בארוקיים מדומים, עצים מרהיבים, חופים כפי שהן נראים ממעוף הציפור וכדומה. זו הסיבה שכיום עושים בסט מנדלברוט שימוש ביצירת נופים ועולמות מדומים במשחקי מחשב, בעולמות מדומים, בסרטים ובסימולציות שונות.
הנה הפרקטלים שבטבע וכיצד ניתן ליצור אותם בעצמנו:
http://youtu.be/XwWyTts06tU
הבה נתקרב עוד ועוד לפרקטל הכי מוכר מקבוצת מנדלברוט:
http://youtu.be/gEw8xpb1aRA
הסבר על הפרקטלים של מנדלברוט:
http://youtu.be/STSS3_cVauk
ושיר על הסט של מנדלברוט:
http://youtu.be/ES-yKOYaXq0
מהו פרדוקס קו החוף?
האם ניסיתם פעם למדוד אורכו של משהו? - זה לא אמור להיות קשה, נכון?
אבל חופים הם לפעמים בעיה של ממש למודדים.. וזה לא רק לפעמים - חופים הם בעיקרון בעיה למודדים! - הם מדגימים היטב את הרעיון שהמימד הוא לא מוחלט אלא תלוי בסקלה שבה אנו מסתכלים או מודדים.
למה אנו מכוונים?
כשאנו מודדים את אורכו של קו חוף, נגלה תופעה מאד מוזרה - ככל נתקרב לקו החוף, יילך אורכו ויגדל. פרדוקס קו החוף הוא ההבחנה המדעית שאין לנו יכולת למדוד באמת את אורכו של קו חוף. כי ככל שהסרגל שלנו יהיה קטן יותר, ניאלץ נמדוד את החוף מקרוב יותר, הפיתולים שלו יימדדו ויאריכו את האורך הנמדד של קו החוף.
במילים אחרות - קו החוף יילך ויגדל, ככל שנמדוד אותו ביחידות קטנות יותר. למה זה קורה? - כי סרגל הוא ישר ולא ניתן להשתמש בו כדי למדוד פיתולים הקטנים יותר מאורכו. לפיכך, ככל שהסרגל הוא קטן יותר, נוכל למדוד אתו בתוך הפיתולים ואורכו הסופי של החוף יגדל משמעותית.
כמובן שפרדוקס קו החוף לא מדבר רק על חופים, אלא על כל דבר שאינו ישר. נוכל לראות תופעה דומה גם במדידה של אורך העיגול, של פני השטח של אלמוג, של מידות המוח וכדומה.
פרדוקס קו החוף הוא אחת הדוגמאות שהציג במחקריו המתמטיקאי בנואה מנדלברוט. הוא הדגים בעזרתו כיצד יכול השימוש בפרקטלים, אותם יצורים מתמטיים של דמיון עצמי, שמכילים את עצמם, לסייע בתיאור תופעות טבע, במקרה הזה את מבנה קו החוף. קראו עליהם באאוריקה בתגית "פרקטלים".
הנה סרטון הסבר לפרדוקס קו החוף:
https://youtu.be/kFjq8PX6F7I
והבעיה שמוצגת היטב במדידת אורכם של חופי אוסטרליה:
http://youtu.be/I_rw-AJqpCM
בנואה מנדלברוט
בנואה מנדלברוט היה מתמטיקאי שמצא שיש צורות רבות שכל חלק שלהן הוא כמו השלם, או מזכיר אותו. מדידה של שטח הפנים של צורות כאלה תלוייה ביכולת שלנו לבחון אותו, מכיוון שככל שנתקרב אל העצם, נגלה חספוס הולך וגובר, שיגדיל את שטח הפנים.
מנדלברוט מצא שכלל מתמטי פשוט, או נוסחה פשוטה, יכולים להגדיר מצוין את העצם שנראה שאין בו חוקיות או היגיון כלשהם.
אגב, בנואה מנדלברוט עצמו מעדיף את המונח "חספוס" ולא אי-יציבות או אי-סדר, מכיוון שהוא רואה סדר בכל דבר ואין בעיניו שום דבר שאין בו סדר מסוים. להוכחה, המילה "פרקטל" שהוא בחר לתיאור של המחוספס והשבור באה מהמילה הלטינית פרקטוס (fractus), שפירושה "שבור".
למשל בכרובית הוא רואה גם תחכום וגם פשטות. אותם קונוסים שאנו רואים בברוקולי, חוזרים גם אם נביט בחלק מקונוס כזה ויחזרו שוב ושוב בכל קנה מידה שנביט בו. כך יהיה גם בעננים, בקווי חוף עם מפרצים בגדלים (מפיורדים עצומים ועד מפרצונים בגוגל מילימטרים), עצים (בהם עורקי העלה נראים כענפים וענפי העץ דומים לעצים) ועוד המון צורות שהן לכאורה אקראיות ולא בנויות בסדר של ממש, אבל כשנביט בחלק מהם נראה בגדלים שונים, תבנית דומה לזו שראינו בעצם המלא.
איך זה מסתדר? - ובכן, בכולם יש מרכיב שניתן למצוא והוא "הדמיון העצמי" (Self similarity), שבו אותה צורה חוזרת שוב ושוב, ככל שנתקרב. ומסתבר שאותה צורה שבה ענפים יוצאים מענפים בעץ, היא גם הצורה של צינורות הדם בגופנו, נימי העלים של העץ, נהרות על פני כדור הארץ וכן הלאה. מסתבר שהטבע עושה שימוש בחוק זהה להמון מקרים שאינם קשורים זה בזה ושכביכול אין בהם שום סדר הגיוני.
ל"דמיון העצמי" מנדלברוט קרא "פרקטל". הוא גם הבין שניתן לעבוד עם הפרקטלים הפוך ולהשתמש בסדרה של חוקים מתמטיים פשוטים, כדי לייצר צורות כאלה. בסוף שנות ה-50 הוא השתמש במחשב כדי לייצר צורות כאלה. הוא עשה מהפכה של ממש בגאומטריה, שכן הוא החל לקרב אותה לעולם הטבע.
אם קודם לפרקטלים לא סייעה הגאומטריה לתאר את הצורות של גורמים בטבע, כמו הרים, עננים, עצים, ירקות וקווי חוף, הרי שהפרקטל, שמסייע למצוא סדר בדפוסים מורכבים ביותר, שינה את זה והראה את הסדר המתמטי שבו מתנהל הטבע והעולם הכאוטי. או במילים שלו כפי שכתב בהקדמת ספרו "עננים הם לא כדורים, הרים אינם בעלי צורה של חרוט, קו החוף לא עשוי ממעגלים, קליפת העץ איננה חלקה והברק אינו מתקדם בקו ישר".
בחייו סבל מנדלברוט לא מעט בשל הפרקטלים. הממסד המתמטי ממש נידה אותו בשל ההתעסקות בתמונות, שלא יאה למתמטיקאי רציני. מי שהצילה אותו מחוסר תעסוקה הייתה חברת IBM, שלא זו בלבד שהעסיקה אותו במרכז המחקר שלה, אלא אף נתנה לו לעשות כרצונו. בעזרת חוק רקורסיבי פשוט מאוד הוא מצליח עתה לייצר תמונות בעלות מורכבות הולכת וגדלה, בה רואים ברמות שונות, כאמור, צורות דומות.
גם הציבור הרחב מתחיל להתחבר לרעיונות שלו, שבניגוד לרעיונות מתמטיים רגילים, קל להבינם. מה עוד שניתן היה לראותם לפתע, בתוצרי מחשב מודפסים. את הצד הגרפי של הפרקטלים ניתן היה גם לחקור וליישם באדריכלות, בעיצוב מוצר ובתעשיות שונות.
וכך זוכה מי שכילד בן 12 הפך לפליט פולני בצרפת ולימד את עצמו מתמטיקה לבדו, הוא זוכה בשלב מסוים בציבור לכינוי "כוכב הרוק של המתמטיקה". כי גם אם רעיונותיו על הפרקטלים עדיין לא מתקבלים אצל הקהילה המדעית, מעל ראשם הוא הופך די מהר לאחד המתמטיקאים המשפיעים בהיסטוריה.
הנה סרטון שמסביר זאת היטב:
http://youtu.be/Dm-zy5f4qIo
הדמיון העצמי של פרקטל:
http://youtu.be/9G6uO7ZHtK8
הסבריו של מנדלברוט עצמו:
http://youtu.be/pDajf3PXpNI
ודוגמאות שונות לסט מנדלברוט, שמערב סיבוכיות, הרמוניה ויופי בשימוש בנוסחאות פשוטות:
http://youtu.be/G_GBwuYuOOs
חבורת מנדלברוט, קבוצת מנדלברוט או סט מנדלברוט, הם שמות לצורות שחוזרות על עצמן ללא סוף. אלה צורות עם דמיון עצמי, כלומר כל חלק שלהן דומה לשלם. במילים אחרות, בכל צורה כזו נוכל לראות את הצורה בחלקים השונים שבה וכך שוב ושוב כשנביט אל חלקי החלקים הללו, ככל שנביט פנימה. כשבוחנים פרקטל בזום, או בזכוכית מגדלת, מגלים את אותו הדפוס בקנה מידה קטן וכך זה הולך וקטן לקני מידה הולכים וקטנים, עד אינסוף.
את הצורות המופלאות הללו יצר המתמטיקאי הצרפתי בנואה מנדלברוט, על פי פרקטלים של ג'וליה, מתמטיקאי שקדם לו. המעניין הוא שאלה צורות המערבות סיבוכיות, הרמוניה ויופי, אבל למעשה משתמשות בנוסחה מתמטית פשוטה. משהו כמו Zn = Z + C^2 כשכל מספר ב-C ייתן צורה שונה לחלוטין.
והתגלית המעניינת היא שהצורות הללו נראות כמו הרבה דברים שאנו מכירים מהטבע. בסטים הללו נוצר מגוון אדיר של צורות קסומות, המזכירות איים קסומים ודימיוניים, קישוטים בארוקיים מדומים, עצים מרהיבים, חופים כפי שהן נראים ממעוף הציפור וכדומה. זו הסיבה שכיום עושים בסט מנדלברוט שימוש ביצירת נופים ועולמות מדומים במשחקי מחשב, בעולמות מדומים, בסרטים ובסימולציות שונות.
הנה הפרקטלים שבטבע וכיצד ניתן ליצור אותם בעצמנו:
http://youtu.be/XwWyTts06tU
הבה נתקרב עוד ועוד לפרקטל הכי מוכר מקבוצת מנדלברוט:
http://youtu.be/gEw8xpb1aRA
הסבר על הפרקטלים של מנדלברוט:
http://youtu.be/STSS3_cVauk
ושיר על הסט של מנדלברוט:
http://youtu.be/ES-yKOYaXq0
האם ניסיתם פעם למדוד אורכו של משהו? - זה לא אמור להיות קשה, נכון?
אבל חופים הם לפעמים בעיה של ממש למודדים.. וזה לא רק לפעמים - חופים הם בעיקרון בעיה למודדים! - הם מדגימים היטב את הרעיון שהמימד הוא לא מוחלט אלא תלוי בסקלה שבה אנו מסתכלים או מודדים.
למה אנו מכוונים?
כשאנו מודדים את אורכו של קו חוף, נגלה תופעה מאד מוזרה - ככל נתקרב לקו החוף, יילך אורכו ויגדל. פרדוקס קו החוף הוא ההבחנה המדעית שאין לנו יכולת למדוד באמת את אורכו של קו חוף. כי ככל שהסרגל שלנו יהיה קטן יותר, ניאלץ נמדוד את החוף מקרוב יותר, הפיתולים שלו יימדדו ויאריכו את האורך הנמדד של קו החוף.
במילים אחרות - קו החוף יילך ויגדל, ככל שנמדוד אותו ביחידות קטנות יותר. למה זה קורה? - כי סרגל הוא ישר ולא ניתן להשתמש בו כדי למדוד פיתולים הקטנים יותר מאורכו. לפיכך, ככל שהסרגל הוא קטן יותר, נוכל למדוד אתו בתוך הפיתולים ואורכו הסופי של החוף יגדל משמעותית.
כמובן שפרדוקס קו החוף לא מדבר רק על חופים, אלא על כל דבר שאינו ישר. נוכל לראות תופעה דומה גם במדידה של אורך העיגול, של פני השטח של אלמוג, של מידות המוח וכדומה.
פרדוקס קו החוף הוא אחת הדוגמאות שהציג במחקריו המתמטיקאי בנואה מנדלברוט. הוא הדגים בעזרתו כיצד יכול השימוש בפרקטלים, אותם יצורים מתמטיים של דמיון עצמי, שמכילים את עצמם, לסייע בתיאור תופעות טבע, במקרה הזה את מבנה קו החוף. קראו עליהם באאוריקה בתגית "פרקטלים".
הנה סרטון הסבר לפרדוקס קו החוף:
https://youtu.be/kFjq8PX6F7I
והבעיה שמוצגת היטב במדידת אורכם של חופי אוסטרליה:
http://youtu.be/I_rw-AJqpCM
