שלום,
נראה שכבר הכרתם את אאוריקה. בטח כבר גיליתם כאן דברים מדהימים, אולי כבר שאלתם שאלות וקיבלתם תשובות טובות.
נשמח לראות משהו מכם בספר האורחים שלנו: איזו מילה טובה, חוות דעת, עצה חכמה לשיפור או כל מה שיש לכם לספר לנו על אאוריקה, כפי שאתם חווים אותה.
»
«
מהי סדרת פיבונאצ'י?
סדרת פיבונאצ'י במתמטיקה היא סדרת מספרים שהאיברים הראשונים בה הם 1 ו-1. כל איבר אחר בסדרת פיבונאצ'י שווה לסכום של שני האיברים הקודמים לו. 2 שווה ל-1 ועוד 1, 3 שווה 2+1, 5 הוא 2+3 וכן הלאה.
הסדרה קרויה על שם המתמטיקאי לאונרדו דה פיזה (לאונרדו מהעיר פיזה) שבאיטליה, שכונה "פיבונאצ'י". פיבונאצ'י תיאר את הסדרה הזו ב"ספר החשבוניה" שיצא בשנת 1202. הוא השתמש בסדרת פיבונאצ'י כדי לתאר את מספר הצאצאים של זוג ארנבים אחד. הוא תאר מצב שכל זוג ארנבים מגיל חודשיים ומעלה, ממליט מדי חודש זוג נוסף, התוצאות של מספר הצאצאים שלהם יהיו על פי הסדרה הזו.
מסתבר שהיחס בין שני איברים עוקבים של מספרי פיבונאצ'י שואף ל"יחס הזהב", קבוע מתמטי שתואר כבר ביוון העתיקה. תמיד כשמחלקים שני איברים עוקבים בסדרת פיבונאצ'י, התוצאה תלך ותתקרב לחתך הזהב. בדרך זו מוסברים דברים רבים בטבע בעזרת סדרת פיבונאצ'י והרקורסיה (ראו באאוריקה בתגית "מה זה, רקורסיה"), מקונכיות עם "ספירלת הזהב", דרך פרחים, כרובית, גלקסיות חלזוניות ועוד. וזה לא במקרה שסדרת פיבונאצ'י היא כה נפוצה בטבע - כמו שהראינו קודם בדוגמת הארנבים, מדובר בצורה היעילה ביותר לשכפול וכשצמחים ובעלי חיים פשוטים משכפלים תאים בגדילה - מקבלים בדיוק את הסדרה של פיבונאצ'י.
מקובל לסמן את איברי הסדרה באות F, שמוגדרת ברקורסיה - כלומר פעולה המבוצעת על ידי הפניה עצמית. במקרה הזה, כל F הוא סכום שני ה-Fים שלפניו.
הנה הסבר על סדרת פיבונאצ'י (עברית):
https://youtu.be/EAXKR-H_bS0
הסבר מדעי של הסדרה הפיבונאצ'ית (עברית):
http://youtu.be/z5RWfXTd3QU
הדגמה של סדרת פיבונאצ'י:
http://youtu.be/H2aHh5FLX5w
והסבר מתמטי של סדרת ה פיבונאצ'י (מתורגם):
https://youtu.be/SjSHVDfXHQ4
מה הפלא המתמטי של החמניה?
לאונרדו מפיזה, או פיבונאצ'י כמו שקרא לעצמו, היה כנראה גדול המתמטיקאים של ימי הביניים. במיוחד הוא ידוע כמי שגילה את סדרת המספרים המכונה על שמו "סדרת פיבונאצ'י".
כל איבר בסדרת פיבונאצ'י שווה לסכום של שני האיברים הקודמים לו. הוא לא הפסיק להתפעל מהקסם המתמטי של הסדרה הזו, כמו זה שביחסים בין ריבועי המספרים או ביופי של מה שהיא יוצרת בגאומטריה למשל, אבל אפילו הוא לא שיער כמה תופעות טבע מאופיינות במספרי פיבונאצ'י, כמו למשל העובדה שמספר עלי הכותרת בצמחים רבים הוא תמיד מספר פיבונצ'י, כמו 5, 8, 13 וכדומה.
מפתיע? - אז שימו לב לתופעה מרתקת אפילו יותר.. מסתבר שמספר הגרעינים שבפרח החמניה הם מספרי פיבונצ'י עוקבים. אם תביטו היטב, הם נראים כמו 2 ספירלות, שאחת היא בעלת 89 גרעינים והשנייה בת 55 גרעינים - שני מספרים עוקבים בסדרה (אגב, זה כך גם באצטרובלי עץ האורן).
ולמה זה קורה? - ובכן, נראה שהספירלות הללו מופיעות בפרחים כאלה ובאיצטרובלים, כדי למנוע מצב שבו הגרעינים יהיו צפופים מדי ויתקשו להתפתח. לכן הטבע מרבה אותם במספרי פיבונצ'י וכך נוצר המספר המרבי של גרעינים, מה שיבטיח שכפול מוצלח והמשך הדורות.
וזה לא הדבר היחיד שבו פיבונצ'י נראה בצמחים כאלו. מסתבר שאפילו זווית הגדילה של העלים על הגבעול, זו שמאפשרת לעלים החדשים לצמוח באופן שיקבלו הכי הרבה אור שמש, אפילו היא מתמטית ומדויקת. למעשה היא ידועה בתור יחס הזהב, כ-1.618. אם נחלק 360 מעלות של הגבעול העגול במספר 1.618 נקבל בדיוק את המיקומים שהטבע בחר לגדילת העלים על הגבעול. בינגו! - שוב הטבע הצטיין במתמטיקה והשתמש במספרי פיבונצ'י וביחס הזהב שנובע ממנו כדי להיטיב את גדילת הצמחים.
אז האמת שאין כאן פלא, חוץ מפלאי הטבע כמובן. סדרת פיבונאצ'י, שאנו כה מתפעלים ממנה כאן, היא הדרך שבה מאורגנים ומשוכפלים ביעילות מרכיבים רבים בטבע ובה פועלים ביעילות רבה כוחות טבעיים שונים. כשאנו מוצאים בחמניה את מספרי פיבונאצ'י, לכל היותר נוכל לומר שהחמניה "גדלה כמו שצריך".. אז אולי זה מופלא, אבל לא יותר מהפלא הבלתי נתפס של היקום כולו!
הנה המתמטיקה של החמניות:
https://youtu.be/z9d1mxgZ0ag
היופי המתמטי שגלום בסדרת מספרים פשוטה לכאורה זו (מתורגם):
https://youtu.be/SjSHVDfXHQ4
והגרעינים האלה שעל פרח החמנייה - ככה הם הופכים לגרעינים שחורים (עברית):
https://youtu.be/xLCkC0oOFqw
מי היה פיבונאצ'י ובאיזו סדרה הוא שיחק?
לאונרדו דה פיזה, מתמטיקאי מהעיר פיזה, כונה פשוט "פיבונאצ'י". פיבונאצ'י הוא זה שהביא לאירופה את הספרות ההודיות-ערביות, במקום הספרות הרומיות ששימשו את האירופאים עד אז. האמת היא שהעיסוק שלו בדברים שהסביבה לא הבינה, הוציא לו שם של ברנש מוזר. גם חתימתו בתור "הטייל" הוציאה לו שם של שוטה, שכן המילה משמשת גם לשוטים.
אך הוא עצמו עסק במתמטיקה מורכבת במיוחד. בהמשך חייו הוא אכן תרם למתמטיקה ולמדע את תרומתו האדירה, כשזיהה את "סדרת פיבונאצ'י", סדרת מספרים מופלאה שכל מספר הוא סכום הקודמים לו.
הצגת הסדרה וההגיון שבה פתחו פתח לזיהוי היחסים המדהימים שבין יופיים של הטבע והאמנות לבין הסדר המתמטי המדהים שבהם, סדר שהוגדר על ידי רבים כלא פחות מאשר "הפרופורציה האלוהית" (ראו באאוריקה בתגית "סדרת פיבונאצ'י"). בפשטות נאמר שזוהי סדרת מספרים שאם נחלק כל מספר בה במספר שקדם לו, נלך ונתקרב למספר 1.618. זהו המספר הידוע במתמטיקה, מאז היוונים הקדמונים, בתור "פיי" ("Phi"). אנו קוראים לו יחס הזהב והיוונים קשרו אותו אל היופי המושלם.
פיבונאצ'י הסביר שבמיני פרחים שונים ובאיצטרובלים - לאן שהביט הוא גילה בטבע את הצורות של הסדרה המתמטית שהציג. הוא גם זיהה את "מלבן הזהב" שנמצא בזרעי החמניות, בקונכיות, שבלולים, בצמחים סוקולנטיים, מיצירות אמנות ועד גלקסיות חלזוניות. חוקרים רבים אחריו גילו עד כמה נמצאים סדרת פיבונאצ'י ויחס הזהב בכל מקום.
כיום נחשב פיבונאצ'י בעיני רבים לגדול המתמטיקאים של ימי הביניים.
הנה סיפורו של פיבונאצי והסדרה המתמטית המופלאה שמצא (עברית):
https://youtu.be/EAXKR-H_bS0?t=8s
סרטון על לאונרדו פיבונצ'י:
http://youtu.be/wTlw7fNcO-0
הסבר לסדרת פיבונצ'י (מתורגם):
http://youtu.be/z5RWfXTd3QU
וסרט תיעודי על לאונרדו פיבונצ'י:
https://youtu.be/O2wU-HT7FiM?long=yes
איך נוצרים הגרעינים השחורים?
הם הפיצוחים הכי אהובים אצלנו. כשרואים משחק כדורגל או כדורסל בטלוויזיה הם כמעט מצרך חובה ויש אנשים רבים שאין אצלם סוף שבוע בלי לפצח גרעינים ובמיוחד את השחורים שבהם הוא לא סופ"ש. אולי סוף.
אז הגרעינים הלבנים הם גרעיני דלעת וגרעיני אבטיח באים מזרעי האבטיח, אבל מאיפה מגיעים הגרעינים השחורים?
הגרעינים השחורים הם גרעיני חמנית. קוטפים אותם בקיץ, בשעה מסוימת מאוד, בה הם נקטפים בקלות. בעבר קטפו אותם בידיים, אבל כיום קוצר אותם הקומביין הענק בשדה החמניות והם ייאגרו בו, עד שיועברו בשקים אל בית הקלייה.
בבית הקליה יקלו את כל סוגי הגרעינים - מהגרעינים השחורים, דרך גרעיני אבטיח וכמובן גרעינים לבנים, שבאים מהדלעת.
בבית הקליה, לאחר מכן, יארזו את הגרעינים האפויים בשקיות והם יישלחו לחנויות.
גרעיני החמנייה הם שהופכים לגרעינים שחורים (עברית):
https://youtu.be/xLCkC0oOFqw
גרעיני חמניה היו תמיד זולים וסיפקו בילוי נחמד והיו מי שהתפרנסו מהם היטב (עברית):
https://youtu.be/zRXRdRvz-3U
שיר שמדגים כמה הגרעינים מרכזיים בהוויה הישראלית (עברית):
https://youtu.be/WdWIFqhhwCs
והגרעינים הם חלק מהפיצוחים שאנו כה אוהבים (עברית):
https://youtu.be/zNfOKCcyK0g
מהי קונכיית הנאוטילוס העתיקה?
הנאוטילוס הוא מעין דיונון בעל קונכייה שיש לו כמה זרועות ציד קצרות. לקונכיית הנאוטילוס פסים בצבעי אדום ולבן. יש לו סיבה טובה להיות גאה בעצמו, שכן הוא מבעלי החיים היחידים ששרדו ללא שינוי מאז ימי הדינוזאורים ומהרכיכות היחידות ששרדו מתקופת המזוזואיקון. המבנה האורגני של הנאוטילוס לא השתנה במשך 400 מיליון שנה. לכן הנאוטילוס מוגדר כמאובן חי, מה שאומר שהיצורים הקרובים אליה נכחדו וקשה יותר למצוא יצורים כאלה שחיים, מאשר מאובנים של יצורים שנכחדו.
הנאוטילוס הוא קרוב משפחה של האמוניט הקדום, מתקופת המזוזואיקון. אבל בעוד שהאמוניט נכחד בהכחדה הגדולה שחיסלה גם את הדינוזאורים, לפני 65 מליון שנה, הצליח הנאוטילוס לשרוד את האירועים שהכחידו מינים רבים כל כך, מהאמוניטים ועד הדינוזאורים.
קונכיית הנאוטילוס היא דוגמה חלזונית שמדגימה את יחס הזהב בטבע (ראו בתגית "יחס הזהב") והיא בנויה על פי סדרת פיבונאצ'י.
הסופר הבדיוני הראשון והמפורסם ז'ול ורן קרא על שמה את הצוללת "נאוטילוס" מספרו "20,000 מיל מתחת לפני הים". בהמשך ההיסטוריה נשאו כמה צוללות אמיתיות את השם, כגון הצוללת שניסתה לחצות תחת הקוטב בשנת 1931 והצוללת הגרעינית הראשונה של הצבא האמריקאי.
הנה קונכיית הנאוטילוס:
http://youtu.be/HIRCI0G19Uw
המחקר עליה:
http://youtu.be/PIheRYcm6sI
נאוטילוס טורף:
https://youtu.be/vR6G-ANma1w
הנאוטילוס הוא אחת הדוגמאות הטבעיות הטובות של חתך הזהב:
https://youtu.be/_gxC8OjoQkQ
והתנועה האצילית של הנאוטילוס במים, כשבניגוד למנהגו הוא עולה ממעמקים אל פני הים:
https://youtu.be/dHqvQ8WBFeM
מה מיוחד במוזיאון גוגנהיים?
מוזיאון גוגנהיים בעיר ניו-יורק תוכנן על ידי האדריכל הידוע פרנק לויד רייט. רייט נדרש ל-700 שרטוטים ול-15 שנה עד שהצליח להגיע למה שרצה - מבנה שיהיה שונה מכל "הקופסאות" שמסביב.
ואכן, המבנה של מוזיאון גוגנהיים בניו-יורק הוא בעל צורה ייחודית שרבים מחשיבים כיצירת אמנות לא פחות חשובה מהיצירות המופשטות שמוצגות בו. הצורה המעוגלת, הלא סימטרית, הבלתי סדירה ושחלקה הרחב הוא דווקא למעלה היא בלתי נשכחת. הוא גם היה המוזיאון הראשון שבו הגלריה היא אחת - אין קומות ואין חדרים, אלא רק חלל אחד המתעקל בשיפוע מתון במורד המבנה, למלמעלה ועד לקומת הכניסה.
מה שאפשר את הקסם הזה, הוא התכנון של המבנה לפי סדרת פיבונאצ'י ועל פי יחס הזהב. ממש כמו קונכיית הנאוטילוס, הקונכייה הכי קדומה שעדיין קיימת בעולם ולא השתנתה מאז ימי הדינוזאורים.
את הרעיון קיבל האדריכל לאחר שהברונית העשירה מזמינת העבודה דרשה שהמבנה יהיה מעוגל. מכאן הדרך הייתה קצרה לחיקוי של קונכיית הנאוטילוס, שכולו מחושב על בסיס עיקרון פיבונאצ'י (ראו בתגית "סדרת פיבונאצ'י"). זהו עיקרון שמבוסס על חתך הזהב (ראו בתגית "יחס הזהב"), הצורה היעילה ביותר בטבע לשכפול מוקטן.
הנה סרטון של מוזיאון גוגנהיים:
https://youtu.be/QvgVKWvb2tI
שיטוט בחלל הפנימי של המוזיאון:
https://youtu.be/ypDTotRZPgY
הזמנה להגיע אליו:
https://youtu.be/OmAaZmACy20
והמבנה המיוחד של גוגנהיים והמודלים ששימשו בזמן התכנון:
https://youtu.be/O_YzxQecZMs
מה היופי של הברוקולי?
ברוקולי (Broccoli) הוא ירק עם ראשי פרחים ירוקים כהים, המסודרים בצורה שמזכירה עץ קטן. הוא קצת מזכיר קרובת משפחה שלו - הכרובית. למעשה, החלק שאנו אוכלים בברוקולי, הוא התפרחת הירוקה שלו. כן, הברוקולי הוא פרח אכיל.
אבל ברוקולי הוא גם אחת הדוגמאות היפות בטבע לפרקטלים, דברים שיש בהם דמיון עצמי. מהו דמיון עצמי? - אם תביטו היטב בברוקולי, תוכלו לראות שהוא מורכב מצורות של קונוסים (אצלנו בישראל נפוץ הזן העגול דווקא). מסתבר שאותם קונוסים בנויים על פי הגיון מתמטי מדהים שנקרא "סדרת פיבונאצ'י" (למדו על כך בהרחבה באאוריקה בתגית "סדרת פיבונאצ'י").
אבל הקונוסים שבברוקולי, חוזרים על עצמם בכל גודל בירק הזה. כל קונוס מורכב מחלקים שגם הם בצורת קונוס ובכל אחד מהם יש קונוסים קטנים וכך הלאה - הקונוסים של הברוקולי יחזרו שוב ושוב, בכל קנה מידה שנביט בו. זהו הפרקטל.
החוקרים משערים שמתי שהוא בתקופה הרומית החלו לפתח את הברוקולי, מצמח שנקרא כרוב בר. במשך מאות שנים השביחו אותו בתהליך של ברירה מלאכותית, על ידי דיכוי של התפתחות הפרחים. כך קיבל הגזע את מרב האנרגיה של הצמיחה.
רק במאה ה-16 החל הברוקולי לצאת מאיטליה למקומות אחרים באירופה, אבל הכניסה שלו למטבח האמיתי התרחשה במאה ה-20, כשהתגלו יתרונותיו התזונתיים וערכו הרפואי הרב.
מקור המלה "ברוקולי" הוא שיקוף של צורת העץ של הצמח הזה. הוא בא מהמלה הלטינית "ברקיום" שתהפוך באיטלקית ל"ברוקולו". פירושן הוא "ענף" או "זרוע".
הנה צמח וירק הברוקולי:
https://youtu.be/5AVu8XY5Zzw
הברוקולי מדגים היטב מהם פרקטלים:
https://youtu.be/XwWyTts06tU
כך הברוקולי גדל מהפרקטלים שלו:
https://youtu.be/CLiDcYuqT7w
גידול ואיסוף הברוקולי בשדות ארצות הברית:
https://youtu.be/kbTb3VRqZsY
וקלות העבודה אתו במטבח, כמו גם הערך התזונתי שלו, שהפכו את הברוקולי ללהיט (עברית):
https://youtu.be/6j3HpvcbimY
מה זה לוליין לוגריתמי?
לוליין לוגריתמי, ספירלה לוגריתמית, או ספירלת הזהב, הם שמות של אחת התופעות המרהיבות בטבע. מדובר בצורה גיאומטרית, של קו עקום ומעגלי המתחיל מנקודה כלשהי ומסתחרר בצורה מעגלית כלפי חוץ, כשהרדיוס של המעגל הולך וגדל, כמו חילזון (ספירלה).
צורה זו היא מעין צורה בסיסית של יופי. היא כוללת סימטריה והרמוניה - שתי התכונות שגורמות לבני אדם לזהות דבר יפה, כבר ממבט ראשון. כבר דורות מתואר הלוליין הלוגריתמי בתור "הפרופורציה האלוהית". כזו שיכולה להקנות לדברים שהאדם עושה את תכונות היופי הכי מוכרות, סימטריה והרמוניה.
שתי התוכנות הללו מתמזגות בלוליין הלוגריתמי. בזכותו הופכים הפרחים, למשל, ליפים בעינינו, כמו גם בעיני בעלי חיים. בזכות היופי ההרמוני והסימטריה המושלמת נמשכים אליהם הדבורים, הפרפרים והחרקים ומוצאים בהם מקור למזון וחיים.
השלמות והיופי הללו, של מה שקיבל את השם "יחס הזהב", גלומים בכל פינה בטבע. מפרחים כמו חמנית או ורד, פירות דוגמת אננס, ירקות כמו הכרוב והכרובית, צמחים כמו ברוקולי ואצל בעלי חיים כמו במראה קרני האיילים, פרפרים, שבלולים, קונכיות וחלזונות - כולם מתפתחים כך. גם בתופעות טבע כמו מערבולות מים ואוויר ואפילו גלקסיות עם מיליארדי כוכבים. כל אלה נראים כך. הסיבה היא שהאנרגיה הדרושה לכל אלה היא המינימלית. גדילה כזו של יצורים חיים, או קיומן של תופעות כמו מערבולת או אפילו גלקסיה, תובעות אנרגיה רבה. לכן חסכון טבעי בה הוא הכי טוב.
התופעות הללו משכו את תשומת לב האמנים ומתכנני המבנים, שכן יופיים לא משתנה והם נחשבים יפים בכל תקופה ובכל תרבות שהן. מקרני האיילים שהיו לקורות עמודים רומיים, אזור המפתחות בכלי המיתר ועד ללוליינים לוגריתמיים שהיו לכלי אמנותי בציור ובעיצוב והאדריכלות של מוזיאון גוגנהיים.
בצמחים ופרפרים רבים, גם כשהתכונות הללו לא נראות במבט ראשון, אפשר לדמיין את הצורה הלוליינית ומיד מזהים את ההרמוניה והסימטריה שהעין כה אוהבת.
הנה הספירלה של הלוליין הלוגריתמי שמופיעה בטבע בכל מקום:
https://youtu.be/nt2OlMAJj6o
ספירלת הזהב על פי פיבונאצ'י, היא הלוליין הלוגריתמי:
https://youtu.be/RKdrI9MZXHQ
תיאור של לוליין לוגריתמי בעזרת תוכנה מתמטית:
https://youtu.be/gXU1D2aF8QI
ומצגת וידאו של מרכיבים לולייניים שונים בטבע:
https://youtu.be/Qq7nU62ww0U
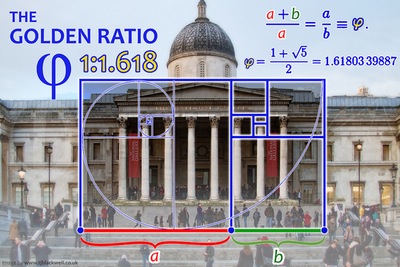
מהו יחס הזהב או חיתוך הזהב?
מדהים שחשבון יכול להיות קשור ליופי, לא?
אינכם מאמינים? - את יחס הזהב גילה ככל הנראה אחד מתלמידיו של הפילוסוף היווני פִּיתָגוֹרַס לפני כ-2,500 שנה. הוא שם לב שבני האדם הכי אוהבים צורה של מלבן שהיחס בין צלעותיו הוא יחס חשבוני של 1 ל-1.618. היחס הזה שיוצר "מלבן הזהב", יחס שמתקבל מחלוקת האורך שלו ברוחבו, התגלה כיפה בעיני אנשים בכל העולם. זהו "יחס הזהב" או "חיתוך הזהב", שמופיע במקומות רבים ובלתי-צפויים.
מאז הסתבר במחקרים שאם היו אנשים רבים ומגוונים מכל העולם והתקופות נשאלים איזה מרובע מבין מספר מרובעים שלפניהם הוא היפה והנעים ביותר לעין, רובם ככולם היו בוחרים במלבן הזהב. זה מראה שהיופי הוא אובייקטיבי, כלומר לא תלוי בתקופה, תרבות או אמונה.
ואכן, יחס הזהב, שיש שהמכנים גם "חתך הזהב", הוא יחס מתמטי שהמדע והאמנות עוסקים בו כבר מאות בשנים. תלמידי המתמטיקה מכירים אותו בתור המספר האי רציונלי שמסומן באות היוונית 'פִי' (φ). זהו מספר שמתחיל ב-1.6180339887 אבל הוא מכיל מספר אינסופי של ספרות אחרי הנקודה העשרונית.
יחס הזהב, שתואר לראשונה לפני כ-2,300 שנים בספר "יסודות" של אוקלידס, כונה אז "יחס קיצוני וממוצע". בתקופת הרנסאנס נכתבו מחקרים וספרים על "יחס הזהב" והוא קיבל את הכינוי "הפרופורציה האלוהית". בנו לפיו מבנים מפוארים, יצרו יצירות אמנות נשגבות, הלחינו מוסיקה ובמיוחד ראו אותו בטבע, כמעט בכל מקום.
התבוננות במלבן הזהב ממלאת בני האדם בתחושה של יופי ופרופורציה. כשמחלקים את אורכו של מלבן הזהב ברוחבו מקבלים את "יחס הזהב". היוונים הקדמונים והמצרים הקדמונים התייחסו אליו כשיא היופי האסתטי ותכננו לפיו מבנים מהיפים ביותר בעולם העתיק, כולל הפירמידות במצרים והפרתנון שבאקרופוליס של אתונה. באומנות מופיע יחס הזהב ברבים מהציורים שבהם יש יחס פרופורציוני בין גדלים שונים.
כאמור, בנוסף לאמנות, אדריכלות ותחומי אסתטיקה אחרים שמשתמשים לא מעט ביחס הזהב, גם בטבע ניתן לראותו, במבנים של קונכיות ושבלולים, בסידור העלים מסביב לגבעולים, במערבולות, סופות טורנדו ועד לגלקסיות חלזוניות.
יש גם טענה שיחס הזהב הוא שמסביר את העובדה שאנו שכולנו מזהים את אותן פנים יפות ומבנה גוף יפה. כאן כמובן שיש מחלוקות, כי הוכח לא פעם שגם אם פנים שבנויות על פי יחס הזהב הן יפות, הרבה פנים שנחשבים יפים בקרב הציבור, כמו מרילין מונרו למשל, לא מחולקים על פי יחס הזהב.. האם הם מכוערים?
הנה סרטון הסבר על יחס הזהב (עברית):
https://youtu.be/co2k2bcZ1h0
יחס הזהב והקשר בינו לבין מה שאנו רואים כיופי (מתורגם):
http://youtu.be/_cIlomNxxig
יחס הזהב דרך סדרת פיבונאצ'י, בה יש בין כל שני מספרים יחס הנוטה ליחס הזהב (מתורגם):
http://youtu.be/z5RWfXTd3QU
איך יחס הזהב בונה את המלבנים שהקשתות שעוברות בהם יוצרות את סדרת פיבונאצ'י:
http://youtu.be/kkGeOWYOFoA
ההקשרים השונים של פי ויחס הזהב:
http://youtu.be/0hvD5kLqjuw
וסרט תיעודי על יחס הזהב:
https://youtu.be/gLml9nltl6M?long=yes
סדרת פיבונאצ'י במתמטיקה היא סדרת מספרים שהאיברים הראשונים בה הם 1 ו-1. כל איבר אחר בסדרת פיבונאצ'י שווה לסכום של שני האיברים הקודמים לו. 2 שווה ל-1 ועוד 1, 3 שווה 2+1, 5 הוא 2+3 וכן הלאה.
הסדרה קרויה על שם המתמטיקאי לאונרדו דה פיזה (לאונרדו מהעיר פיזה) שבאיטליה, שכונה "פיבונאצ'י". פיבונאצ'י תיאר את הסדרה הזו ב"ספר החשבוניה" שיצא בשנת 1202. הוא השתמש בסדרת פיבונאצ'י כדי לתאר את מספר הצאצאים של זוג ארנבים אחד. הוא תאר מצב שכל זוג ארנבים מגיל חודשיים ומעלה, ממליט מדי חודש זוג נוסף, התוצאות של מספר הצאצאים שלהם יהיו על פי הסדרה הזו.
מסתבר שהיחס בין שני איברים עוקבים של מספרי פיבונאצ'י שואף ל"יחס הזהב", קבוע מתמטי שתואר כבר ביוון העתיקה. תמיד כשמחלקים שני איברים עוקבים בסדרת פיבונאצ'י, התוצאה תלך ותתקרב לחתך הזהב. בדרך זו מוסברים דברים רבים בטבע בעזרת סדרת פיבונאצ'י והרקורסיה (ראו באאוריקה בתגית "מה זה, רקורסיה"), מקונכיות עם "ספירלת הזהב", דרך פרחים, כרובית, גלקסיות חלזוניות ועוד. וזה לא במקרה שסדרת פיבונאצ'י היא כה נפוצה בטבע - כמו שהראינו קודם בדוגמת הארנבים, מדובר בצורה היעילה ביותר לשכפול וכשצמחים ובעלי חיים פשוטים משכפלים תאים בגדילה - מקבלים בדיוק את הסדרה של פיבונאצ'י.
מקובל לסמן את איברי הסדרה באות F, שמוגדרת ברקורסיה - כלומר פעולה המבוצעת על ידי הפניה עצמית. במקרה הזה, כל F הוא סכום שני ה-Fים שלפניו.
הנה הסבר על סדרת פיבונאצ'י (עברית):
https://youtu.be/EAXKR-H_bS0
הסבר מדעי של הסדרה הפיבונאצ'ית (עברית):
http://youtu.be/z5RWfXTd3QU
הדגמה של סדרת פיבונאצ'י:
http://youtu.be/H2aHh5FLX5w
והסבר מתמטי של סדרת ה פיבונאצ'י (מתורגם):
https://youtu.be/SjSHVDfXHQ4
לאונרדו מפיזה, או פיבונאצ'י כמו שקרא לעצמו, היה כנראה גדול המתמטיקאים של ימי הביניים. במיוחד הוא ידוע כמי שגילה את סדרת המספרים המכונה על שמו "סדרת פיבונאצ'י".
כל איבר בסדרת פיבונאצ'י שווה לסכום של שני האיברים הקודמים לו. הוא לא הפסיק להתפעל מהקסם המתמטי של הסדרה הזו, כמו זה שביחסים בין ריבועי המספרים או ביופי של מה שהיא יוצרת בגאומטריה למשל, אבל אפילו הוא לא שיער כמה תופעות טבע מאופיינות במספרי פיבונאצ'י, כמו למשל העובדה שמספר עלי הכותרת בצמחים רבים הוא תמיד מספר פיבונצ'י, כמו 5, 8, 13 וכדומה.
מפתיע? - אז שימו לב לתופעה מרתקת אפילו יותר.. מסתבר שמספר הגרעינים שבפרח החמניה הם מספרי פיבונצ'י עוקבים. אם תביטו היטב, הם נראים כמו 2 ספירלות, שאחת היא בעלת 89 גרעינים והשנייה בת 55 גרעינים - שני מספרים עוקבים בסדרה (אגב, זה כך גם באצטרובלי עץ האורן).
ולמה זה קורה? - ובכן, נראה שהספירלות הללו מופיעות בפרחים כאלה ובאיצטרובלים, כדי למנוע מצב שבו הגרעינים יהיו צפופים מדי ויתקשו להתפתח. לכן הטבע מרבה אותם במספרי פיבונצ'י וכך נוצר המספר המרבי של גרעינים, מה שיבטיח שכפול מוצלח והמשך הדורות.
וזה לא הדבר היחיד שבו פיבונצ'י נראה בצמחים כאלו. מסתבר שאפילו זווית הגדילה של העלים על הגבעול, זו שמאפשרת לעלים החדשים לצמוח באופן שיקבלו הכי הרבה אור שמש, אפילו היא מתמטית ומדויקת. למעשה היא ידועה בתור יחס הזהב, כ-1.618. אם נחלק 360 מעלות של הגבעול העגול במספר 1.618 נקבל בדיוק את המיקומים שהטבע בחר לגדילת העלים על הגבעול. בינגו! - שוב הטבע הצטיין במתמטיקה והשתמש במספרי פיבונצ'י וביחס הזהב שנובע ממנו כדי להיטיב את גדילת הצמחים.
אז האמת שאין כאן פלא, חוץ מפלאי הטבע כמובן. סדרת פיבונאצ'י, שאנו כה מתפעלים ממנה כאן, היא הדרך שבה מאורגנים ומשוכפלים ביעילות מרכיבים רבים בטבע ובה פועלים ביעילות רבה כוחות טבעיים שונים. כשאנו מוצאים בחמניה את מספרי פיבונאצ'י, לכל היותר נוכל לומר שהחמניה "גדלה כמו שצריך".. אז אולי זה מופלא, אבל לא יותר מהפלא הבלתי נתפס של היקום כולו!
הנה המתמטיקה של החמניות:
https://youtu.be/z9d1mxgZ0ag
היופי המתמטי שגלום בסדרת מספרים פשוטה לכאורה זו (מתורגם):
https://youtu.be/SjSHVDfXHQ4
והגרעינים האלה שעל פרח החמנייה - ככה הם הופכים לגרעינים שחורים (עברית):
https://youtu.be/xLCkC0oOFqw
לאונרדו דה פיזה, מתמטיקאי מהעיר פיזה, כונה פשוט "פיבונאצ'י". פיבונאצ'י הוא זה שהביא לאירופה את הספרות ההודיות-ערביות, במקום הספרות הרומיות ששימשו את האירופאים עד אז. האמת היא שהעיסוק שלו בדברים שהסביבה לא הבינה, הוציא לו שם של ברנש מוזר. גם חתימתו בתור "הטייל" הוציאה לו שם של שוטה, שכן המילה משמשת גם לשוטים.
אך הוא עצמו עסק במתמטיקה מורכבת במיוחד. בהמשך חייו הוא אכן תרם למתמטיקה ולמדע את תרומתו האדירה, כשזיהה את "סדרת פיבונאצ'י", סדרת מספרים מופלאה שכל מספר הוא סכום הקודמים לו.
הצגת הסדרה וההגיון שבה פתחו פתח לזיהוי היחסים המדהימים שבין יופיים של הטבע והאמנות לבין הסדר המתמטי המדהים שבהם, סדר שהוגדר על ידי רבים כלא פחות מאשר "הפרופורציה האלוהית" (ראו באאוריקה בתגית "סדרת פיבונאצ'י"). בפשטות נאמר שזוהי סדרת מספרים שאם נחלק כל מספר בה במספר שקדם לו, נלך ונתקרב למספר 1.618. זהו המספר הידוע במתמטיקה, מאז היוונים הקדמונים, בתור "פיי" ("Phi"). אנו קוראים לו יחס הזהב והיוונים קשרו אותו אל היופי המושלם.
פיבונאצ'י הסביר שבמיני פרחים שונים ובאיצטרובלים - לאן שהביט הוא גילה בטבע את הצורות של הסדרה המתמטית שהציג. הוא גם זיהה את "מלבן הזהב" שנמצא בזרעי החמניות, בקונכיות, שבלולים, בצמחים סוקולנטיים, מיצירות אמנות ועד גלקסיות חלזוניות. חוקרים רבים אחריו גילו עד כמה נמצאים סדרת פיבונאצ'י ויחס הזהב בכל מקום.
כיום נחשב פיבונאצ'י בעיני רבים לגדול המתמטיקאים של ימי הביניים.
הנה סיפורו של פיבונאצי והסדרה המתמטית המופלאה שמצא (עברית):
https://youtu.be/EAXKR-H_bS0?t=8s
סרטון על לאונרדו פיבונצ'י:
http://youtu.be/wTlw7fNcO-0
הסבר לסדרת פיבונצ'י (מתורגם):
http://youtu.be/z5RWfXTd3QU
וסרט תיעודי על לאונרדו פיבונצ'י:
https://youtu.be/O2wU-HT7FiM?long=yes
הם הפיצוחים הכי אהובים אצלנו. כשרואים משחק כדורגל או כדורסל בטלוויזיה הם כמעט מצרך חובה ויש אנשים רבים שאין אצלם סוף שבוע בלי לפצח גרעינים ובמיוחד את השחורים שבהם הוא לא סופ"ש. אולי סוף.
אז הגרעינים הלבנים הם גרעיני דלעת וגרעיני אבטיח באים מזרעי האבטיח, אבל מאיפה מגיעים הגרעינים השחורים?
הגרעינים השחורים הם גרעיני חמנית. קוטפים אותם בקיץ, בשעה מסוימת מאוד, בה הם נקטפים בקלות. בעבר קטפו אותם בידיים, אבל כיום קוצר אותם הקומביין הענק בשדה החמניות והם ייאגרו בו, עד שיועברו בשקים אל בית הקלייה.
בבית הקליה יקלו את כל סוגי הגרעינים - מהגרעינים השחורים, דרך גרעיני אבטיח וכמובן גרעינים לבנים, שבאים מהדלעת.
בבית הקליה, לאחר מכן, יארזו את הגרעינים האפויים בשקיות והם יישלחו לחנויות.
גרעיני החמנייה הם שהופכים לגרעינים שחורים (עברית):
https://youtu.be/xLCkC0oOFqw
גרעיני חמניה היו תמיד זולים וסיפקו בילוי נחמד והיו מי שהתפרנסו מהם היטב (עברית):
https://youtu.be/zRXRdRvz-3U
שיר שמדגים כמה הגרעינים מרכזיים בהוויה הישראלית (עברית):
https://youtu.be/WdWIFqhhwCs
והגרעינים הם חלק מהפיצוחים שאנו כה אוהבים (עברית):
https://youtu.be/zNfOKCcyK0g
סדרת פיבונאצ'י
הנאוטילוס הוא מעין דיונון בעל קונכייה שיש לו כמה זרועות ציד קצרות. לקונכיית הנאוטילוס פסים בצבעי אדום ולבן. יש לו סיבה טובה להיות גאה בעצמו, שכן הוא מבעלי החיים היחידים ששרדו ללא שינוי מאז ימי הדינוזאורים ומהרכיכות היחידות ששרדו מתקופת המזוזואיקון. המבנה האורגני של הנאוטילוס לא השתנה במשך 400 מיליון שנה. לכן הנאוטילוס מוגדר כמאובן חי, מה שאומר שהיצורים הקרובים אליה נכחדו וקשה יותר למצוא יצורים כאלה שחיים, מאשר מאובנים של יצורים שנכחדו.
הנאוטילוס הוא קרוב משפחה של האמוניט הקדום, מתקופת המזוזואיקון. אבל בעוד שהאמוניט נכחד בהכחדה הגדולה שחיסלה גם את הדינוזאורים, לפני 65 מליון שנה, הצליח הנאוטילוס לשרוד את האירועים שהכחידו מינים רבים כל כך, מהאמוניטים ועד הדינוזאורים.
קונכיית הנאוטילוס היא דוגמה חלזונית שמדגימה את יחס הזהב בטבע (ראו בתגית "יחס הזהב") והיא בנויה על פי סדרת פיבונאצ'י.
הסופר הבדיוני הראשון והמפורסם ז'ול ורן קרא על שמה את הצוללת "נאוטילוס" מספרו "20,000 מיל מתחת לפני הים". בהמשך ההיסטוריה נשאו כמה צוללות אמיתיות את השם, כגון הצוללת שניסתה לחצות תחת הקוטב בשנת 1931 והצוללת הגרעינית הראשונה של הצבא האמריקאי.
הנה קונכיית הנאוטילוס:
http://youtu.be/HIRCI0G19Uw
המחקר עליה:
http://youtu.be/PIheRYcm6sI
נאוטילוס טורף:
https://youtu.be/vR6G-ANma1w
הנאוטילוס הוא אחת הדוגמאות הטבעיות הטובות של חתך הזהב:
https://youtu.be/_gxC8OjoQkQ
והתנועה האצילית של הנאוטילוס במים, כשבניגוד למנהגו הוא עולה ממעמקים אל פני הים:
https://youtu.be/dHqvQ8WBFeM
מוזיאון גוגנהיים בעיר ניו-יורק תוכנן על ידי האדריכל הידוע פרנק לויד רייט. רייט נדרש ל-700 שרטוטים ול-15 שנה עד שהצליח להגיע למה שרצה - מבנה שיהיה שונה מכל "הקופסאות" שמסביב.
ואכן, המבנה של מוזיאון גוגנהיים בניו-יורק הוא בעל צורה ייחודית שרבים מחשיבים כיצירת אמנות לא פחות חשובה מהיצירות המופשטות שמוצגות בו. הצורה המעוגלת, הלא סימטרית, הבלתי סדירה ושחלקה הרחב הוא דווקא למעלה היא בלתי נשכחת. הוא גם היה המוזיאון הראשון שבו הגלריה היא אחת - אין קומות ואין חדרים, אלא רק חלל אחד המתעקל בשיפוע מתון במורד המבנה, למלמעלה ועד לקומת הכניסה.
מה שאפשר את הקסם הזה, הוא התכנון של המבנה לפי סדרת פיבונאצ'י ועל פי יחס הזהב. ממש כמו קונכיית הנאוטילוס, הקונכייה הכי קדומה שעדיין קיימת בעולם ולא השתנתה מאז ימי הדינוזאורים.
את הרעיון קיבל האדריכל לאחר שהברונית העשירה מזמינת העבודה דרשה שהמבנה יהיה מעוגל. מכאן הדרך הייתה קצרה לחיקוי של קונכיית הנאוטילוס, שכולו מחושב על בסיס עיקרון פיבונאצ'י (ראו בתגית "סדרת פיבונאצ'י"). זהו עיקרון שמבוסס על חתך הזהב (ראו בתגית "יחס הזהב"), הצורה היעילה ביותר בטבע לשכפול מוקטן.
הנה סרטון של מוזיאון גוגנהיים:
https://youtu.be/QvgVKWvb2tI
שיטוט בחלל הפנימי של המוזיאון:
https://youtu.be/ypDTotRZPgY
הזמנה להגיע אליו:
https://youtu.be/OmAaZmACy20
והמבנה המיוחד של גוגנהיים והמודלים ששימשו בזמן התכנון:
https://youtu.be/O_YzxQecZMs
ברוקולי (Broccoli) הוא ירק עם ראשי פרחים ירוקים כהים, המסודרים בצורה שמזכירה עץ קטן. הוא קצת מזכיר קרובת משפחה שלו - הכרובית. למעשה, החלק שאנו אוכלים בברוקולי, הוא התפרחת הירוקה שלו. כן, הברוקולי הוא פרח אכיל.
אבל ברוקולי הוא גם אחת הדוגמאות היפות בטבע לפרקטלים, דברים שיש בהם דמיון עצמי. מהו דמיון עצמי? - אם תביטו היטב בברוקולי, תוכלו לראות שהוא מורכב מצורות של קונוסים (אצלנו בישראל נפוץ הזן העגול דווקא). מסתבר שאותם קונוסים בנויים על פי הגיון מתמטי מדהים שנקרא "סדרת פיבונאצ'י" (למדו על כך בהרחבה באאוריקה בתגית "סדרת פיבונאצ'י").
אבל הקונוסים שבברוקולי, חוזרים על עצמם בכל גודל בירק הזה. כל קונוס מורכב מחלקים שגם הם בצורת קונוס ובכל אחד מהם יש קונוסים קטנים וכך הלאה - הקונוסים של הברוקולי יחזרו שוב ושוב, בכל קנה מידה שנביט בו. זהו הפרקטל.
החוקרים משערים שמתי שהוא בתקופה הרומית החלו לפתח את הברוקולי, מצמח שנקרא כרוב בר. במשך מאות שנים השביחו אותו בתהליך של ברירה מלאכותית, על ידי דיכוי של התפתחות הפרחים. כך קיבל הגזע את מרב האנרגיה של הצמיחה.
רק במאה ה-16 החל הברוקולי לצאת מאיטליה למקומות אחרים באירופה, אבל הכניסה שלו למטבח האמיתי התרחשה במאה ה-20, כשהתגלו יתרונותיו התזונתיים וערכו הרפואי הרב.
מקור המלה "ברוקולי" הוא שיקוף של צורת העץ של הצמח הזה. הוא בא מהמלה הלטינית "ברקיום" שתהפוך באיטלקית ל"ברוקולו". פירושן הוא "ענף" או "זרוע".
הנה צמח וירק הברוקולי:
https://youtu.be/5AVu8XY5Zzw
הברוקולי מדגים היטב מהם פרקטלים:
https://youtu.be/XwWyTts06tU
כך הברוקולי גדל מהפרקטלים שלו:
https://youtu.be/CLiDcYuqT7w
גידול ואיסוף הברוקולי בשדות ארצות הברית:
https://youtu.be/kbTb3VRqZsY
וקלות העבודה אתו במטבח, כמו גם הערך התזונתי שלו, שהפכו את הברוקולי ללהיט (עברית):
https://youtu.be/6j3HpvcbimY
לוליין לוגריתמי, ספירלה לוגריתמית, או ספירלת הזהב, הם שמות של אחת התופעות המרהיבות בטבע. מדובר בצורה גיאומטרית, של קו עקום ומעגלי המתחיל מנקודה כלשהי ומסתחרר בצורה מעגלית כלפי חוץ, כשהרדיוס של המעגל הולך וגדל, כמו חילזון (ספירלה).
צורה זו היא מעין צורה בסיסית של יופי. היא כוללת סימטריה והרמוניה - שתי התכונות שגורמות לבני אדם לזהות דבר יפה, כבר ממבט ראשון. כבר דורות מתואר הלוליין הלוגריתמי בתור "הפרופורציה האלוהית". כזו שיכולה להקנות לדברים שהאדם עושה את תכונות היופי הכי מוכרות, סימטריה והרמוניה.
שתי התוכנות הללו מתמזגות בלוליין הלוגריתמי. בזכותו הופכים הפרחים, למשל, ליפים בעינינו, כמו גם בעיני בעלי חיים. בזכות היופי ההרמוני והסימטריה המושלמת נמשכים אליהם הדבורים, הפרפרים והחרקים ומוצאים בהם מקור למזון וחיים.
השלמות והיופי הללו, של מה שקיבל את השם "יחס הזהב", גלומים בכל פינה בטבע. מפרחים כמו חמנית או ורד, פירות דוגמת אננס, ירקות כמו הכרוב והכרובית, צמחים כמו ברוקולי ואצל בעלי חיים כמו במראה קרני האיילים, פרפרים, שבלולים, קונכיות וחלזונות - כולם מתפתחים כך. גם בתופעות טבע כמו מערבולות מים ואוויר ואפילו גלקסיות עם מיליארדי כוכבים. כל אלה נראים כך. הסיבה היא שהאנרגיה הדרושה לכל אלה היא המינימלית. גדילה כזו של יצורים חיים, או קיומן של תופעות כמו מערבולת או אפילו גלקסיה, תובעות אנרגיה רבה. לכן חסכון טבעי בה הוא הכי טוב.
התופעות הללו משכו את תשומת לב האמנים ומתכנני המבנים, שכן יופיים לא משתנה והם נחשבים יפים בכל תקופה ובכל תרבות שהן. מקרני האיילים שהיו לקורות עמודים רומיים, אזור המפתחות בכלי המיתר ועד ללוליינים לוגריתמיים שהיו לכלי אמנותי בציור ובעיצוב והאדריכלות של מוזיאון גוגנהיים.
בצמחים ופרפרים רבים, גם כשהתכונות הללו לא נראות במבט ראשון, אפשר לדמיין את הצורה הלוליינית ומיד מזהים את ההרמוניה והסימטריה שהעין כה אוהבת.
הנה הספירלה של הלוליין הלוגריתמי שמופיעה בטבע בכל מקום:
https://youtu.be/nt2OlMAJj6o
ספירלת הזהב על פי פיבונאצ'י, היא הלוליין הלוגריתמי:
https://youtu.be/RKdrI9MZXHQ
תיאור של לוליין לוגריתמי בעזרת תוכנה מתמטית:
https://youtu.be/gXU1D2aF8QI
ומצגת וידאו של מרכיבים לולייניים שונים בטבע:
https://youtu.be/Qq7nU62ww0U
מדהים שחשבון יכול להיות קשור ליופי, לא?
אינכם מאמינים? - את יחס הזהב גילה ככל הנראה אחד מתלמידיו של הפילוסוף היווני פִּיתָגוֹרַס לפני כ-2,500 שנה. הוא שם לב שבני האדם הכי אוהבים צורה של מלבן שהיחס בין צלעותיו הוא יחס חשבוני של 1 ל-1.618. היחס הזה שיוצר "מלבן הזהב", יחס שמתקבל מחלוקת האורך שלו ברוחבו, התגלה כיפה בעיני אנשים בכל העולם. זהו "יחס הזהב" או "חיתוך הזהב", שמופיע במקומות רבים ובלתי-צפויים.
מאז הסתבר במחקרים שאם היו אנשים רבים ומגוונים מכל העולם והתקופות נשאלים איזה מרובע מבין מספר מרובעים שלפניהם הוא היפה והנעים ביותר לעין, רובם ככולם היו בוחרים במלבן הזהב. זה מראה שהיופי הוא אובייקטיבי, כלומר לא תלוי בתקופה, תרבות או אמונה.
ואכן, יחס הזהב, שיש שהמכנים גם "חתך הזהב", הוא יחס מתמטי שהמדע והאמנות עוסקים בו כבר מאות בשנים. תלמידי המתמטיקה מכירים אותו בתור המספר האי רציונלי שמסומן באות היוונית 'פִי' (φ). זהו מספר שמתחיל ב-1.6180339887 אבל הוא מכיל מספר אינסופי של ספרות אחרי הנקודה העשרונית.
יחס הזהב, שתואר לראשונה לפני כ-2,300 שנים בספר "יסודות" של אוקלידס, כונה אז "יחס קיצוני וממוצע". בתקופת הרנסאנס נכתבו מחקרים וספרים על "יחס הזהב" והוא קיבל את הכינוי "הפרופורציה האלוהית". בנו לפיו מבנים מפוארים, יצרו יצירות אמנות נשגבות, הלחינו מוסיקה ובמיוחד ראו אותו בטבע, כמעט בכל מקום.
התבוננות במלבן הזהב ממלאת בני האדם בתחושה של יופי ופרופורציה. כשמחלקים את אורכו של מלבן הזהב ברוחבו מקבלים את "יחס הזהב". היוונים הקדמונים והמצרים הקדמונים התייחסו אליו כשיא היופי האסתטי ותכננו לפיו מבנים מהיפים ביותר בעולם העתיק, כולל הפירמידות במצרים והפרתנון שבאקרופוליס של אתונה. באומנות מופיע יחס הזהב ברבים מהציורים שבהם יש יחס פרופורציוני בין גדלים שונים.
כאמור, בנוסף לאמנות, אדריכלות ותחומי אסתטיקה אחרים שמשתמשים לא מעט ביחס הזהב, גם בטבע ניתן לראותו, במבנים של קונכיות ושבלולים, בסידור העלים מסביב לגבעולים, במערבולות, סופות טורנדו ועד לגלקסיות חלזוניות.
יש גם טענה שיחס הזהב הוא שמסביר את העובדה שאנו שכולנו מזהים את אותן פנים יפות ומבנה גוף יפה. כאן כמובן שיש מחלוקות, כי הוכח לא פעם שגם אם פנים שבנויות על פי יחס הזהב הן יפות, הרבה פנים שנחשבים יפים בקרב הציבור, כמו מרילין מונרו למשל, לא מחולקים על פי יחס הזהב.. האם הם מכוערים?
הנה סרטון הסבר על יחס הזהב (עברית):
https://youtu.be/co2k2bcZ1h0
יחס הזהב והקשר בינו לבין מה שאנו רואים כיופי (מתורגם):
http://youtu.be/_cIlomNxxig
יחס הזהב דרך סדרת פיבונאצ'י, בה יש בין כל שני מספרים יחס הנוטה ליחס הזהב (מתורגם):
http://youtu.be/z5RWfXTd3QU
איך יחס הזהב בונה את המלבנים שהקשתות שעוברות בהם יוצרות את סדרת פיבונאצ'י:
http://youtu.be/kkGeOWYOFoA
ההקשרים השונים של פי ויחס הזהב:
http://youtu.be/0hvD5kLqjuw
וסרט תיעודי על יחס הזהב:
https://youtu.be/gLml9nltl6M?long=yes
מהי הפרופורציה האלוהית?
זה קרה בשנת 1202 כשמתמטיקאי קדום ורב זכויות סיפר את סיפור הארנבים, שמולידים צאצא אחד בכל חודש ומתרבים בקצב לוגריתמי. הוא הציג לעולם סדרת מספרים שסכום כל שני מספרים עוקבים בה יהיה המספר הבא. אבל הסדרה הזו צפנה סודות נוספים ומדהימים. תוכלו ללמוד עליהם לעומק באאוריקה, בתגית "סדרת פיבונאצ'י".
אבל המעניין הוא שכמעט מבלי משים חשף פיבונאצ'י בתגלית שלו את אחד מסודות האסתטיקה המעניינים בהיסטוריה. הוא גילה שיופי ומתמטיקה הלכו במשך אלפי שנים יד ביד, כשאמנים, אדריכלים ויוצרים מכל הזמנים אחזו בתפיסת יופי ואסתטיקה דומים, מבלי לתאם זאת ביניהם.
ועוד יותר, הוא זיהה שהתפיסה הזו טבעית ומשותפת לכל בני האדם, בלי הבדל של תרבות, מקום וזמן. בכל כיוון שאליו נפנה מבט, נוכל לראות את אצבע אלוהים, או לפחות את מודל היופי שהוא יצר בטבע ושבאופן בלתי תלוי אימצו כל התרבויות העתיקות. מקונכיות וחלזונות, דרך פרחים ואיצטרובלים ועד לגלקסיות שלמות - הטבע מוצף ביחס הזהב שגילה פיבונאצ'י.
מסתבר שהמתמטיקה גילתה את הדרך היעילה ביותר לשכפול של תאים ולתנועה בחלל וזו, אם תרצו, יצרה פרופורציה שכולה אצבע אלוהים.
הנה הפרופורציה האלוהית שהלכה והתגלתה מאז פיבונאצ'י:
http://youtu.be/03uC9bhX0Rc
הדוגמאות הרבות של הפרופורציה האלוהית בעולם:
http://youtu.be/0hvD5kLqjuw
קבלו נסיון לבחון את המונה ליזה וכיצד יצר לאונרדו, כמו אמנים רבים, תמונה עם פרופורציות מושלמות שלמד מהטבע:
http://youtu.be/JFTSAjZEqPw
הסבר של הפרופורציה האלוהית וטענה די מוזרה שמסתירים אותה מהציבור:
http://youtu.be/4VrcO6JaMrM
וסרטון תיעודי על המתמטיקה המופלאה של פיבונאצ'י שמייצרת את היופי הזה:
https://youtu.be/keLN89CWZ-A?long=yes
זה קרה בשנת 1202 כשמתמטיקאי קדום ורב זכויות סיפר את סיפור הארנבים, שמולידים צאצא אחד בכל חודש ומתרבים בקצב לוגריתמי. הוא הציג לעולם סדרת מספרים שסכום כל שני מספרים עוקבים בה יהיה המספר הבא. אבל הסדרה הזו צפנה סודות נוספים ומדהימים. תוכלו ללמוד עליהם לעומק באאוריקה, בתגית "סדרת פיבונאצ'י".
אבל המעניין הוא שכמעט מבלי משים חשף פיבונאצ'י בתגלית שלו את אחד מסודות האסתטיקה המעניינים בהיסטוריה. הוא גילה שיופי ומתמטיקה הלכו במשך אלפי שנים יד ביד, כשאמנים, אדריכלים ויוצרים מכל הזמנים אחזו בתפיסת יופי ואסתטיקה דומים, מבלי לתאם זאת ביניהם.
ועוד יותר, הוא זיהה שהתפיסה הזו טבעית ומשותפת לכל בני האדם, בלי הבדל של תרבות, מקום וזמן. בכל כיוון שאליו נפנה מבט, נוכל לראות את אצבע אלוהים, או לפחות את מודל היופי שהוא יצר בטבע ושבאופן בלתי תלוי אימצו כל התרבויות העתיקות. מקונכיות וחלזונות, דרך פרחים ואיצטרובלים ועד לגלקסיות שלמות - הטבע מוצף ביחס הזהב שגילה פיבונאצ'י.
מסתבר שהמתמטיקה גילתה את הדרך היעילה ביותר לשכפול של תאים ולתנועה בחלל וזו, אם תרצו, יצרה פרופורציה שכולה אצבע אלוהים.
הנה הפרופורציה האלוהית שהלכה והתגלתה מאז פיבונאצ'י:
http://youtu.be/03uC9bhX0Rc
הדוגמאות הרבות של הפרופורציה האלוהית בעולם:
http://youtu.be/0hvD5kLqjuw
קבלו נסיון לבחון את המונה ליזה וכיצד יצר לאונרדו, כמו אמנים רבים, תמונה עם פרופורציות מושלמות שלמד מהטבע:
http://youtu.be/JFTSAjZEqPw
הסבר של הפרופורציה האלוהית וטענה די מוזרה שמסתירים אותה מהציבור:
http://youtu.be/4VrcO6JaMrM
וסרטון תיעודי על המתמטיקה המופלאה של פיבונאצ'י שמייצרת את היופי הזה:
https://youtu.be/keLN89CWZ-A?long=yes
מהו מלבן הזהב?
מסתבר שאם היו אנשים רבים ומגוונים מכל העולם והתקופות נשאלים איזה מרובע מבין מספר מרובעים שלפניהם הוא היפה והנעים ביותר לעין, היו בוחרים רובם ככולם במלבן הזהב. מלבן הזהב הוא מלבן שהיחס בין אורכו לרוחבו הוא יחס שזכה גם הוא לכינוי יחס הזהב. כשהאורך של מלבן גדול פי בערך 1.618 מהרוחב שלו, מתקיים יחס מושלם ביניהם והוא נקרא מלבן הזהב. מלבן הזהב מוכיח שהיופי הוא אובייקטיבי, כלומר לא תלוי בתקופה, תרבות או אמונה.
כיוון שיחס הזהב הוא כה יפה ומושלם בעיני המתבוננים, הוא זכה לכינוי 'הפרופורציה האלוהית'. אלא שיחס הזהב נמצא כנכון ומתאים לא רק באומנות שעשה האדם, אלא קודם כל בטבע עצמו. כי מעולם הטבע הגיע יחס הזהב והמספר פי לעולם האומנות. ומאז ומתמיד הוא מופיע באדריכלות, במבנים המושלמים והיפים בהיסטוריה, ובאומנות - ברבים מהציורים שבהם יש יחס פרופורציוני בין גדלים שונים.
עמים קדומים כמו היוונים הקדמונים והמצרים הקדמונים התייחסו למלבן הזהב כשיא היופי האסתטי ותכננו לפיו מבנים מהיפים ביותר בעולם העתיק. בין המבנים שבנויים בהקפדה של יחס הזהב או מלבן הזהב, ניתן למצוא את הפירמידות במצרים, הפרתנון שבאקרופוליס של אתונה הטאג' מהאל שבהודו.
הנה מלבן הזהב שיוצר את הספירלות המיוחדות כל כך על פי יחס הזהב:
http://youtu.be/kkGeOWYOFoA
המתמטיקה של יחס הזהב (עברית):
https://youtu.be/co2k2bcZ1h0
ההופעות הרבות של יחס הזהב ומלבן הזהב:
http://youtu.be/0hvD5kLqjuw
והמקומות המפתיעים מסביב שבהם ניתן לפגוש אותו:
https://youtu.be/RqqErDSLtwE?long=yes
מסתבר שאם היו אנשים רבים ומגוונים מכל העולם והתקופות נשאלים איזה מרובע מבין מספר מרובעים שלפניהם הוא היפה והנעים ביותר לעין, היו בוחרים רובם ככולם במלבן הזהב. מלבן הזהב הוא מלבן שהיחס בין אורכו לרוחבו הוא יחס שזכה גם הוא לכינוי יחס הזהב. כשהאורך של מלבן גדול פי בערך 1.618 מהרוחב שלו, מתקיים יחס מושלם ביניהם והוא נקרא מלבן הזהב. מלבן הזהב מוכיח שהיופי הוא אובייקטיבי, כלומר לא תלוי בתקופה, תרבות או אמונה.
כיוון שיחס הזהב הוא כה יפה ומושלם בעיני המתבוננים, הוא זכה לכינוי 'הפרופורציה האלוהית'. אלא שיחס הזהב נמצא כנכון ומתאים לא רק באומנות שעשה האדם, אלא קודם כל בטבע עצמו. כי מעולם הטבע הגיע יחס הזהב והמספר פי לעולם האומנות. ומאז ומתמיד הוא מופיע באדריכלות, במבנים המושלמים והיפים בהיסטוריה, ובאומנות - ברבים מהציורים שבהם יש יחס פרופורציוני בין גדלים שונים.
עמים קדומים כמו היוונים הקדמונים והמצרים הקדמונים התייחסו למלבן הזהב כשיא היופי האסתטי ותכננו לפיו מבנים מהיפים ביותר בעולם העתיק. בין המבנים שבנויים בהקפדה של יחס הזהב או מלבן הזהב, ניתן למצוא את הפירמידות במצרים, הפרתנון שבאקרופוליס של אתונה הטאג' מהאל שבהודו.
הנה מלבן הזהב שיוצר את הספירלות המיוחדות כל כך על פי יחס הזהב:
http://youtu.be/kkGeOWYOFoA
המתמטיקה של יחס הזהב (עברית):
https://youtu.be/co2k2bcZ1h0
ההופעות הרבות של יחס הזהב ומלבן הזהב:
http://youtu.be/0hvD5kLqjuw
והמקומות המפתיעים מסביב שבהם ניתן לפגוש אותו:
https://youtu.be/RqqErDSLtwE?long=yes
מה מיוחד בפסלים שבגן הפסלים של מיניאפוליס?
גן הפסלים של מיניאפוליס (Minneapolis Sculpture Garden), שנפתח בשנת 1988, הוא גן מרהיב וירוק, שתוכנן על ידי אדוארד לרבי בארנס ואדריכלי הנוף קווינל ורוטשילד. הוא משתרע על פני שטח רחב ידיים של 45 דונם.
מדובר בריאה ירוקה בעיר האמריקאית מיניאפוליס, אבל מה שמפורסם בה כל כך הם לא הצמחים והעצים במיוחדים אלא העובדה שזהו גן הפסלים העירוני הגדול ביותר בארצות הברית. הגן גם פתוח בחינם לציבור ולרבים זו הזדמנות להתחבר באופן נגיש יותר לאמנות מודרנית.
בפארק המרשים יש לא פחות מ-40 מיצבים, פסלים קינטיים ופסלים קבועים של אמנים מודרניים מפורסמים מאוד, כמו הנרי מור וקלאוס אולדנבורג. הפסלים הם של מוזיאון לאמנות מודרנית בשם "המרכז לאמנות ווקר" שמעבר לרחוב.
הפסלים פרושים על שטח ירוק ונרחב, בו מצויים גם ברווזים ואף מבנים עטופי ירק. אבל בנוסף לכל אלה, הפארק מכיל גם גן פרחים עם מגוון רחב של צמחים עונתיים ופרחי בר שגבוהים במיוחד בקיץ.
#גשר הכף והדובדבן
גן הפסלים במיניאפוליס ידוע במיוחד במזרקת "גשר הכף והדובדבן" (Spoonbridge And Cherry), או בשפת המקום "ספונברידג' ודובדבן", שיצרו קלאס אולדנבורג וקוז'יה ואן ברוגן. הפסל הזה שהוא גשר נמצא בלב הפארק ומהווה אטרקציה ידועה במיוחד ומפורסמת בעולם כולו.
אבל יש עוד לא מעט יצירות מרתקות בגן הפסלים העירוני הגדול ביותר בארצות הברית. אחד מהם הוא סוס בטרפילד ולא הריק גם התרנגול הכחול הענקי, שהמבקרים נדהמים מגודלו ויופיו.
#פסל ה-LOVE
בפארק גם פסל האהבה של האמן רוברט אינדיאנה, בצורת המילה LOVE. את הפסל הזה אפשר למצוא במקומות רבים ברחבי העולם והוא הפך מזמן לאייקון עולמי, המתנוסס על חולצות, שלטי ענק ופרסומות בעיתונים.
#פסל הנאוטילוס
עוד פסל מיוחד ומעניין בפארק הוא פסל הנאוטילוס של צ'רלס גינבר. את ההשראה לפסל הפלדה הענקי הזה שאב האמן מקונכיית הנאוטילוס בעלת הצורה הלוליינית המושלמת. קונכייה מרתקת זו היא לא רק יפה להפליא, אלא גם אחד מבעלי החיים הימיים העתיקים והמיוחדים ביותר בטבע. הנאוטילוס שרדה מיליוני שנים על פני כדור הארץ ונחשבת לדוגמה קלאסית של סדרת פיבונאצ'י. סיבוב סביב הפסל, יאפשר להבין את קסמו הלולייני ולהבין כיצד הוא מורכב ממספר חללים גדלים והולכים המולחמים זה לזה לאובייקט פיסולי אחד.
הנה גן הפסלים של מיניאפוליס:
https://youtu.be/EJQ0PtuoLL0
הגן מהאוויר:
https://youtu.be/Qit5MVhCHTY
וסרט תיעודי על המקום:
https://youtu.be/U1VCDfQ7UA4?long=yes
גן הפסלים של מיניאפוליס (Minneapolis Sculpture Garden), שנפתח בשנת 1988, הוא גן מרהיב וירוק, שתוכנן על ידי אדוארד לרבי בארנס ואדריכלי הנוף קווינל ורוטשילד. הוא משתרע על פני שטח רחב ידיים של 45 דונם.
מדובר בריאה ירוקה בעיר האמריקאית מיניאפוליס, אבל מה שמפורסם בה כל כך הם לא הצמחים והעצים במיוחדים אלא העובדה שזהו גן הפסלים העירוני הגדול ביותר בארצות הברית. הגן גם פתוח בחינם לציבור ולרבים זו הזדמנות להתחבר באופן נגיש יותר לאמנות מודרנית.
בפארק המרשים יש לא פחות מ-40 מיצבים, פסלים קינטיים ופסלים קבועים של אמנים מודרניים מפורסמים מאוד, כמו הנרי מור וקלאוס אולדנבורג. הפסלים הם של מוזיאון לאמנות מודרנית בשם "המרכז לאמנות ווקר" שמעבר לרחוב.
הפסלים פרושים על שטח ירוק ונרחב, בו מצויים גם ברווזים ואף מבנים עטופי ירק. אבל בנוסף לכל אלה, הפארק מכיל גם גן פרחים עם מגוון רחב של צמחים עונתיים ופרחי בר שגבוהים במיוחד בקיץ.
#גשר הכף והדובדבן
גן הפסלים במיניאפוליס ידוע במיוחד במזרקת "גשר הכף והדובדבן" (Spoonbridge And Cherry), או בשפת המקום "ספונברידג' ודובדבן", שיצרו קלאס אולדנבורג וקוז'יה ואן ברוגן. הפסל הזה שהוא גשר נמצא בלב הפארק ומהווה אטרקציה ידועה במיוחד ומפורסמת בעולם כולו.
אבל יש עוד לא מעט יצירות מרתקות בגן הפסלים העירוני הגדול ביותר בארצות הברית. אחד מהם הוא סוס בטרפילד ולא הריק גם התרנגול הכחול הענקי, שהמבקרים נדהמים מגודלו ויופיו.
#פסל ה-LOVE
בפארק גם פסל האהבה של האמן רוברט אינדיאנה, בצורת המילה LOVE. את הפסל הזה אפשר למצוא במקומות רבים ברחבי העולם והוא הפך מזמן לאייקון עולמי, המתנוסס על חולצות, שלטי ענק ופרסומות בעיתונים.
#פסל הנאוטילוס
עוד פסל מיוחד ומעניין בפארק הוא פסל הנאוטילוס של צ'רלס גינבר. את ההשראה לפסל הפלדה הענקי הזה שאב האמן מקונכיית הנאוטילוס בעלת הצורה הלוליינית המושלמת. קונכייה מרתקת זו היא לא רק יפה להפליא, אלא גם אחד מבעלי החיים הימיים העתיקים והמיוחדים ביותר בטבע. הנאוטילוס שרדה מיליוני שנים על פני כדור הארץ ונחשבת לדוגמה קלאסית של סדרת פיבונאצ'י. סיבוב סביב הפסל, יאפשר להבין את קסמו הלולייני ולהבין כיצד הוא מורכב ממספר חללים גדלים והולכים המולחמים זה לזה לאובייקט פיסולי אחד.
הנה גן הפסלים של מיניאפוליס:
https://youtu.be/EJQ0PtuoLL0
הגן מהאוויר:
https://youtu.be/Qit5MVhCHTY
וסרט תיעודי על המקום:
https://youtu.be/U1VCDfQ7UA4?long=yes
