שלום,
נראה שכבר הכרתם את אאוריקה. בטח כבר גיליתם כאן דברים מדהימים, אולי כבר שאלתם שאלות וקיבלתם תשובות טובות.
נשמח לראות משהו מכם בספר האורחים שלנו: איזו מילה טובה, חוות דעת, עצה חכמה לשיפור או כל מה שיש לכם לספר לנו על אאוריקה, כפי שאתם חווים אותה.
»
«
 מהן שש דרגות של הפרדה?
מהן שש דרגות של הפרדה?
שש דרגות של ההפרדה (Small-world experiment) הוא מושג הקושר בתרבות הפופולרית בין כל שני אנשים בעולם, באמצעות 6 היכרויות בלבד. כלומר, אם תיקח כל שני אנשים בעולם, תגלה שהם קשורים ביניהם, באמצעות מקסימום 5 אנשי קשר.
המושג הזה קשור באופן הדוק ונובע מ"תופעת העולם הקטן", שהגה החוקר סטנלי מילגרם בשנת 1967. מילגרם הראה בניסוי שעשה בנושא, שהמספר החציוני של אנשי קשר הנחוצים כדי ליצור קשר בין כל אמריקאים, תושבי ארצות הברית, הוא 5 מתווכים בלבד.
משמעות שש הדרגות שכאן היא שניתן ליצור קשר בין כל שני אנשים, בעולם כולו, דרך מספר זעום של מתווכים.
ההשערה הזו של מילגרם הייתה שנים רבות שנויה במחלוקת ויש הבודקים אותה כיום במחקרים שמתבצעים ברשתות החברתיות החדשות, שנוצרו מאז מילגרם. באוניברסיטת קולומביה, למשל, נעשה מחקר בנושא שבו נבדקה ההשערה הזו, לראשונה בקנה מידה עולמי. היישום המחקרי נעזר ברשת האינטרנט, תוך בחינת הקשרים בין חברי רשתות חברתיות שונות.
אגב, על בסיס הרעיון של 6 דרגות של הפרדה נולד גם משחק הטריוויה "שש דרגות של קווין בייקון". על המשתתפים במשחק למצוא את הקשר בין כל שחקן לכוכב הקולנוע קווין בייקון, על ידי כך שיאתרו סרטים משותפים שבהם השחקן עם בייקון עצמו, או עם אנשים שהם שיחקו עם בייקון בהפקות שונות, או עם אנשים ששיחקו איתו וכך הלאה...
כך או כך, בשנים האחרונות צבר המונח "שש דרגות של הפרדה" פופולריות רבה בתרבות המודרנית ובעיני רבים הוא מבטא את הביטחון שצפיפותה המתגברת של החברה האנושית הנוכחית, בעידן הכפר הגלובלי, דור ה-Y המחובר תמיד, העולם השטוח, ההגירה הקלה מאי-פעם בין מדינות והגלובליזציה על כל היבטיה - כל אלה הופכים את תושבי העולם קרובים מאוד זה לזה, כמעט ללא גבולות מדיניים, לאומיים או חברתיים כלשהם.
הנה הסבר מתוך הסדרה "החממה" - על שש הדרגות של ההפרדה (עברית):
https://youtu.be/7ZTvjT5Nnz8
עוד הסבר לשש דרגות ההפרדה:
https://youtu.be/LeUhVC8xVQI
על ניסוי שש דרגות של הפרדה:
https://youtu.be/NRWSF1c0Ez0
דוגמה לשש הדרגות של הפרדה:
https://youtu.be/TcxZSmzPw8k
מסתבר שיש לדתיים בישראל משהו דומה שנקרא "דתיים שלובים" (עברית):
https://youtu.be/SrG0gWlNj3Y
וכך גוגל משתמש בשיטת 6 דרגות של ההפרדה (מתורגם):
https://youtu.be/eM1KaaTez0A
 מהי הבדידות שכל כך מעיקה ומה הקשר לסמארטפון?
מהי הבדידות שכל כך מעיקה ומה הקשר לסמארטפון?
בדידות (loneliness) היא אולי הבעיה הכי כואבת בעולם המודרני. היא כבר זכתה לשם "מגפת הבדידות" ומחקר גדול שהושלם באמצע שנת 2024 הראה עד כמה היא אכן כזו.
הבדידות נראית לאנשים בעיה איומה, בעיקר כי החיים האנושיים מגדלים אותנו להיות חלק מחברה וממסגרת של חברים ומשפחה, שמהן אנחנו חלק. מצד שני אנו חיים בעידן שהולך והופך אינדיבידואלי, אישי, עידן של ה"אני" והמימוש העצמי.
והבדידות הכי גדולה, אומרים מחקרים חדשים יחסית, היא דווקא בגילאים צעירים. אם פעם בדידות הייתה יותר בעיה של זקנים, היום שיא הבדידות הוא,החזיקו חזק, בגילאי 18-24.
אם נחזור רגע לפרהיסטוריה, בימי קדם חיו בני האדם במסגרת חברתית. ממש כמו שבעלי חיים רבים הם חלק מלהקה שמגינה עליהם ומבטיחה הישרדות, כך היה גם האדם. החברה הייתה האופציה שלו לחיות ובלעדיה ההישרדות הייתה פשוט בלתי אפשרית. איך יכול היה אדם קדמון להגן על עצמו מפני טורפים, להשיג מזון, להתחמם בחורף ולחיות, כשהוא לגמרי לבדו?
נסו לדמיין חיים לבד ולתת טיפ לאדם קדמון שחי לבדו - מי ישמור לו על האש כשהוא יוצא לצוד חיות או ללקט ירקות? ואיך יכין אוכל בסופו של כל יום כזה, כשהוא מתמוטט מעייפות מיום עמוס פעילות וכל הפיצוציות ליד הנחל עדיין לא הומצאו?
מתחילים להבין? - תחושת הבדידות היא סוג של "כאב חברתי" שפיתחה האבולוציה בבני אדם במהלך דורות רבים, כדי שאנשים לא יתפתו להתנהג באופן לא חברתי ולהביא את עצמם לחיים לבד.
הדחייה החברתית שפגעה בהם לאחר התנהגות לא חברתית, הביאה אנשים באותם ימים לשינוי התנהגות, כדי שלא להיזרק מהמסגרת החברתית שלהם. מי שנזרקו התקשו מאוד להישאר בחיים והלקח לנשארים היה משמעותי - בכדי שלא להפוך לגופה הנאכלת בידי טורפים, כדאי לך מאוד להיות חלק מקבוצה, או בפשטות - טיפוס חברתי.
בימי הביניים של התרבות המערבית היית צמית או פיאודל, אבל תמיד חלק מקבוצה חברתית מוגדרת. בתקופת הרנסאנס שאחריה החל הפרט לקבל משקל משמעותי מאוד והדת הפרוטסטנטית שאך זה נולדה הדגישה את האחריות האישית של האדם. במאות הבאות זה הולך ומתחזק כשהמהפכה התעשייתית מביאה יותר ויותר אנשים לנטוש את חברת הכפר ולעבור לערים גדולות ומנוכרות. שם, לגמרי לבד ובלי המשפחה המורחבת, הם התמקמו עם המשפחה הגרעינית, המצומצמת, ובנו את חייהם.
מכאן נחלשה המסגרת החברתית והמשפחה הרחבה, מה שעתיד עוד יותר להתחזק בעולם המודרני ועוד יותר בעידן האינטרנט והטלפון החכם. כיום, אנשים מתרחקים אלפי קילומטרים זה מזה, כדי לעבוד, ללמוד ולהתחתן. את המשפחה, החמולה והשבט הם נטשו מזמן והתוצאה היא שהרשת החברתית כולה, לא זו המקוונת, נשארת מאחור.
כשעובדים ומקדישים יותר זמן ללימודים, לעניינים רומנטיים ולקריירה, החברים הקרובים שלנו הולכים ומתמעטים. האינטרנט מחליף עוד יותר את החיים והמפגשים עם חברים, בעוד הצ'אט המקוון מחליף את השיחה על בקבוק בירה עם חבר.
כיום, אנו פוגשים פחות ופחות חברים ורובנו הרבה פחות במפגשים של אופן אישי, שאינו מקצועי. בתהליך ארוך אבל מתמיד הופכים המפגשים הללו יותר ויותר נדירים.
זה שלב בחיים שבו המבוגר מתעורר יום אחד ומבין שהוא בודד. בגיל מבוגר למצוא חברים זה הרבה יותר קשה מבעבר. הבדידות הופכת כרונית ובן אדם שמבחינה ביולוגית עדיין זקוק לחברה, חש בודד מתמיד.
זו הסיבה שגם בימינו המודרניים הבדידות מרגישה לנו כל כך כואבת. ככל שהיא כרונית, הבדידות גם הופכת אותנו עוינים וחשדניים יותר ולכן מעמיקה עוד יותר. המוח של הבודד הכרוני מתחיל לעוות את המציאות החברתית שמסביבו. העוינות מחליפה את הנועם והנימוס והאדם הבודד מאבד את הסיכוי לתפיסה נעימה, אפילו של יחסים פשוטים עם הסובבים אותו.
אבל הבדידות לא רק כואבת לנפש. היא גם הורגת. אנשים בודדים נוטים להזדקן הרבה יותר מהר, מחלות הופכות אצלן קטלניות יותר והם חשופים יותר למחלות מוחיות כמו אלצהיימר. המדע והרפואה גילו שממש כמו עישון ועוד יותר מהשמנת יתר, הבדידות הורגת אותנו ואת הזיקנה שלנו ופוגעת בבריאות קשות.
וכך, באופן מדהים אבל אמיתי וכואב, מסתבר שגם בעידן המודרני, הבדידות והדחייה החברתית שאנו יוצרים לנו, מבלי משים ולפחות בראשנו שלנו, הן איומות בשבילנו ומסוכנות להישרדותנו לא פחות מבדידותו של האדם הקדמון, ההוא שנשאר מחוץ למשפחה שבמערה החמימה, עם האש, האוכל והאנשים שהוא לא סובל אבל חולק איתם גנים רבים מדי.
הנה הבדידות והמכניזם שלה (מתורגם):
https://youtu.be/AtCR6P5rsXU
הבדידות פוגעת במוח וביכולות המנטליות:
https://youtu.be/h1DPEFPX_xQ
מחקר שמראה את השפעת הבדידות על המוח:
https://youtu.be/j5PHManr9go
בעידן הקורונה - מה עושים עם הבדידות כשאנחנו בבידוד (עברית):
https://youtu.be/0FZ55qGjaHs
הבדידות וההיסטוריה שלה (מתורגם):
https://youtu.be/n3Xv_g3g-mA?long=yes
והטלפון הנייד המושמץ כל כך הוא לפעמים דווקא מה שמסייע לבודדים (עברית)
https://youtu.be/0ZoEh-x3LvM?long=yes
 למה משתמשים בגרף בועות?
למה משתמשים בגרף בועות?
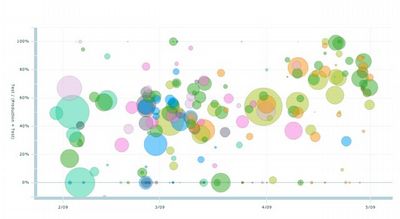
גרף בועות (Bubble Chart) דומה לגרף פיזור בכך שהוא מציג נקודות במערכת צירים עבור שני משתנים, אך מוסיף את גודל הנקודה כמידע נוסף. למעשה, כל "בועה" בגרף היא נקודה שהשטח שלה (או הרדיוס שלה) משקפת משתנה שלישי.
כך ניתן לדוגמה לבנות גרף בועות שבו כל בועה היא מדינה בעולם: מיקום אופקי מייצג בו את התוצר לנפש במדינה, מיקום אנכי מייצג את תוחלת החיים וגודל הבועה מייצג את גודל האוכלוסייה. כך נראה בבת אחת את הקשר בין עושר לאריכות חיים וגם אילו מדינות הן גדולות באוכלוסייה - מדינות עם הרבה תושבים יהיו בועות גדולות ומדינות קטנות יהיו בועות קטנות.
כלומר, באמצעות גרף כזה אפשר להעביר בהצגה דו-ממדית שלושה ממדי מידע: מיקום אופקי (X), מיקום אנכי (Y) וגודל (Z) שניתן לראות באמצעות גודל הבועה.
ואגב, לפעמים משתמשים גם בצבע הבועות כדי לשקף משתנה רביעי, אבל לרוב שני צירים וגודל נותנים כבר תמונה עשירה.
#יתרונות
גרף בועות מאפשר להציג יותר מידע באותה תמונה. הוא מצטיין בהמחשת מערכות נתונים מורכבות שבהן שני משתנים לא מספרים את כל הסיפור. הבועות מוסיפות ממד חדש, אך מבלי לעבור לגרף תלת-ממדי שהוא שקשה יותר לקריאה.
היתרון הוא שניתן לזהות דפוסים שאולי היו נסתרים אם היו מציגים כל פעם רק שני משתנים. אפשר לראות שלושה משתנים קשורים. במקרה המדינות, למשל, ייתכן שנגלה שמדינות עם תוצר גבוה ותוחלת חיים גבוהה הן גם בעלות אוכלוסייה בינונית, ואילו מדינות עם אוכלוסייה עצומה הן לאו דווקא הכי עשירות.
#התאמה
גרף בועות מתאים במיוחד למצבים שבהם יש שלושה משתנים כמותיים לכל פריט ונרצה לבדוק את היחסים ביניהם. הרבה פעמים משתמשים בזה בכלכלה וחברה - למשל להצגת נתוני המדינות כפי שתואר (עושר, בריאות, גודל אוכלוסייה) או להשוואת ביצועי חברות עסקיות (ציר אחד יכול להיות רווח, ציר שני צמיחה וגודל הבועה הוא שווי השוק של החברה).
גם בשיווק אפשר להשתמש בגרף עם בועות. למשל, כשכל בועה היא מוצר. עם ציר X למחיר, ציר Y לשביעות רצון לקוחות וגודל הבועה עבור כמות המכירות. כך ניתן להבין היכן ממוקמים המוצרים בשוק ביחס לשביעות הרצון מהם מול מחירם.
#דוגמאות
בדוגמה אמיתית הוצג על-ידי הנס רוסלינג (Hans Rosling) גרף בועות מפורסם ובו הוא תיאר את התפתחות מדינות העולם. באותו גרף ראו על גבי הגרף בועה לכל מדינה. הציר האופקי היה ההכנסה, הציר האנכי תוחלת החיים, בעוד שגודל הבועה ייצג את גודל האוכלוסייה. כך ניתן היה לראות בקלות את הודו וסין עם אוכלוסיותיהם העצומות, כבועות גדולות ועולות בציר ההכנסה לאורך השנים.
דוגמה יומיומית יותר היא של חנות מקוונת שיכולה לנתח את מוצריה בעזרת גרף בועות. כל בועה מייצגת עבורה מוצר. המיקום האופקי בגרף מייצג את מחירו והמיקום האנכי את דירוג הלקוחות (בכוכבים למשל), בעוד גודל הבועה מייצג את כמות המכירות של אותו מוצר. מבט כזה יכול לגלות שאין קשר בין המחיר לדירוג, אבל כן רואים שמוצרים עם דירוג גבוה נמכרים יותר. זה ייראה בבירור כשבועות גדולות מרוכזות באזורי הדירוג הגבוה בגרף.
הנה הסבר של גרף הבועות:
https://youtu.be/iv0CT5H0yug
עשו ואל תעשו בגרף בועות:
https://youtu.be/Fygi3mQY0Ag
ודוגמאות לגרף בועות בתוכנת Excel:
https://youtu.be/Q1uiytD86OQ
 מה עושים עם תרשים קופסה?
מה עושים עם תרשים קופסה?
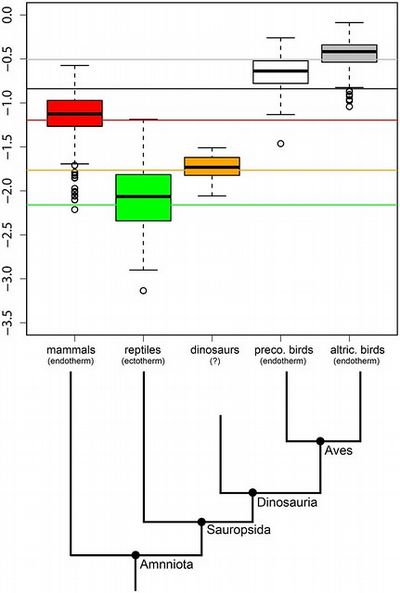
תרשים קופסה ("BoxPlot"), שנקרא גם תרשים תיבה, נותן סיכום חזותי של התפלגות נתונים בעזרת תיבה וקווים תוחמים מחוץ לתיבה, המכונים "שפמים".
תרשים הקופסה מספק 5 דברים על קבוצת הנתונים: המינימום, הרבעון התחתון, החציון, הרבעון העליון והמקסימום.
בתרשים מוצגים בצורה מרוכזת הערכים המרכזיים והפיזור של הנתונים:
#הרבעון התחתון והעליון - אלה גבולות התיבה שהם לרוב הרבעון התחתון והעליון. אלו ערכים שמתחת להם נמצאים 25% ו-75% מהנתונים.
חציון - הקו שבתוך התיבה. זהו החציון (Median), הערך האמצעי של הנתונים.
ערכי המינימום והמקסימום - ערכים שקל לזהות, כי הם מוצגים על ידי קצוות הקווים היוצאים מהקופסה ומכונים "שפמים" (whiskers). השפמים מיקומם בגבול הערכים הקיצוניים, שהם המינימום והמקסימום. ואגב, באנגלית קוראים לתרשימי קופסה גם "תרשימי קופסה ושפמים" (box and whisker plots).
נקודות בודדות מחוץ לטווח השפמים מסמנות ערכים חריגים. כלומר נתונים יוצאי דופן גבוהים או נמוכים במיוחד.
לדוגמה, בתרשים הקופסה יכולים להיות מוצגים ציוני מבחן של שתי כיתות: עבור כל כיתה יש "תיבה" אחת. ניתן לראות מצב בו בכיתה A החציון קצת גבוה מ-70, בעוד בכיתה B החציון הוא סביב 72. פיזור הציונים בכיתה B יכול להיות גדול יותר (התיבה ארוכה יותר וכך גם שפמי כיתה B הארוכים יותר - מה שמראה שהציונים בה מפוזרים על פני טווח רחב יותר). יכולה להיות גם נקודת עיגול מתחת לכיתה B, שמשמעותה היא למשל תלמיד שקיבל ציון חריג נמוך במיוחד לעומת שאר תלמידי כיתתו.
#יתרונות
תרשים קופסה מאפשר השוואה מהירה בין התפלגויות של קבוצות שונות. בגרף אחד אפשר לשים מספר "תיבות" זו ליד זו (כמו בדוגמת שתי הכיתות) ולהבין מיד באיזו קבוצה הערכים באופן כללי גבוהים יותר, איפה הפיזור רחב או צר יותר והאם יש חריגים.
זהו מידע שיהיה קשה לראות בגרפים פשוטים כמו גרף עמודות (שמציגים רק ממוצע או סכום ולא את פיזור הנתונים).
בנוסף, התרשים מספק הרבה מידע במבט מרוכז אחד: ממוצע או חציון, טווח בין-רבעוני (הקופסה), טווח כללי (השפמים) וחריגים, מבלי שנצטרך לראות כל נקודה ונקודה בנפרד.
#התאמה
תרשים הקופסה מתאים במיוחד עבור נתונים כמותיים, כאשר חשוב להבין את הפיזור והמגמה המרכזית שלהם, במיוחד בהשוואה בין כמה קבוצות.
למשל, בציוני מבחן של כמה כיתות שונות, בגבהים של זכרים מול נקבות או בהתפלגות הכנסות בערים שונות - בכל אלו מעניין לא רק מה הממוצע אלא איך הנתונים נפרשים סביבו.
תרשים קופסה שימושי גם בזיהוי ערכים חריגים שיכולים להיות חשובים. כמו, למשל, זיהוי ניסוי מדעי ש"תפס כיוון שונה" משאר התוצאות כי הוא חריג.
#דוגמאות
דוגמה מהחיים: דמיינו בית חולים שמשווה את זמן ההמתנה בחדר המיון בשלושה סניפים שונים. באמצעות תרשים קופסה, יוצג כל סניף בתיבה. אפשר לראות באיזה בית חולים זמן ההמתנה החציוני (חציון) קצר ביותר ובאיזה הפיזור גדול.
ייתכן שבבית חולים אחד לרוב ממתינים 10-20 דקות (תיבה קטנה), בעוד שבאחר הזמנים מגוונים ונפרשים מ-5 דקות ועד שעה (תיבה ושפמים גדולים יותר). מידע כזה עוזר לזהות איפה השירות עקבי ומהיר יותר.
עוד תרשים לדוגמה יכול להיות באמצעות Box Plot של ציוני שתי כיתות (כיתה A וכיתה B). הקו האדום בכל תיבה הוא החציון, הקופסה מראה את טווח הציונים האמצעי, והנקודות (כמו עיגול לבן) הן ערכים חריגים.
הנה הסבר של תרשים הקופסה:
https://youtu.be/Ck5HMTnvfw0
דוגמה שימושית לתרשים כזה:
https://youtu.be/b2C9I8HuCe4
חמשת הנקודות העיקריות בתרשים הקופסה:
https://youtu.be/E7ewAxluyt0
הנתונים שמראה תרשים קופסה:
https://youtu.be/EVm1NhGod1w
כך תקראו תרשים קופסה:
https://youtu.be/fHLhBnmwUM0
ותרשים קופסה בתוכנת אקסל:
https://youtu.be/f7rkB7c-zDw
 מה מציגה מפת חום?
מה מציגה מפת חום?
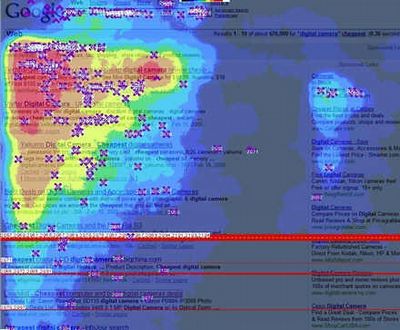
מפת חום (Heatmap) מציגה טבלה של ערכים בשני ממדים כאשר הערכים מיוצגים כצבעים.
כלומר, יש לנו ציר אופקי וציר אנכי (למשל, ימים ושעות, או פריטים שונים מול תכונות שונות), ובנקודת המפגש של כל שני פרמטרים יש ערך מספרי שמיוצג על ידי צבע.
במפת חום לרוב משתמשים בסקאלה צבעונית. למשל, מכחול דרך צהוב עד אדום, כדי לציין מערך ערכים נמוכים עד גבוהים.
היתרון הוא שבמבט אחד ניתן לאתר דפוסים: אזורים חמים (בצבע בולט כמו אדום) לעומת קרים (כחול או צבע כהה) שמראים איפה הערכים גבוהים או נמוכים במיוחד.
לדוגמה, דמיינו heatmap שבו ניתן לראות את עומס המבקרים בחנות לאורך הימים והשעות. כל שורה מייצגת יום בשבוע וכל עמודה שעה ביום. בעוד הצבע הלבן-צהוב מצביע על שעות שיא עם הרבה לקוחות (צהרי היום ובערב), השחור-אדמדם מצביע על שעות שקטות (למשל באמצע הלילה או מוקדם בבוקר).
כך ניתן לראות במבט מהיר שבסופי שבוע (שבת-ראשון) בצהריים יש צבע בהיר מאוד, כלומר החנות עמוסה אז במיוחד.
#יתרונות
מפת חום מצטיינת ביכולת להראות הרבה מידע בתמונה אחת באופן אינטואיטיבי. היא טובה בזיהוי תבניות, כי העין שלנו מיד נמשכת לאזורים בולטים בצבעם. למשל, אם נשתמש במפת חום להצגת ציוני תלמידים במקצועות שונים (שורות תלמידים, עמודות מקצועות, וצבע = ציון), נוכל מיד להבחין באילו מקצועות כיתה שלמה חזקה (מה שייראה בצורת עמודה בולטת בצבע מסוים) או האם תלמיד ספציפי בולט לרעה או לטובה (שורה מסוימת עם צבעים קיצוניים).
#התאמה
מפת החום מתאימה במיוחד עבור נתונים בעלי שני ממדים של קטגוריות או רצף, כשעבור כל צירוף שלהם יש ערך מספרי.
זה יכול להיות זמנים מול מקומות (כמו בדוגמת החנות: לכל יום ושעה יש מספר של לקוחות), או אנשים מול תכונות (למשל, טבלת תלמידים וציוניהם בכמה מקצועות), או אפילו מטריצה של מתאם בין משתנים (כשרוצים לראות אילו משתנים קשורים, עם ערכים גבוהים בצבע בולט).
מפת חום שימושית גם למדעני נתונים בתחומים כמו ביולוגיה ובינה מלאכותית, כדי להציג מטריצות גדולות בצורה שקל לקלוט (כמו "DNA Microarray" בביולוגיה, שמציג ביטויי גנים שונים כדוגמאות צבע).
#דוגמאות
דוגמה מהחיים: רשת חברתית יכולה להציג למנהלי הקהילה מפה צבעונית של פעילות המשתמשים לפי שעה ויום: למשל, הצבעים יראו שבשעות הערב של סוף השבוע הפעילות באתר בשיאה (צבע חם מאוד) ואילו בשעות בוקר של אמצע השבוע הפעילות נמוכה (צבע קר).
דוגמה נוספת: אפליקציית תחבורה ציבורית עשויה להראות Heatmap של עומס נוסעים בתחנות שונות לאורך היום. כך ניתן לראות באילו תחנות ושעות יש עומס גדול (אדום), מה שעוזר בהקצאת משאבים כמו אוטובוסים נוספים בזמן הנכון.
מהי מפת חום?
https://youtu.be/Q3XFj3zJBuE
מפת חום בגוגל Sheet:
https://youtu.be/RuvbI3QcsFo
ליצור מפת חום בתוכנת אקסל:
https://youtu.be/4Ftu8ay4UKc
הרצאונת על מהי מפת חום ואיך להשתמש בה:
https://youtu.be/stgf2CfiXr4
ומפת חום מורכבת במיוחד:
https://youtu.be/NFbiSX6PYXo
 מהו גרף עמודות ולמה הוא טוב?
מהו גרף עמודות ולמה הוא טוב?
גרף עמודות (Bar Chart) הוא גרף השוואתי, עם ציר אחד בלבד, המציג השוואה בין קטגוריות שונות בעזרת מלבנים או עמודות שכל אחד מהם מייצג קטגוריה.
גובה כל עמודה (או אורך, אם העמודות אופקיות) מראה לנו כמה גדול הערך של אותה קטגוריה, למשל שכיחות של משהו, כמה ממנו יש. למשל, גרף של מספר תושבים בערים שונות יראה לנו עמודות שונות, שכל אחת מהן מציגה את גודל האוכלוסיה בעיר המסוימת, את שכיחות התושבים בה.
ערך גבוה מיוצג על-ידי עמודה גבוהה וערך נמוך על-ידי עמודה נמוכה. כלומר הגרף מסוג זה הוא פשוט לקריאה: ניתן מיד לראות בו בעמודות מי בין הקטגוריות היא "הכי גדולה" ומי "הכי קטנה", מי יותר ומי פחות.
לדוגמה, אפשר להשתמש בגרף עמודות כדי להציג את מספר התלמידים בכל כיתה בשכבה, כאשר לכל כיתה יש עמודה בגובה המתאים למספר התלמידים בה.
#יתרונות
גרף עמודות מצטיין בהשוואת גדלים בין פריטים או קבוצות שונות בצורה ישירה. בניגוד לגרף עוגה, שבו קשה להשוות בדיוק גדלים של פרוסות, כאן אפשר לראות בבירור ובמדויק איזו עמודה גבוהה יותר, גם אם ההפרשים לעתים זעירים.
גרף העמודות עדיף לעיתים גם על גרף קו, כשהנתונים אינם רציפים אלא מחולקים לקטגוריות נפרדות (למשל סוגי מוצרים, ערים, קבוצות גיל וכדומה).
#מתי?
גרף העמודות מתאים במיוחד עבור נתונים קטגוריים - כלומר נתונים המחולקים לקבוצות או לסוגים ברורים. גרף כזה מתאים להראות כמויות, סכומים או מספר פריטים בכל קטגוריה.
הגרף יעיל גם להצגת נתונים של תקופות (חודשים, שנים) כשרוצים להשוות תקופה לתקופה ולא בהכרח להראות מגמה רציפה.
#דוגמאות
למשל, השוואת כמות הגשמים בחודשי השנה באמצעות עמודות, כשלכל חודש עמודה המציגה את כמות המשקעים בו.
דוגמה נוספת: גרף עמודות יכול להראות כמה משתמשים יש לכל רשת חברתית (פייסבוק, אינסטגרם, טוויטר וכו'), כאשר כל רשת מיוצגת בעמודה. כך רואים איזו רשת היא בעלת מספר המשתמשים הגדול ביותר בצורה ברורה.
הנה גרף עמודות:
https://youtu.be/WTVdncVCvKo
גרף עמודות המציג מספר ערכים השוואתיים מטבלת שכיחות (עברית):
https://youtu.be/ZrBw7vTRsUs
דוגמה לגרף עמודות אופקי:
https://youtu.be/wlEQ6h9ilUU
ותבנית לילדים ליצירת דיאגרמת עמודות, גרף עמודות (עברית):
https://youtu.be/RjYKvcvlies
 איך היסטוגרמה מראה התפלגויות?
איך היסטוגרמה מראה התפלגויות?
היסטוגרמה (Histogram) דומה במראה לגרף עמודות, אך היא משרתת מטרה שונה: היא מראה התפלגות של נתונים רציפים. ציר אחד (בדרך כלל אופקי) מחולק ל"טווחים" או "אשכולות" של ערכים (בין X ל-Y, Y ל-Z, וכו') והציר האחר מראה כמה נתונים נופלים בכל טווח כזה.
כל עמודה בהיסטוגרמה מייצגת את מספר המקרים או התצפיות שהתגלו בטווח ערכים מסוים. כך למעשה ההיסטוגרמה נותנת מושג על צורת ההתפלגות – האם רוב הנתונים מרוכזים בטווח צר, פזורים באופן אחיד, או אולי יש שני "שיאים" וכו'.
אם נאסוף, לדוגמה, את ציוני המבחן של 100 תלמידים, נוכל ליצור היסטוגרמה שבה כל עמודה מראה כמה תלמידים קיבלו ציון בטווח מסוים (נגיד 50-60, 60-70, 70-80, וכו'). כך אפשר לראות האם רוב הכיתה קיבלה ציונים גבוהים, נמוכים, או שהתפלגו באופן שווה.
#יתרונות
היסטוגרמה מצטיינת בהצגת התפלגות ערכים – משהו שגרף עמודות רגיל אינו עושה, כי גרף עמודות מציג כל קטגוריה בנפרד ולא טווח רציף.
בעזרת היסטוגרמה אפשר לזהות במהירות מאפיינים של הנתונים כמו שכיחות (כמה פעמים ערכים מופיעים בטווח מסוים), האם יש הטיה לכיוון גבוה או נמוך והאם הנתונים מרוכזים סביב ערך מרכזי או מפוזרים.
כך, למשל, אפשר לראות אם יש "זנב ארוך" – כלומר מעט ערכים רחוקים מהמרכז (מה שיראה כעמודה בודדת רחוקה מהשאר).
#התאמה
היסטוגרמה מתאימה במיוחד עבור נתונים מספריים רציפים בכמות גדולה, כאשר רוצים להבין את הצורה הכללית שלהם.
כל מצב שבו יש מדידה כמותית להרבה פרטים - ציוני תלמידים, גבהים של אנשים, משך זמן שלוקח לאנשים לבצע משימה, טמפרטורות יומיות בחודש – יתאים להיסטוגרמה.
מה שכן, חשוב שלנתונים יהיה טווח ערכים רחב מספיק כדי לחלק לטווחים (Bins) ולהפיק תובנות מצורת ההצטברות שלהם.
#דוגמאות
דוגמה מהחיים היא של מורה שיכול להכין היסטוגרמה של ציוני הבחינה בכיתה כדי לראות את פיזור הציונים. הציר האופקי הוא טווחי ציונים, בעוד הציר האנכי הוא מספר התלמידים בכל טווח. כך ניתן לבחון האם יש שתי פסגות (האם למשל קבוצה גדולה קיבלה ציונים נמוכים וקבוצה גדולה אחרת ציונים גבוהים) או שהציונים מרוכזים סביב ציון ביניים.
דוגמה נוספת: היסטוגרמה של גילאי תושבי עיר – ציר אופקי טווחי גיל (0-9, 10-19, 20-29 וכו') והציר האנכי מספר התושבים בכל טווח. כך העירייה יכולה לראות אם יש הרבה צעירים, הרבה מבוגרים וכו', דברים שיכולים להשפיע על תכנון וסוג השירותים לתושבים.
מהי היסטוגרמה, מתי להשתמש בה ואיך?
https://youtu.be/haJyaQObNwU
היסטוגרמה בעולם ההשקעות:
https://youtu.be/Xv8gh2exXeE
מה ההבדל בין היסטוריה לגרף עמודות?
https://youtu.be/JsEwJD1mYpU
היסטוגרמה? - מתי להשתמש באיזה גרף?
https://youtu.be/yrTB5JSQPqY
כך תבנו היסטוגרמה:
https://youtu.be/fHX7myclXyk
 מדוע נקראת מידת המהירות בים "קשר ימי"?
מדוע נקראת מידת המהירות בים "קשר ימי"?
בנהיגה בכלי רכב יבשתיים, כמו אופניים או מכונית, המהירות נמדדת בקילומטרים או במיילים לשעה. אבל כל מי שהתנסה או קרא על שיט באוניה או ביכטה, שמע ודאי את המונח קֶשֶר (Knot), או קשר ימי, המשמש למדידת המהירות בים.
לרשות ספנים בספינות עתיקות לא היו אמצעים כמו מפות מודרניות או מתקני ניווט מבוססי GPS. הם נזקקו לשיטה שתסייע להם לזהות את כיוון השיט הרצוי וכמה זמן עליהם לשוט עד שיגיעו לשם. מדידת מהירות הנסיעה של ספינה הייתה הכרחית כי ללא כלי שיאפשר אותה עלולים היו צוותי הספינות הללו להתרחק מהמסלול ולאבד את חייהם. מדידת המהירות של הספינה היה הכרחי כדי לנווט ולדעת מתי היא תגיע אל היעד.
המילה קשר מזכירה קשר בחבל ולמעשה זה העניין. כי הקֶשֶר הימי, הוא יחידת המדידה של המהירות הימית והיא קרויה על שם השיטה הקדומה למדידת מהירות של אוניות.
במאה ה-17, לפני מאות שנים, העלו ספנים אלמונים, בעלי יוזמה וכושר המצאה, רעיון למדידת המהירות. הם לקחו חבלים ארוכים וקשרו בהם קשרים, במרווחים מדויקים של 14.4 מטר. את החבלים הם שילבו במכשיר פשוט ביותר, שממנו יצאה חתיכת החבל עם הקשרים ובקצה שלה היא חוברה למשקולת עץ בצורת טריז. את טריז העץ המחובר לחבל השליכו אל המים, כשקצהו השני של החבל, זה עם המכשיר, נשאר מחובר לספינה.
וכך, תוך כדי שיט, שחררו המלחים את החבלים הללו. הם השתמשו בשעון חול למדידת פרק זמן קבוע, מה שנקרא "טיימר" (Timer). וכך ספרו המלחים כמה קשרים עברו באצבעותיהם בפרק הזמן המוקצב לשעון החול להשלים ירידה של כל החול. כך נהגו אז להכפיל את מספר הקשרים בשעה ולקבל את המהירות ב"קשר ימי".
כך נהגו הספנים כל הזמן לחשב את מהירות האוניה ונעשה חישוב של הממוצע שיאמר כמה מהר היא שטה. משידעו את מהירות הספינה הם חישבו בכל יום את המיקום שלהם בים וכמה זמן נותר להם עד שיגיעו ליעד שאליו הם מתכוונים להגיע.
כיום יש אמצעים חדשניים ומדויקים במיוחד למדידת מהירות הספינה. ספנים משתמשים ב-GPS, המבוסס על מדידת מיקום סופר מדויקת, שמתבצעת בעזרת רשת לוויינים וחיישני אולטרה סאונד. ועדיין, משתמשים גם היום במושג קילומטר הימי וגם בעולם התעופה. גם מטוסים מודדים את מהירותם בקשרים ובמיילים ימיים המבוססים על היקף כדור הארץ.
מדהים שכך הוליד מכשיר פשוט וחכם, שהומצא במאה ה-17, את המושגים המקובלים עד היום למדידת מהירות שיט ואף טיסה. קשר היא יחידה ששווה ל-1 מייל ימי לשעה. בקילומטרים היא בערך 1.852 קילומטר לשעה. קילומטר ימי מבוסס למעשה על היקף כדור הארץ. הוא שווה בדיוק לדקה של קו רוחב.
הנה מדידה של מהירות ומרחק הספינה באמצעות קשר:
http://youtu.be/LZY3FJGG_gQ?t=22s
והסבר על מדידת המהירות באמצעות קשרים בחבל:
https://youtu.be/RtvfYJFhYEg
 מה זה גרף ולמה צריך גרפים?
מה זה גרף ולמה צריך גרפים?
גְּרָף (Graph Data), או גרף נתונים, הוא תיאור שבדרך כלל הוא דו-ממדי של מספר פרטי מידע המקושרים ביניהם על ידי יחסים כלשהם.
הגרף ישמש בדרך כלל להצגה חזותית של מידע כמותי. הוא מאפשר השוואה של הפריטים השונים זה לזה, בעזרת יחידות המידה שבדרך כלל מוצגות על הציר או על שני צירי הגרף. כי גם אם גרפים עתירי נתונים יוצגו לעתים עם מערכת צירים תלת-ממדית, בדרך כלל הם יוצגו בגרפים המבוססים על מערכת צירים דו-ממדית.
הציר האופקי, הציר שממש כמו האופק שאליו אנו מביטים נמתח לרוחב, יציג בדרך כלל את המשתנה. אם למשל נציג גרף של פופולריות של מוצר לאורך תקופה מסוימת, אז הציר האופקי יציג את הזמן, למשל את החודשים בשנה האחרונה.
הציר האנכי, העומד, יציג את הפונקציה. למשל בגרף של פופולריות המוצר בשנה האחרונה הציר הזה יציג את הפופולריות שלו, הפונקציה של המשתנה - כמה המוצר נמכר, או מה אחוז הנשאלים שאהבו את המוצר בסקר החודשי.
#למה צריך את זה?
גדולתו של הגרף היא בייצוג ויזואלי והשוואתי, באופן מופשט וללא מידע מיותר. כל זה לגבי קבוצת הפריטים או הנתונים, כשכולם מקושרים ביניהם באופן כלשהו.
יתרונם הגדול של הגרפים הוא בקלות ובמהירות של קליטת המידע מהם. גרף טוב יאפשר זיהוי מהיר של הקשר בין הנתונים והיחסים ביניהם, לעתים גם כולל המגמות שניתן לזהות בהם והחריגות שבין הנתונים.
#סוגי גרפים
ישנם כמה סוגי גרפים, כשלכל סוג יש יתרונות משלו ושימושים מתאימים לסוג המידע שהוא מציג היטב לצרכי ויזואליזציה של נתונים.
הגרפים הבולטים, השכיחים והשימושיים ביותר הם גרף עמודות, גרף קו, גרף עוגה, היסטוגרמה, גרף פיזור, תרשים קופסה (Box Plot), גרף בועות, גרף רציף, גרף נרות יפניים (גרף קו המציג את המדידות בניתוח טכני באופן משוכלל יותר מנקודות על הקו) ומפת חום (Heatmap) שהיא מעט שונה אבל נחשבת גם היא לסוג של גרף.
למחקר תאורטי נרחב זכו הגרפים במסגרת תורת הגרפים. ישנם סוגי גרפים שונים. להיכרות איתם ראו את תגית "סוגי גרפים".
הנה הסבר לילדים על מה זה גרף:
https://youtu.be/LW7I0Skjaew
כמה מסוגי הגרפים שמשתמשים בהם:
https://youtu.be/bmY28wdGL9M
איך יודעים באיזה גרף להשתמש בכל הקשר?
https://youtu.be/o7F-tbBl_hA
גרף נתונים בקו שמדגים את השינויים לאורך זמן (עברית):
https://youtu.be/siBhC7scAdQ
כך אפשר לזהות הטעיה באמצעות גרף (מתורגם):
https://youtu.be/E91bGT9BjYk
וגרף הנרות היפניים בעולם המסחר במניות (עברית):
https://youtu.be/FPZbtNtbMtc?long=yes

שש דרגות של ההפרדה (Small-world experiment) הוא מושג הקושר בתרבות הפופולרית בין כל שני אנשים בעולם, באמצעות 6 היכרויות בלבד. כלומר, אם תיקח כל שני אנשים בעולם, תגלה שהם קשורים ביניהם, באמצעות מקסימום 5 אנשי קשר.
המושג הזה קשור באופן הדוק ונובע מ"תופעת העולם הקטן", שהגה החוקר סטנלי מילגרם בשנת 1967. מילגרם הראה בניסוי שעשה בנושא, שהמספר החציוני של אנשי קשר הנחוצים כדי ליצור קשר בין כל אמריקאים, תושבי ארצות הברית, הוא 5 מתווכים בלבד.
משמעות שש הדרגות שכאן היא שניתן ליצור קשר בין כל שני אנשים, בעולם כולו, דרך מספר זעום של מתווכים.
ההשערה הזו של מילגרם הייתה שנים רבות שנויה במחלוקת ויש הבודקים אותה כיום במחקרים שמתבצעים ברשתות החברתיות החדשות, שנוצרו מאז מילגרם. באוניברסיטת קולומביה, למשל, נעשה מחקר בנושא שבו נבדקה ההשערה הזו, לראשונה בקנה מידה עולמי. היישום המחקרי נעזר ברשת האינטרנט, תוך בחינת הקשרים בין חברי רשתות חברתיות שונות.
אגב, על בסיס הרעיון של 6 דרגות של הפרדה נולד גם משחק הטריוויה "שש דרגות של קווין בייקון". על המשתתפים במשחק למצוא את הקשר בין כל שחקן לכוכב הקולנוע קווין בייקון, על ידי כך שיאתרו סרטים משותפים שבהם השחקן עם בייקון עצמו, או עם אנשים שהם שיחקו עם בייקון בהפקות שונות, או עם אנשים ששיחקו איתו וכך הלאה...
כך או כך, בשנים האחרונות צבר המונח "שש דרגות של הפרדה" פופולריות רבה בתרבות המודרנית ובעיני רבים הוא מבטא את הביטחון שצפיפותה המתגברת של החברה האנושית הנוכחית, בעידן הכפר הגלובלי, דור ה-Y המחובר תמיד, העולם השטוח, ההגירה הקלה מאי-פעם בין מדינות והגלובליזציה על כל היבטיה - כל אלה הופכים את תושבי העולם קרובים מאוד זה לזה, כמעט ללא גבולות מדיניים, לאומיים או חברתיים כלשהם.
הנה הסבר מתוך הסדרה "החממה" - על שש הדרגות של ההפרדה (עברית):
https://youtu.be/7ZTvjT5Nnz8
עוד הסבר לשש דרגות ההפרדה:
https://youtu.be/LeUhVC8xVQI
על ניסוי שש דרגות של הפרדה:
https://youtu.be/NRWSF1c0Ez0
דוגמה לשש הדרגות של הפרדה:
https://youtu.be/TcxZSmzPw8k
מסתבר שיש לדתיים בישראל משהו דומה שנקרא "דתיים שלובים" (עברית):
https://youtu.be/SrG0gWlNj3Y
וכך גוגל משתמש בשיטת 6 דרגות של ההפרדה (מתורגם):
https://youtu.be/eM1KaaTez0A

בדידות (loneliness) היא אולי הבעיה הכי כואבת בעולם המודרני. היא כבר זכתה לשם "מגפת הבדידות" ומחקר גדול שהושלם באמצע שנת 2024 הראה עד כמה היא אכן כזו.
הבדידות נראית לאנשים בעיה איומה, בעיקר כי החיים האנושיים מגדלים אותנו להיות חלק מחברה וממסגרת של חברים ומשפחה, שמהן אנחנו חלק. מצד שני אנו חיים בעידן שהולך והופך אינדיבידואלי, אישי, עידן של ה"אני" והמימוש העצמי.
והבדידות הכי גדולה, אומרים מחקרים חדשים יחסית, היא דווקא בגילאים צעירים. אם פעם בדידות הייתה יותר בעיה של זקנים, היום שיא הבדידות הוא,החזיקו חזק, בגילאי 18-24.
אם נחזור רגע לפרהיסטוריה, בימי קדם חיו בני האדם במסגרת חברתית. ממש כמו שבעלי חיים רבים הם חלק מלהקה שמגינה עליהם ומבטיחה הישרדות, כך היה גם האדם. החברה הייתה האופציה שלו לחיות ובלעדיה ההישרדות הייתה פשוט בלתי אפשרית. איך יכול היה אדם קדמון להגן על עצמו מפני טורפים, להשיג מזון, להתחמם בחורף ולחיות, כשהוא לגמרי לבדו?
נסו לדמיין חיים לבד ולתת טיפ לאדם קדמון שחי לבדו - מי ישמור לו על האש כשהוא יוצא לצוד חיות או ללקט ירקות? ואיך יכין אוכל בסופו של כל יום כזה, כשהוא מתמוטט מעייפות מיום עמוס פעילות וכל הפיצוציות ליד הנחל עדיין לא הומצאו?
מתחילים להבין? - תחושת הבדידות היא סוג של "כאב חברתי" שפיתחה האבולוציה בבני אדם במהלך דורות רבים, כדי שאנשים לא יתפתו להתנהג באופן לא חברתי ולהביא את עצמם לחיים לבד.
הדחייה החברתית שפגעה בהם לאחר התנהגות לא חברתית, הביאה אנשים באותם ימים לשינוי התנהגות, כדי שלא להיזרק מהמסגרת החברתית שלהם. מי שנזרקו התקשו מאוד להישאר בחיים והלקח לנשארים היה משמעותי - בכדי שלא להפוך לגופה הנאכלת בידי טורפים, כדאי לך מאוד להיות חלק מקבוצה, או בפשטות - טיפוס חברתי.
בימי הביניים של התרבות המערבית היית צמית או פיאודל, אבל תמיד חלק מקבוצה חברתית מוגדרת. בתקופת הרנסאנס שאחריה החל הפרט לקבל משקל משמעותי מאוד והדת הפרוטסטנטית שאך זה נולדה הדגישה את האחריות האישית של האדם. במאות הבאות זה הולך ומתחזק כשהמהפכה התעשייתית מביאה יותר ויותר אנשים לנטוש את חברת הכפר ולעבור לערים גדולות ומנוכרות. שם, לגמרי לבד ובלי המשפחה המורחבת, הם התמקמו עם המשפחה הגרעינית, המצומצמת, ובנו את חייהם.
מכאן נחלשה המסגרת החברתית והמשפחה הרחבה, מה שעתיד עוד יותר להתחזק בעולם המודרני ועוד יותר בעידן האינטרנט והטלפון החכם. כיום, אנשים מתרחקים אלפי קילומטרים זה מזה, כדי לעבוד, ללמוד ולהתחתן. את המשפחה, החמולה והשבט הם נטשו מזמן והתוצאה היא שהרשת החברתית כולה, לא זו המקוונת, נשארת מאחור.
כשעובדים ומקדישים יותר זמן ללימודים, לעניינים רומנטיים ולקריירה, החברים הקרובים שלנו הולכים ומתמעטים. האינטרנט מחליף עוד יותר את החיים והמפגשים עם חברים, בעוד הצ'אט המקוון מחליף את השיחה על בקבוק בירה עם חבר.
כיום, אנו פוגשים פחות ופחות חברים ורובנו הרבה פחות במפגשים של אופן אישי, שאינו מקצועי. בתהליך ארוך אבל מתמיד הופכים המפגשים הללו יותר ויותר נדירים.
זה שלב בחיים שבו המבוגר מתעורר יום אחד ומבין שהוא בודד. בגיל מבוגר למצוא חברים זה הרבה יותר קשה מבעבר. הבדידות הופכת כרונית ובן אדם שמבחינה ביולוגית עדיין זקוק לחברה, חש בודד מתמיד.
זו הסיבה שגם בימינו המודרניים הבדידות מרגישה לנו כל כך כואבת. ככל שהיא כרונית, הבדידות גם הופכת אותנו עוינים וחשדניים יותר ולכן מעמיקה עוד יותר. המוח של הבודד הכרוני מתחיל לעוות את המציאות החברתית שמסביבו. העוינות מחליפה את הנועם והנימוס והאדם הבודד מאבד את הסיכוי לתפיסה נעימה, אפילו של יחסים פשוטים עם הסובבים אותו.
אבל הבדידות לא רק כואבת לנפש. היא גם הורגת. אנשים בודדים נוטים להזדקן הרבה יותר מהר, מחלות הופכות אצלן קטלניות יותר והם חשופים יותר למחלות מוחיות כמו אלצהיימר. המדע והרפואה גילו שממש כמו עישון ועוד יותר מהשמנת יתר, הבדידות הורגת אותנו ואת הזיקנה שלנו ופוגעת בבריאות קשות.
וכך, באופן מדהים אבל אמיתי וכואב, מסתבר שגם בעידן המודרני, הבדידות והדחייה החברתית שאנו יוצרים לנו, מבלי משים ולפחות בראשנו שלנו, הן איומות בשבילנו ומסוכנות להישרדותנו לא פחות מבדידותו של האדם הקדמון, ההוא שנשאר מחוץ למשפחה שבמערה החמימה, עם האש, האוכל והאנשים שהוא לא סובל אבל חולק איתם גנים רבים מדי.
הנה הבדידות והמכניזם שלה (מתורגם):
https://youtu.be/AtCR6P5rsXU
הבדידות פוגעת במוח וביכולות המנטליות:
https://youtu.be/h1DPEFPX_xQ
מחקר שמראה את השפעת הבדידות על המוח:
https://youtu.be/j5PHManr9go
בעידן הקורונה - מה עושים עם הבדידות כשאנחנו בבידוד (עברית):
https://youtu.be/0FZ55qGjaHs
הבדידות וההיסטוריה שלה (מתורגם):
https://youtu.be/n3Xv_g3g-mA?long=yes
והטלפון הנייד המושמץ כל כך הוא לפעמים דווקא מה שמסייע לבודדים (עברית)
https://youtu.be/0ZoEh-x3LvM?long=yes

גרף בועות (Bubble Chart) דומה לגרף פיזור בכך שהוא מציג נקודות במערכת צירים עבור שני משתנים, אך מוסיף את גודל הנקודה כמידע נוסף. למעשה, כל "בועה" בגרף היא נקודה שהשטח שלה (או הרדיוס שלה) משקפת משתנה שלישי.
כך ניתן לדוגמה לבנות גרף בועות שבו כל בועה היא מדינה בעולם: מיקום אופקי מייצג בו את התוצר לנפש במדינה, מיקום אנכי מייצג את תוחלת החיים וגודל הבועה מייצג את גודל האוכלוסייה. כך נראה בבת אחת את הקשר בין עושר לאריכות חיים וגם אילו מדינות הן גדולות באוכלוסייה - מדינות עם הרבה תושבים יהיו בועות גדולות ומדינות קטנות יהיו בועות קטנות.
כלומר, באמצעות גרף כזה אפשר להעביר בהצגה דו-ממדית שלושה ממדי מידע: מיקום אופקי (X), מיקום אנכי (Y) וגודל (Z) שניתן לראות באמצעות גודל הבועה.
ואגב, לפעמים משתמשים גם בצבע הבועות כדי לשקף משתנה רביעי, אבל לרוב שני צירים וגודל נותנים כבר תמונה עשירה.
#יתרונות
גרף בועות מאפשר להציג יותר מידע באותה תמונה. הוא מצטיין בהמחשת מערכות נתונים מורכבות שבהן שני משתנים לא מספרים את כל הסיפור. הבועות מוסיפות ממד חדש, אך מבלי לעבור לגרף תלת-ממדי שהוא שקשה יותר לקריאה.
היתרון הוא שניתן לזהות דפוסים שאולי היו נסתרים אם היו מציגים כל פעם רק שני משתנים. אפשר לראות שלושה משתנים קשורים. במקרה המדינות, למשל, ייתכן שנגלה שמדינות עם תוצר גבוה ותוחלת חיים גבוהה הן גם בעלות אוכלוסייה בינונית, ואילו מדינות עם אוכלוסייה עצומה הן לאו דווקא הכי עשירות.
#התאמה
גרף בועות מתאים במיוחד למצבים שבהם יש שלושה משתנים כמותיים לכל פריט ונרצה לבדוק את היחסים ביניהם. הרבה פעמים משתמשים בזה בכלכלה וחברה - למשל להצגת נתוני המדינות כפי שתואר (עושר, בריאות, גודל אוכלוסייה) או להשוואת ביצועי חברות עסקיות (ציר אחד יכול להיות רווח, ציר שני צמיחה וגודל הבועה הוא שווי השוק של החברה).
גם בשיווק אפשר להשתמש בגרף עם בועות. למשל, כשכל בועה היא מוצר. עם ציר X למחיר, ציר Y לשביעות רצון לקוחות וגודל הבועה עבור כמות המכירות. כך ניתן להבין היכן ממוקמים המוצרים בשוק ביחס לשביעות הרצון מהם מול מחירם.
#דוגמאות
בדוגמה אמיתית הוצג על-ידי הנס רוסלינג (Hans Rosling) גרף בועות מפורסם ובו הוא תיאר את התפתחות מדינות העולם. באותו גרף ראו על גבי הגרף בועה לכל מדינה. הציר האופקי היה ההכנסה, הציר האנכי תוחלת החיים, בעוד שגודל הבועה ייצג את גודל האוכלוסייה. כך ניתן היה לראות בקלות את הודו וסין עם אוכלוסיותיהם העצומות, כבועות גדולות ועולות בציר ההכנסה לאורך השנים.
דוגמה יומיומית יותר היא של חנות מקוונת שיכולה לנתח את מוצריה בעזרת גרף בועות. כל בועה מייצגת עבורה מוצר. המיקום האופקי בגרף מייצג את מחירו והמיקום האנכי את דירוג הלקוחות (בכוכבים למשל), בעוד גודל הבועה מייצג את כמות המכירות של אותו מוצר. מבט כזה יכול לגלות שאין קשר בין המחיר לדירוג, אבל כן רואים שמוצרים עם דירוג גבוה נמכרים יותר. זה ייראה בבירור כשבועות גדולות מרוכזות באזורי הדירוג הגבוה בגרף.
הנה הסבר של גרף הבועות:
https://youtu.be/iv0CT5H0yug
עשו ואל תעשו בגרף בועות:
https://youtu.be/Fygi3mQY0Ag
ודוגמאות לגרף בועות בתוכנת Excel:
https://youtu.be/Q1uiytD86OQ

תרשים קופסה ("BoxPlot"), שנקרא גם תרשים תיבה, נותן סיכום חזותי של התפלגות נתונים בעזרת תיבה וקווים תוחמים מחוץ לתיבה, המכונים "שפמים".
תרשים הקופסה מספק 5 דברים על קבוצת הנתונים: המינימום, הרבעון התחתון, החציון, הרבעון העליון והמקסימום.
בתרשים מוצגים בצורה מרוכזת הערכים המרכזיים והפיזור של הנתונים:
#הרבעון התחתון והעליון - אלה גבולות התיבה שהם לרוב הרבעון התחתון והעליון. אלו ערכים שמתחת להם נמצאים 25% ו-75% מהנתונים.
חציון - הקו שבתוך התיבה. זהו החציון (Median), הערך האמצעי של הנתונים.
ערכי המינימום והמקסימום - ערכים שקל לזהות, כי הם מוצגים על ידי קצוות הקווים היוצאים מהקופסה ומכונים "שפמים" (whiskers). השפמים מיקומם בגבול הערכים הקיצוניים, שהם המינימום והמקסימום. ואגב, באנגלית קוראים לתרשימי קופסה גם "תרשימי קופסה ושפמים" (box and whisker plots).
נקודות בודדות מחוץ לטווח השפמים מסמנות ערכים חריגים. כלומר נתונים יוצאי דופן גבוהים או נמוכים במיוחד.
לדוגמה, בתרשים הקופסה יכולים להיות מוצגים ציוני מבחן של שתי כיתות: עבור כל כיתה יש "תיבה" אחת. ניתן לראות מצב בו בכיתה A החציון קצת גבוה מ-70, בעוד בכיתה B החציון הוא סביב 72. פיזור הציונים בכיתה B יכול להיות גדול יותר (התיבה ארוכה יותר וכך גם שפמי כיתה B הארוכים יותר - מה שמראה שהציונים בה מפוזרים על פני טווח רחב יותר). יכולה להיות גם נקודת עיגול מתחת לכיתה B, שמשמעותה היא למשל תלמיד שקיבל ציון חריג נמוך במיוחד לעומת שאר תלמידי כיתתו.
#יתרונות
תרשים קופסה מאפשר השוואה מהירה בין התפלגויות של קבוצות שונות. בגרף אחד אפשר לשים מספר "תיבות" זו ליד זו (כמו בדוגמת שתי הכיתות) ולהבין מיד באיזו קבוצה הערכים באופן כללי גבוהים יותר, איפה הפיזור רחב או צר יותר והאם יש חריגים.
זהו מידע שיהיה קשה לראות בגרפים פשוטים כמו גרף עמודות (שמציגים רק ממוצע או סכום ולא את פיזור הנתונים).
בנוסף, התרשים מספק הרבה מידע במבט מרוכז אחד: ממוצע או חציון, טווח בין-רבעוני (הקופסה), טווח כללי (השפמים) וחריגים, מבלי שנצטרך לראות כל נקודה ונקודה בנפרד.
#התאמה
תרשים הקופסה מתאים במיוחד עבור נתונים כמותיים, כאשר חשוב להבין את הפיזור והמגמה המרכזית שלהם, במיוחד בהשוואה בין כמה קבוצות.
למשל, בציוני מבחן של כמה כיתות שונות, בגבהים של זכרים מול נקבות או בהתפלגות הכנסות בערים שונות - בכל אלו מעניין לא רק מה הממוצע אלא איך הנתונים נפרשים סביבו.
תרשים קופסה שימושי גם בזיהוי ערכים חריגים שיכולים להיות חשובים. כמו, למשל, זיהוי ניסוי מדעי ש"תפס כיוון שונה" משאר התוצאות כי הוא חריג.
#דוגמאות
דוגמה מהחיים: דמיינו בית חולים שמשווה את זמן ההמתנה בחדר המיון בשלושה סניפים שונים. באמצעות תרשים קופסה, יוצג כל סניף בתיבה. אפשר לראות באיזה בית חולים זמן ההמתנה החציוני (חציון) קצר ביותר ובאיזה הפיזור גדול.
ייתכן שבבית חולים אחד לרוב ממתינים 10-20 דקות (תיבה קטנה), בעוד שבאחר הזמנים מגוונים ונפרשים מ-5 דקות ועד שעה (תיבה ושפמים גדולים יותר). מידע כזה עוזר לזהות איפה השירות עקבי ומהיר יותר.
עוד תרשים לדוגמה יכול להיות באמצעות Box Plot של ציוני שתי כיתות (כיתה A וכיתה B). הקו האדום בכל תיבה הוא החציון, הקופסה מראה את טווח הציונים האמצעי, והנקודות (כמו עיגול לבן) הן ערכים חריגים.
הנה הסבר של תרשים הקופסה:
https://youtu.be/Ck5HMTnvfw0
דוגמה שימושית לתרשים כזה:
https://youtu.be/b2C9I8HuCe4
חמשת הנקודות העיקריות בתרשים הקופסה:
https://youtu.be/E7ewAxluyt0
הנתונים שמראה תרשים קופסה:
https://youtu.be/EVm1NhGod1w
כך תקראו תרשים קופסה:
https://youtu.be/fHLhBnmwUM0
ותרשים קופסה בתוכנת אקסל:
https://youtu.be/f7rkB7c-zDw
קשרים

מפת חום (Heatmap) מציגה טבלה של ערכים בשני ממדים כאשר הערכים מיוצגים כצבעים.
כלומר, יש לנו ציר אופקי וציר אנכי (למשל, ימים ושעות, או פריטים שונים מול תכונות שונות), ובנקודת המפגש של כל שני פרמטרים יש ערך מספרי שמיוצג על ידי צבע.
במפת חום לרוב משתמשים בסקאלה צבעונית. למשל, מכחול דרך צהוב עד אדום, כדי לציין מערך ערכים נמוכים עד גבוהים.
היתרון הוא שבמבט אחד ניתן לאתר דפוסים: אזורים חמים (בצבע בולט כמו אדום) לעומת קרים (כחול או צבע כהה) שמראים איפה הערכים גבוהים או נמוכים במיוחד.
לדוגמה, דמיינו heatmap שבו ניתן לראות את עומס המבקרים בחנות לאורך הימים והשעות. כל שורה מייצגת יום בשבוע וכל עמודה שעה ביום. בעוד הצבע הלבן-צהוב מצביע על שעות שיא עם הרבה לקוחות (צהרי היום ובערב), השחור-אדמדם מצביע על שעות שקטות (למשל באמצע הלילה או מוקדם בבוקר).
כך ניתן לראות במבט מהיר שבסופי שבוע (שבת-ראשון) בצהריים יש צבע בהיר מאוד, כלומר החנות עמוסה אז במיוחד.
#יתרונות
מפת חום מצטיינת ביכולת להראות הרבה מידע בתמונה אחת באופן אינטואיטיבי. היא טובה בזיהוי תבניות, כי העין שלנו מיד נמשכת לאזורים בולטים בצבעם. למשל, אם נשתמש במפת חום להצגת ציוני תלמידים במקצועות שונים (שורות תלמידים, עמודות מקצועות, וצבע = ציון), נוכל מיד להבחין באילו מקצועות כיתה שלמה חזקה (מה שייראה בצורת עמודה בולטת בצבע מסוים) או האם תלמיד ספציפי בולט לרעה או לטובה (שורה מסוימת עם צבעים קיצוניים).
#התאמה
מפת החום מתאימה במיוחד עבור נתונים בעלי שני ממדים של קטגוריות או רצף, כשעבור כל צירוף שלהם יש ערך מספרי.
זה יכול להיות זמנים מול מקומות (כמו בדוגמת החנות: לכל יום ושעה יש מספר של לקוחות), או אנשים מול תכונות (למשל, טבלת תלמידים וציוניהם בכמה מקצועות), או אפילו מטריצה של מתאם בין משתנים (כשרוצים לראות אילו משתנים קשורים, עם ערכים גבוהים בצבע בולט).
מפת חום שימושית גם למדעני נתונים בתחומים כמו ביולוגיה ובינה מלאכותית, כדי להציג מטריצות גדולות בצורה שקל לקלוט (כמו "DNA Microarray" בביולוגיה, שמציג ביטויי גנים שונים כדוגמאות צבע).
#דוגמאות
דוגמה מהחיים: רשת חברתית יכולה להציג למנהלי הקהילה מפה צבעונית של פעילות המשתמשים לפי שעה ויום: למשל, הצבעים יראו שבשעות הערב של סוף השבוע הפעילות באתר בשיאה (צבע חם מאוד) ואילו בשעות בוקר של אמצע השבוע הפעילות נמוכה (צבע קר).
דוגמה נוספת: אפליקציית תחבורה ציבורית עשויה להראות Heatmap של עומס נוסעים בתחנות שונות לאורך היום. כך ניתן לראות באילו תחנות ושעות יש עומס גדול (אדום), מה שעוזר בהקצאת משאבים כמו אוטובוסים נוספים בזמן הנכון.
מהי מפת חום?
https://youtu.be/Q3XFj3zJBuE
מפת חום בגוגל Sheet:
https://youtu.be/RuvbI3QcsFo
ליצור מפת חום בתוכנת אקסל:
https://youtu.be/4Ftu8ay4UKc
הרצאונת על מהי מפת חום ואיך להשתמש בה:
https://youtu.be/stgf2CfiXr4
ומפת חום מורכבת במיוחד:
https://youtu.be/NFbiSX6PYXo

גרף עמודות (Bar Chart) הוא גרף השוואתי, עם ציר אחד בלבד, המציג השוואה בין קטגוריות שונות בעזרת מלבנים או עמודות שכל אחד מהם מייצג קטגוריה.
גובה כל עמודה (או אורך, אם העמודות אופקיות) מראה לנו כמה גדול הערך של אותה קטגוריה, למשל שכיחות של משהו, כמה ממנו יש. למשל, גרף של מספר תושבים בערים שונות יראה לנו עמודות שונות, שכל אחת מהן מציגה את גודל האוכלוסיה בעיר המסוימת, את שכיחות התושבים בה.
ערך גבוה מיוצג על-ידי עמודה גבוהה וערך נמוך על-ידי עמודה נמוכה. כלומר הגרף מסוג זה הוא פשוט לקריאה: ניתן מיד לראות בו בעמודות מי בין הקטגוריות היא "הכי גדולה" ומי "הכי קטנה", מי יותר ומי פחות.
לדוגמה, אפשר להשתמש בגרף עמודות כדי להציג את מספר התלמידים בכל כיתה בשכבה, כאשר לכל כיתה יש עמודה בגובה המתאים למספר התלמידים בה.
#יתרונות
גרף עמודות מצטיין בהשוואת גדלים בין פריטים או קבוצות שונות בצורה ישירה. בניגוד לגרף עוגה, שבו קשה להשוות בדיוק גדלים של פרוסות, כאן אפשר לראות בבירור ובמדויק איזו עמודה גבוהה יותר, גם אם ההפרשים לעתים זעירים.
גרף העמודות עדיף לעיתים גם על גרף קו, כשהנתונים אינם רציפים אלא מחולקים לקטגוריות נפרדות (למשל סוגי מוצרים, ערים, קבוצות גיל וכדומה).
#מתי?
גרף העמודות מתאים במיוחד עבור נתונים קטגוריים - כלומר נתונים המחולקים לקבוצות או לסוגים ברורים. גרף כזה מתאים להראות כמויות, סכומים או מספר פריטים בכל קטגוריה.
הגרף יעיל גם להצגת נתונים של תקופות (חודשים, שנים) כשרוצים להשוות תקופה לתקופה ולא בהכרח להראות מגמה רציפה.
#דוגמאות
למשל, השוואת כמות הגשמים בחודשי השנה באמצעות עמודות, כשלכל חודש עמודה המציגה את כמות המשקעים בו.
דוגמה נוספת: גרף עמודות יכול להראות כמה משתמשים יש לכל רשת חברתית (פייסבוק, אינסטגרם, טוויטר וכו'), כאשר כל רשת מיוצגת בעמודה. כך רואים איזו רשת היא בעלת מספר המשתמשים הגדול ביותר בצורה ברורה.
הנה גרף עמודות:
https://youtu.be/WTVdncVCvKo
גרף עמודות המציג מספר ערכים השוואתיים מטבלת שכיחות (עברית):
https://youtu.be/ZrBw7vTRsUs
דוגמה לגרף עמודות אופקי:
https://youtu.be/wlEQ6h9ilUU
ותבנית לילדים ליצירת דיאגרמת עמודות, גרף עמודות (עברית):
https://youtu.be/RjYKvcvlies

היסטוגרמה (Histogram) דומה במראה לגרף עמודות, אך היא משרתת מטרה שונה: היא מראה התפלגות של נתונים רציפים. ציר אחד (בדרך כלל אופקי) מחולק ל"טווחים" או "אשכולות" של ערכים (בין X ל-Y, Y ל-Z, וכו') והציר האחר מראה כמה נתונים נופלים בכל טווח כזה.
כל עמודה בהיסטוגרמה מייצגת את מספר המקרים או התצפיות שהתגלו בטווח ערכים מסוים. כך למעשה ההיסטוגרמה נותנת מושג על צורת ההתפלגות – האם רוב הנתונים מרוכזים בטווח צר, פזורים באופן אחיד, או אולי יש שני "שיאים" וכו'.
אם נאסוף, לדוגמה, את ציוני המבחן של 100 תלמידים, נוכל ליצור היסטוגרמה שבה כל עמודה מראה כמה תלמידים קיבלו ציון בטווח מסוים (נגיד 50-60, 60-70, 70-80, וכו'). כך אפשר לראות האם רוב הכיתה קיבלה ציונים גבוהים, נמוכים, או שהתפלגו באופן שווה.
#יתרונות
היסטוגרמה מצטיינת בהצגת התפלגות ערכים – משהו שגרף עמודות רגיל אינו עושה, כי גרף עמודות מציג כל קטגוריה בנפרד ולא טווח רציף.
בעזרת היסטוגרמה אפשר לזהות במהירות מאפיינים של הנתונים כמו שכיחות (כמה פעמים ערכים מופיעים בטווח מסוים), האם יש הטיה לכיוון גבוה או נמוך והאם הנתונים מרוכזים סביב ערך מרכזי או מפוזרים.
כך, למשל, אפשר לראות אם יש "זנב ארוך" – כלומר מעט ערכים רחוקים מהמרכז (מה שיראה כעמודה בודדת רחוקה מהשאר).
#התאמה
היסטוגרמה מתאימה במיוחד עבור נתונים מספריים רציפים בכמות גדולה, כאשר רוצים להבין את הצורה הכללית שלהם.
כל מצב שבו יש מדידה כמותית להרבה פרטים - ציוני תלמידים, גבהים של אנשים, משך זמן שלוקח לאנשים לבצע משימה, טמפרטורות יומיות בחודש – יתאים להיסטוגרמה.
מה שכן, חשוב שלנתונים יהיה טווח ערכים רחב מספיק כדי לחלק לטווחים (Bins) ולהפיק תובנות מצורת ההצטברות שלהם.
#דוגמאות
דוגמה מהחיים היא של מורה שיכול להכין היסטוגרמה של ציוני הבחינה בכיתה כדי לראות את פיזור הציונים. הציר האופקי הוא טווחי ציונים, בעוד הציר האנכי הוא מספר התלמידים בכל טווח. כך ניתן לבחון האם יש שתי פסגות (האם למשל קבוצה גדולה קיבלה ציונים נמוכים וקבוצה גדולה אחרת ציונים גבוהים) או שהציונים מרוכזים סביב ציון ביניים.
דוגמה נוספת: היסטוגרמה של גילאי תושבי עיר – ציר אופקי טווחי גיל (0-9, 10-19, 20-29 וכו') והציר האנכי מספר התושבים בכל טווח. כך העירייה יכולה לראות אם יש הרבה צעירים, הרבה מבוגרים וכו', דברים שיכולים להשפיע על תכנון וסוג השירותים לתושבים.
מהי היסטוגרמה, מתי להשתמש בה ואיך?
https://youtu.be/haJyaQObNwU
היסטוגרמה בעולם ההשקעות:
https://youtu.be/Xv8gh2exXeE
מה ההבדל בין היסטוריה לגרף עמודות?
https://youtu.be/JsEwJD1mYpU
היסטוגרמה? - מתי להשתמש באיזה גרף?
https://youtu.be/yrTB5JSQPqY
כך תבנו היסטוגרמה:
https://youtu.be/fHX7myclXyk

בנהיגה בכלי רכב יבשתיים, כמו אופניים או מכונית, המהירות נמדדת בקילומטרים או במיילים לשעה. אבל כל מי שהתנסה או קרא על שיט באוניה או ביכטה, שמע ודאי את המונח קֶשֶר (Knot), או קשר ימי, המשמש למדידת המהירות בים.
לרשות ספנים בספינות עתיקות לא היו אמצעים כמו מפות מודרניות או מתקני ניווט מבוססי GPS. הם נזקקו לשיטה שתסייע להם לזהות את כיוון השיט הרצוי וכמה זמן עליהם לשוט עד שיגיעו לשם. מדידת מהירות הנסיעה של ספינה הייתה הכרחית כי ללא כלי שיאפשר אותה עלולים היו צוותי הספינות הללו להתרחק מהמסלול ולאבד את חייהם. מדידת המהירות של הספינה היה הכרחי כדי לנווט ולדעת מתי היא תגיע אל היעד.
המילה קשר מזכירה קשר בחבל ולמעשה זה העניין. כי הקֶשֶר הימי, הוא יחידת המדידה של המהירות הימית והיא קרויה על שם השיטה הקדומה למדידת מהירות של אוניות.
במאה ה-17, לפני מאות שנים, העלו ספנים אלמונים, בעלי יוזמה וכושר המצאה, רעיון למדידת המהירות. הם לקחו חבלים ארוכים וקשרו בהם קשרים, במרווחים מדויקים של 14.4 מטר. את החבלים הם שילבו במכשיר פשוט ביותר, שממנו יצאה חתיכת החבל עם הקשרים ובקצה שלה היא חוברה למשקולת עץ בצורת טריז. את טריז העץ המחובר לחבל השליכו אל המים, כשקצהו השני של החבל, זה עם המכשיר, נשאר מחובר לספינה.
וכך, תוך כדי שיט, שחררו המלחים את החבלים הללו. הם השתמשו בשעון חול למדידת פרק זמן קבוע, מה שנקרא "טיימר" (Timer). וכך ספרו המלחים כמה קשרים עברו באצבעותיהם בפרק הזמן המוקצב לשעון החול להשלים ירידה של כל החול. כך נהגו אז להכפיל את מספר הקשרים בשעה ולקבל את המהירות ב"קשר ימי".
כך נהגו הספנים כל הזמן לחשב את מהירות האוניה ונעשה חישוב של הממוצע שיאמר כמה מהר היא שטה. משידעו את מהירות הספינה הם חישבו בכל יום את המיקום שלהם בים וכמה זמן נותר להם עד שיגיעו ליעד שאליו הם מתכוונים להגיע.
כיום יש אמצעים חדשניים ומדויקים במיוחד למדידת מהירות הספינה. ספנים משתמשים ב-GPS, המבוסס על מדידת מיקום סופר מדויקת, שמתבצעת בעזרת רשת לוויינים וחיישני אולטרה סאונד. ועדיין, משתמשים גם היום במושג קילומטר הימי וגם בעולם התעופה. גם מטוסים מודדים את מהירותם בקשרים ובמיילים ימיים המבוססים על היקף כדור הארץ.
מדהים שכך הוליד מכשיר פשוט וחכם, שהומצא במאה ה-17, את המושגים המקובלים עד היום למדידת מהירות שיט ואף טיסה. קשר היא יחידה ששווה ל-1 מייל ימי לשעה. בקילומטרים היא בערך 1.852 קילומטר לשעה. קילומטר ימי מבוסס למעשה על היקף כדור הארץ. הוא שווה בדיוק לדקה של קו רוחב.
הנה מדידה של מהירות ומרחק הספינה באמצעות קשר:
http://youtu.be/LZY3FJGG_gQ?t=22s
והסבר על מדידת המהירות באמצעות קשרים בחבל:
https://youtu.be/RtvfYJFhYEg

גְּרָף (Graph Data), או גרף נתונים, הוא תיאור שבדרך כלל הוא דו-ממדי של מספר פרטי מידע המקושרים ביניהם על ידי יחסים כלשהם.
הגרף ישמש בדרך כלל להצגה חזותית של מידע כמותי. הוא מאפשר השוואה של הפריטים השונים זה לזה, בעזרת יחידות המידה שבדרך כלל מוצגות על הציר או על שני צירי הגרף. כי גם אם גרפים עתירי נתונים יוצגו לעתים עם מערכת צירים תלת-ממדית, בדרך כלל הם יוצגו בגרפים המבוססים על מערכת צירים דו-ממדית.
הציר האופקי, הציר שממש כמו האופק שאליו אנו מביטים נמתח לרוחב, יציג בדרך כלל את המשתנה. אם למשל נציג גרף של פופולריות של מוצר לאורך תקופה מסוימת, אז הציר האופקי יציג את הזמן, למשל את החודשים בשנה האחרונה.
הציר האנכי, העומד, יציג את הפונקציה. למשל בגרף של פופולריות המוצר בשנה האחרונה הציר הזה יציג את הפופולריות שלו, הפונקציה של המשתנה - כמה המוצר נמכר, או מה אחוז הנשאלים שאהבו את המוצר בסקר החודשי.
#למה צריך את זה?
גדולתו של הגרף היא בייצוג ויזואלי והשוואתי, באופן מופשט וללא מידע מיותר. כל זה לגבי קבוצת הפריטים או הנתונים, כשכולם מקושרים ביניהם באופן כלשהו.
יתרונם הגדול של הגרפים הוא בקלות ובמהירות של קליטת המידע מהם. גרף טוב יאפשר זיהוי מהיר של הקשר בין הנתונים והיחסים ביניהם, לעתים גם כולל המגמות שניתן לזהות בהם והחריגות שבין הנתונים.
#סוגי גרפים
ישנם כמה סוגי גרפים, כשלכל סוג יש יתרונות משלו ושימושים מתאימים לסוג המידע שהוא מציג היטב לצרכי ויזואליזציה של נתונים.
הגרפים הבולטים, השכיחים והשימושיים ביותר הם גרף עמודות, גרף קו, גרף עוגה, היסטוגרמה, גרף פיזור, תרשים קופסה (Box Plot), גרף בועות, גרף רציף, גרף נרות יפניים (גרף קו המציג את המדידות בניתוח טכני באופן משוכלל יותר מנקודות על הקו) ומפת חום (Heatmap) שהיא מעט שונה אבל נחשבת גם היא לסוג של גרף.
למחקר תאורטי נרחב זכו הגרפים במסגרת תורת הגרפים. ישנם סוגי גרפים שונים. להיכרות איתם ראו את תגית "סוגי גרפים".
הנה הסבר לילדים על מה זה גרף:
https://youtu.be/LW7I0Skjaew
כמה מסוגי הגרפים שמשתמשים בהם:
https://youtu.be/bmY28wdGL9M
איך יודעים באיזה גרף להשתמש בכל הקשר?
https://youtu.be/o7F-tbBl_hA
גרף נתונים בקו שמדגים את השינויים לאורך זמן (עברית):
https://youtu.be/siBhC7scAdQ
כך אפשר לזהות הטעיה באמצעות גרף (מתורגם):
https://youtu.be/E91bGT9BjYk
וגרף הנרות היפניים בעולם המסחר במניות (עברית):
https://youtu.be/FPZbtNtbMtc?long=yes
למה משמש גרף פיזור?
גרף פיזור (Scatter Plot) הוא סוג של גרף המציג נקודות בודדות במערכת צירים, כשכל נקודה מייצגת תצפית אחת עם שני ערכים: אחד לערך הציר האופקי (X) ואחד לערך הציר האנכי (Y). בדרך זו ניתן לראות קשר אפשרי בין שני משתנים – האם יש ביניהם מגמה משותפת, קוֹרֵלַצְיָה, קשר כלשהו - או שהם בלתי תלויים.
הנקודות מפוזרות במישור בהתאם לערכיהן. אם למשל הערכים נוטים לעלות יחד (כש-X גדול גם Y גדול), נראה שהנקודות מתגבשות בקו אלכסוני עולה. לעומת זאת, אם אין קשר, הן תהיינה מפוזרות בצורה עננית וללא כיוון ברור.
לדוגמה, נוכל לצייר גרף פיזור שבו כל נקודה היא תלמיד: המיקום האופקי הוא מספר שעות הלמידה שלו למבחן, והמיקום האנכי הוא הציון שקיבל. אם נראה שהנקודות יוצרות נטייה אלכסונית (ככל שלמדו יותר שעות הציונים שלהם עולים), נסיק מכך שיש קשר חיובי בין זמן הלימוד לציון.
לחילופין, אם המצב הוא שהנקודות פזורות ללא סדר, כשחלק שלמדו מעט קיבלו ציון גבוה ואחרים שלמדו הרבה קיבלו ציון נמוך, נבין מכך שאין קשר ברור.
#יתרונות
גרף פיזור מצטיין בהמחשת קשרים ותבניות בין שני משתנים כמותיים. בשונה מגרפים כמו עמודות או קו, כאן כל פרט מופיע בנפרד כנקודה, וכך רואים גם את הפיזור וגם את צברי נקודות, ריכוזים של נקודות.
יתרון נוסף של גרף הפיזור הוא באפשרות לזהות בקלות ערכים חריגים (outliers), כנקודות שרחוקות מכל השאר.
#התאמה
גרף פיזור מתאים במיוחד עבור בדיקת קוֹרֵלַצְיָה (בעברית מִתְאָם), קשר או תלות בין שני דברים שנמדדים באופן מספרי.
דוגמאות? - מה הקשר בין משקל לגובה של אנשים? או בין כמות שעות צפייה בטלוויזיה לציונים בבית הספר?
כלומר גרף פיזור יהיה הבחירה הטבעית לכל זוג של נתונים מספריים שחשוב לנו לדעת אם יש ביניהם קשר. לעיתים גם מוסיפים קו מגמה או מחשבים מִתאם, קורלציה (correlation) כדי לכמת את הקשר, אבל ויזואלית הגרף כבר נותן תחושה טובה של זה.
#דוגמאות
קבלו דוגמה מהחיים - חוקרת עשויה להשתמש בגרף פיזור כדי לבדוק את הקשר בין כמות הפעילות הגופנית השבועית של אנשים לבין לחץ הדם שלהם. כל אדם מיוצג בנקודה אית, כשציר ה-X הוא שעות הספורט בשבוע, בעוד ציר Y הוא רמת לחץ הדם. אם מתגלה שיותר ספורט נוטה להתאים ללחץ דם נמוך יותר (נקודות לכיוון אלכסון יורד), זה רמז לקשר שלילי בין המשתתנים (יותר פעילות, פחות לחץ דם).
דוגמה נוספת: גרף פיזור של גודל דירה (במ"ר) מול גובה שכר הדירה. אם אכן קיים קשר כזה בשוק הדיור, הרי שנקודות ערוכות בעלייה יראו שדירות גדולות יותר נוטות גם לעלות יותר.
הנה גרף פיזור:
https://youtu.be/1ZAxR2KgM0g
כך יוצרים גרף פיזור באקסל:
https://youtu.be/P4T41HT4Be8
כך קוראים אותו:
https://youtu.be/Qsges3fJVGM
גרף פיזור מצוין לקורלציות:
https://youtu.be/AxyDalIvKIA
וכך נבין את גרף הפיזור:
https://youtu.be/hKNFn2E2biw
גרף פיזור (Scatter Plot) הוא סוג של גרף המציג נקודות בודדות במערכת צירים, כשכל נקודה מייצגת תצפית אחת עם שני ערכים: אחד לערך הציר האופקי (X) ואחד לערך הציר האנכי (Y). בדרך זו ניתן לראות קשר אפשרי בין שני משתנים – האם יש ביניהם מגמה משותפת, קוֹרֵלַצְיָה, קשר כלשהו - או שהם בלתי תלויים.
הנקודות מפוזרות במישור בהתאם לערכיהן. אם למשל הערכים נוטים לעלות יחד (כש-X גדול גם Y גדול), נראה שהנקודות מתגבשות בקו אלכסוני עולה. לעומת זאת, אם אין קשר, הן תהיינה מפוזרות בצורה עננית וללא כיוון ברור.
לדוגמה, נוכל לצייר גרף פיזור שבו כל נקודה היא תלמיד: המיקום האופקי הוא מספר שעות הלמידה שלו למבחן, והמיקום האנכי הוא הציון שקיבל. אם נראה שהנקודות יוצרות נטייה אלכסונית (ככל שלמדו יותר שעות הציונים שלהם עולים), נסיק מכך שיש קשר חיובי בין זמן הלימוד לציון.
לחילופין, אם המצב הוא שהנקודות פזורות ללא סדר, כשחלק שלמדו מעט קיבלו ציון גבוה ואחרים שלמדו הרבה קיבלו ציון נמוך, נבין מכך שאין קשר ברור.
#יתרונות
גרף פיזור מצטיין בהמחשת קשרים ותבניות בין שני משתנים כמותיים. בשונה מגרפים כמו עמודות או קו, כאן כל פרט מופיע בנפרד כנקודה, וכך רואים גם את הפיזור וגם את צברי נקודות, ריכוזים של נקודות.
יתרון נוסף של גרף הפיזור הוא באפשרות לזהות בקלות ערכים חריגים (outliers), כנקודות שרחוקות מכל השאר.
#התאמה
גרף פיזור מתאים במיוחד עבור בדיקת קוֹרֵלַצְיָה (בעברית מִתְאָם), קשר או תלות בין שני דברים שנמדדים באופן מספרי.
דוגמאות? - מה הקשר בין משקל לגובה של אנשים? או בין כמות שעות צפייה בטלוויזיה לציונים בבית הספר?
כלומר גרף פיזור יהיה הבחירה הטבעית לכל זוג של נתונים מספריים שחשוב לנו לדעת אם יש ביניהם קשר. לעיתים גם מוסיפים קו מגמה או מחשבים מִתאם, קורלציה (correlation) כדי לכמת את הקשר, אבל ויזואלית הגרף כבר נותן תחושה טובה של זה.
#דוגמאות
קבלו דוגמה מהחיים - חוקרת עשויה להשתמש בגרף פיזור כדי לבדוק את הקשר בין כמות הפעילות הגופנית השבועית של אנשים לבין לחץ הדם שלהם. כל אדם מיוצג בנקודה אית, כשציר ה-X הוא שעות הספורט בשבוע, בעוד ציר Y הוא רמת לחץ הדם. אם מתגלה שיותר ספורט נוטה להתאים ללחץ דם נמוך יותר (נקודות לכיוון אלכסון יורד), זה רמז לקשר שלילי בין המשתתנים (יותר פעילות, פחות לחץ דם).
דוגמה נוספת: גרף פיזור של גודל דירה (במ"ר) מול גובה שכר הדירה. אם אכן קיים קשר כזה בשוק הדיור, הרי שנקודות ערוכות בעלייה יראו שדירות גדולות יותר נוטות גם לעלות יותר.
הנה גרף פיזור:
https://youtu.be/1ZAxR2KgM0g
כך יוצרים גרף פיזור באקסל:
https://youtu.be/P4T41HT4Be8
כך קוראים אותו:
https://youtu.be/Qsges3fJVGM
גרף פיזור מצוין לקורלציות:
https://youtu.be/AxyDalIvKIA
וכך נבין את גרף הפיזור:
https://youtu.be/hKNFn2E2biw
מהו גרף עוגה ומה הוא מציג היטב?
גרף עוגה (Pie Chart), או דיאגרמת עוגה, הוא גרף נתונים ללא צירים המציג בפלחים צבעוניים את החלקים מתוך שלם.
יתרונו הוא בהצגת ההתפלגות של השלם לחלקים היחסיים, כמו גם של היחס שבין החלקים השונים ובין כל אחד מהם לבין השלם.
גרף עוגה נקרא כך כי צורתו כעין עוגה עגולה המחולקת לפרוסות. כל פרוסה מייצגת קטגוריה או חלק מסוים מתוך ה"עוגה" השלמה, וגודל הפרוסה (הזווית או השטח שלה) מראה את היחס או האחוז של אותו חלק מתוך השלם.
כל הפרוסות שמציגות חלוקת שלם לחלקים יוצרות מעגל שלם ולמעשה 100% מהנתון. גרף עוגה מאפשר לראות בבת-אחת איזה חלק תופסת כל קטגוריה מתוך הסך הכולל. כך ניתן להציג בעזרת גרף עוגה למשל את חלוקת התקציב חודשי של משק הבית: פרוסה אחת עבור אחוז ההוצאה על מזון, פרוסה אחרת עבור דיור, פרטסה לתחבורה, לבידור וכו'. כך רואים באילו סעיפים היה שיעור ההוצאות הגדול ביותר.
#יתרונות
גרף עוגה נותן תמונה מהירה של יחס החלקים בתוך שלם אחד. בניגוד לגרף עמודות המשווה כמויות מוחלטות, גרף העוגה מתמקד בהמחשת ההרכב היחסי – מה הגודל היחסי של כל חלק. הוא יעיל במיוחד כשיש רק כמה חלקים גדולים וברורים ומאפשר לזהות מיד למשל מה "הפרוסה הגדולה ביותר", או החלקים הגדולים יותר בחלוקה.
#מתי משתמשים בו?
גרף העוגה מתאים במיוחד להצגת אחוזים או חלקים מתוך סך הכל של השלם. בכל מצב שבו הנתונים הם חלקי סך (כלומר, סך הכול 100% מחולק בין קטגוריות), גרף עוגה יכול להתאים.
למשל, פילוח אוכלוסייה לפי קבוצות גיל, באחוזים מתוך כלל האוכלוסייה. או בפילוח חלוקת הזמן של סטודנט ביומיום שלו, כלומר כמה אחוזים מהזמן מוקדשים לכל פעילות.
#דוגמאות
יש דוגמאות מהמדע, כמו גרף עוגה שיכול להראות את ההרכב של האוויר שאנו נושמים: כ-78% חנקן, 21% חמצן, וכ-1% גזים אחרים. כל גז מיוצג בפרוסת עוגה בגודל מתאים.
דוגמה יומיומית היא חלוקת שעות היממה של תלמיד תיכון. אם ה"עוגה" כוללת 24 שעות, היא מחולקת לפרוסות – שינה, לימודים בבית הספר, שיעורי בית, שעות פנאי וכדומה. כך מראים בגרף אחד כמה משעות היום מוקדשות לכל פעילות.
הסבר של גרף העוגה:
https://youtu.be/GjJdZaQrItg
מצגת וידאו:
https://youtu.be/18o0iqU8Ke4
מהו גרף העוגה?
https://youtu.be/P2HIgjqIGiU
גרף עוגה (Pie Chart), או דיאגרמת עוגה, הוא גרף נתונים ללא צירים המציג בפלחים צבעוניים את החלקים מתוך שלם.
יתרונו הוא בהצגת ההתפלגות של השלם לחלקים היחסיים, כמו גם של היחס שבין החלקים השונים ובין כל אחד מהם לבין השלם.
גרף עוגה נקרא כך כי צורתו כעין עוגה עגולה המחולקת לפרוסות. כל פרוסה מייצגת קטגוריה או חלק מסוים מתוך ה"עוגה" השלמה, וגודל הפרוסה (הזווית או השטח שלה) מראה את היחס או האחוז של אותו חלק מתוך השלם.
כל הפרוסות שמציגות חלוקת שלם לחלקים יוצרות מעגל שלם ולמעשה 100% מהנתון. גרף עוגה מאפשר לראות בבת-אחת איזה חלק תופסת כל קטגוריה מתוך הסך הכולל. כך ניתן להציג בעזרת גרף עוגה למשל את חלוקת התקציב חודשי של משק הבית: פרוסה אחת עבור אחוז ההוצאה על מזון, פרוסה אחרת עבור דיור, פרטסה לתחבורה, לבידור וכו'. כך רואים באילו סעיפים היה שיעור ההוצאות הגדול ביותר.
#יתרונות
גרף עוגה נותן תמונה מהירה של יחס החלקים בתוך שלם אחד. בניגוד לגרף עמודות המשווה כמויות מוחלטות, גרף העוגה מתמקד בהמחשת ההרכב היחסי – מה הגודל היחסי של כל חלק. הוא יעיל במיוחד כשיש רק כמה חלקים גדולים וברורים ומאפשר לזהות מיד למשל מה "הפרוסה הגדולה ביותר", או החלקים הגדולים יותר בחלוקה.
#מתי משתמשים בו?
גרף העוגה מתאים במיוחד להצגת אחוזים או חלקים מתוך סך הכל של השלם. בכל מצב שבו הנתונים הם חלקי סך (כלומר, סך הכול 100% מחולק בין קטגוריות), גרף עוגה יכול להתאים.
למשל, פילוח אוכלוסייה לפי קבוצות גיל, באחוזים מתוך כלל האוכלוסייה. או בפילוח חלוקת הזמן של סטודנט ביומיום שלו, כלומר כמה אחוזים מהזמן מוקדשים לכל פעילות.
#דוגמאות
יש דוגמאות מהמדע, כמו גרף עוגה שיכול להראות את ההרכב של האוויר שאנו נושמים: כ-78% חנקן, 21% חמצן, וכ-1% גזים אחרים. כל גז מיוצג בפרוסת עוגה בגודל מתאים.
דוגמה יומיומית היא חלוקת שעות היממה של תלמיד תיכון. אם ה"עוגה" כוללת 24 שעות, היא מחולקת לפרוסות – שינה, לימודים בבית הספר, שיעורי בית, שעות פנאי וכדומה. כך מראים בגרף אחד כמה משעות היום מוקדשות לכל פעילות.
הסבר של גרף העוגה:
https://youtu.be/GjJdZaQrItg
מצגת וידאו:
https://youtu.be/18o0iqU8Ke4
מהו גרף העוגה?
https://youtu.be/P2HIgjqIGiU
מהו גרף קו ובמה הוא מצטיין?
גרף קו (Line Chart) מציג נתונים נקודתיים המחוברים באמצעות קו רציף. ציר אחד (בדרך כלל הציר האופקי) מייצג את הזמן או סדרה רציפה אחרת והציר האנכי מייצג את הערך הנמדד. כל נקודה על הגרף מראה את הערך בנקודת זמן מסוימת, כשהקו המחבר בין הנקודות מראה את השינוי בין הערכים ברצף. בצורה זו הגרף מדגיש מגמה או טרנד – האם הערכים עולים, יורדים, או מתנודדים לאורך הציר הרציף. לדוגמה, נוכל לצייר גרף קו של טמפרטורות במשך השבוע: על הציר האופקי הימים ובציר האנכי הטמפרטורה בכל יום, והקו יראה אם נעשה חם יותר או קר יותר במהלך אותם ימים.
#יתרונות
גרף הקו מצטיין בהצגת מגמות ושינויים לאורך זמן. הוא מאפשר לראות בצורה חלקה אם הנתונים בעלייה, בירידה, או שישנן תנודות חוזרות. בהשוואה לגרף עמודות, גרף הקו נותן תחושה אינטואיטיבית יותר של "זרימת" הנתונים בזמן. למשל, אם רוצים לראות שינוי חודשי, קו מתמשך מקל לזהות שיאים ושפל בניגוד לעמודות שבהן צריך לדמיין קו מעליהן.
#התאמה
גרף קווי מתאים במיוחד עבור נתוני סדרה עוקבת או נתונים רציפים בזמן. כל מידע שמתפתח לאורך ציר מספרי רציף – לרוב ציר זמן (ימים, חודשים, שנים ואפילו דקות ושעות) – מתאים מאוד לגרף קו. הוא שימושי גם כשצריך להשוות כמה סדרות נתונים לאורך זמן על אותו גרף (למשל, טמפרטורה בעיר א' מול עיר ב' לאורך השנה, בעזרת שני קווים, לרוב בצבעים שונים).
#דוגמאות
דוגמה מהחיים: במעקב אחר קצב הלב במהלך פעילות ספורטיבית, אם הקו מטפס ויורד הוא מראה איך הדופק משתנה במשך האימון. דוגמה נוספת ופשוטה: גרף קו של מספר הצופים בערוץ יוטיוב לאורך השנה - אם בתחילת השנה היו מעט צופים ובסופה הרבה, הקו יהיה במגמת עליה, ובמבט אחד נבחין בכך.
הנה גרף קו:
https://youtu.be/n2YkbdNORp8
כך נצייר גרף קו שמציג שינוי של נתונים לאורך זמן (שני קווים בשני צבעים):
https://youtu.be/a8LN-v3MyDg
כך מכינים גרף קו בתוכנת Canva:
https://youtu.be/YO7mwE8rdyQ
ההבדל בין גרף קו לגרף עמודות:
https://youtu.be/-9QdQCdE9nc
וכך מכינים את גרף הקו בגיליון Excel (עברית):
https://youtu.be/A8AtpGqb2w4
גרף קו (Line Chart) מציג נתונים נקודתיים המחוברים באמצעות קו רציף. ציר אחד (בדרך כלל הציר האופקי) מייצג את הזמן או סדרה רציפה אחרת והציר האנכי מייצג את הערך הנמדד. כל נקודה על הגרף מראה את הערך בנקודת זמן מסוימת, כשהקו המחבר בין הנקודות מראה את השינוי בין הערכים ברצף. בצורה זו הגרף מדגיש מגמה או טרנד – האם הערכים עולים, יורדים, או מתנודדים לאורך הציר הרציף. לדוגמה, נוכל לצייר גרף קו של טמפרטורות במשך השבוע: על הציר האופקי הימים ובציר האנכי הטמפרטורה בכל יום, והקו יראה אם נעשה חם יותר או קר יותר במהלך אותם ימים.
#יתרונות
גרף הקו מצטיין בהצגת מגמות ושינויים לאורך זמן. הוא מאפשר לראות בצורה חלקה אם הנתונים בעלייה, בירידה, או שישנן תנודות חוזרות. בהשוואה לגרף עמודות, גרף הקו נותן תחושה אינטואיטיבית יותר של "זרימת" הנתונים בזמן. למשל, אם רוצים לראות שינוי חודשי, קו מתמשך מקל לזהות שיאים ושפל בניגוד לעמודות שבהן צריך לדמיין קו מעליהן.
#התאמה
גרף קווי מתאים במיוחד עבור נתוני סדרה עוקבת או נתונים רציפים בזמן. כל מידע שמתפתח לאורך ציר מספרי רציף – לרוב ציר זמן (ימים, חודשים, שנים ואפילו דקות ושעות) – מתאים מאוד לגרף קו. הוא שימושי גם כשצריך להשוות כמה סדרות נתונים לאורך זמן על אותו גרף (למשל, טמפרטורה בעיר א' מול עיר ב' לאורך השנה, בעזרת שני קווים, לרוב בצבעים שונים).
#דוגמאות
דוגמה מהחיים: במעקב אחר קצב הלב במהלך פעילות ספורטיבית, אם הקו מטפס ויורד הוא מראה איך הדופק משתנה במשך האימון. דוגמה נוספת ופשוטה: גרף קו של מספר הצופים בערוץ יוטיוב לאורך השנה - אם בתחילת השנה היו מעט צופים ובסופה הרבה, הקו יהיה במגמת עליה, ובמבט אחד נבחין בכך.
הנה גרף קו:
https://youtu.be/n2YkbdNORp8
כך נצייר גרף קו שמציג שינוי של נתונים לאורך זמן (שני קווים בשני צבעים):
https://youtu.be/a8LN-v3MyDg
כך מכינים גרף קו בתוכנת Canva:
https://youtu.be/YO7mwE8rdyQ
ההבדל בין גרף קו לגרף עמודות:
https://youtu.be/-9QdQCdE9nc
וכך מכינים את גרף הקו בגיליון Excel (עברית):
https://youtu.be/A8AtpGqb2w4
מהי הלחנה אלגוריתמית?
הקשר בין מתמטיקה ומוסיקה ידוע מזה שנים רבות ונחקר לעומק, בניתוחים שכללו חקירה של המוסיקה של יוהאן סבסטיאן באך ומלחינים אחרים, שיצרו מוסיקה שיש לה תבניות מתמטיות מאורגנות ומסודרות להפליא, הן מבחינת התוצאה המוסיקלית והן בארגון ובסדר המתמטי המפתיעים שלהן.
תוכנה להלחנה אלגוריתמית (Algorithmic composition) היא תוכנה שמשתמשת באותו סדר ובאותן שיטות, כדי לסייע ליוצרים מוסיקליים בעידן הנוכחי לייצר מוסיקה מעניינת ומקורית, ביחד עם הטכנולוגיה הממוחשבת.
קומפוזיציה אלגוריתמית, או הלחנה אלגוריתמית, משתמשת באלגוריתמים, קבצי הוראות או מעין "מתכוני הלחנה", לצורך ההלחנה של מוסיקה. כל תוכנה להלחנה אלגוריתמית משלבת נוסחאות מתמטיות שמוזנות אליה, ביחד עם רמת אקראיות מסוימת שהיא מתוכנתת לייצר, כל אלה בכדי להלחין "מוסיקה אלגוריתמית".
בתוכנות או תכניות מחשב שנכתבו להלחנה אלגוריתמית נמצא מחולל אלגוריתמים, שמסוגל ליצור מבנים מוסיקליים מורכבים, המייצרים מוסיקה אלקטרונית. המוסיקאי המשתמש בכלי ממוחשב כזה, בין אם הוא תוכנה למחשב או שהוא שירות מקוון באינטרנט, בוחר אפשרויות שונות והגדרות מוסיקליות, שאותן התוכנה מעבדת בהלחנה אלגוריתמית ויוצרת את התוצרים המשלבים את ההחלטות שקיבל המוסיקאי, עם היכולות האקראיות והתבניתיות שיש למכונה. התוצאה היא מוסיקה.
תוכנות כאלה מצוידות ביכולות המצאה כמעט אינסופיות ויכולות להמציא מיליוני אפשרויות של לחנים ותבניות מוסיקליות שלא יחזרו על עצמן, מבחינת התוצר המוסיקלי שהן מנגנות, גם אם ינגנו ברציפות במשך שנים ארוכות!
הנה שיר על עולם ההלחנה האלגוריתמית שנכתב בעצמו על ידי פדריקו רובן ביחד עם "הלהקה האלגוריתמית" שלו - תוכנה:
https://youtu.be/H8BvvSRgS8c
הנה תוכנה שנכתבה לקומפוזיציה אלגוריתמית בסביבת הפיתוח Max:
https://youtu.be/Zx_y2muZfyg
ומוסיקה אלגוריתמית שנוצרה על ידי תוכנה:
https://youtu.be/6-GI0we1tBQ
הקשר בין מתמטיקה ומוסיקה ידוע מזה שנים רבות ונחקר לעומק, בניתוחים שכללו חקירה של המוסיקה של יוהאן סבסטיאן באך ומלחינים אחרים, שיצרו מוסיקה שיש לה תבניות מתמטיות מאורגנות ומסודרות להפליא, הן מבחינת התוצאה המוסיקלית והן בארגון ובסדר המתמטי המפתיעים שלהן.
תוכנה להלחנה אלגוריתמית (Algorithmic composition) היא תוכנה שמשתמשת באותו סדר ובאותן שיטות, כדי לסייע ליוצרים מוסיקליים בעידן הנוכחי לייצר מוסיקה מעניינת ומקורית, ביחד עם הטכנולוגיה הממוחשבת.
קומפוזיציה אלגוריתמית, או הלחנה אלגוריתמית, משתמשת באלגוריתמים, קבצי הוראות או מעין "מתכוני הלחנה", לצורך ההלחנה של מוסיקה. כל תוכנה להלחנה אלגוריתמית משלבת נוסחאות מתמטיות שמוזנות אליה, ביחד עם רמת אקראיות מסוימת שהיא מתוכנתת לייצר, כל אלה בכדי להלחין "מוסיקה אלגוריתמית".
בתוכנות או תכניות מחשב שנכתבו להלחנה אלגוריתמית נמצא מחולל אלגוריתמים, שמסוגל ליצור מבנים מוסיקליים מורכבים, המייצרים מוסיקה אלקטרונית. המוסיקאי המשתמש בכלי ממוחשב כזה, בין אם הוא תוכנה למחשב או שהוא שירות מקוון באינטרנט, בוחר אפשרויות שונות והגדרות מוסיקליות, שאותן התוכנה מעבדת בהלחנה אלגוריתמית ויוצרת את התוצרים המשלבים את ההחלטות שקיבל המוסיקאי, עם היכולות האקראיות והתבניתיות שיש למכונה. התוצאה היא מוסיקה.
תוכנות כאלה מצוידות ביכולות המצאה כמעט אינסופיות ויכולות להמציא מיליוני אפשרויות של לחנים ותבניות מוסיקליות שלא יחזרו על עצמן, מבחינת התוצר המוסיקלי שהן מנגנות, גם אם ינגנו ברציפות במשך שנים ארוכות!
הנה שיר על עולם ההלחנה האלגוריתמית שנכתב בעצמו על ידי פדריקו רובן ביחד עם "הלהקה האלגוריתמית" שלו - תוכנה:
https://youtu.be/H8BvvSRgS8c
הנה תוכנה שנכתבה לקומפוזיציה אלגוריתמית בסביבת הפיתוח Max:
https://youtu.be/Zx_y2muZfyg
ומוסיקה אלגוריתמית שנוצרה על ידי תוכנה:
https://youtu.be/6-GI0we1tBQ
מה זה טרק?
"טרק" (Trek) הוא טיול שעושים בהליכה, בטבע, בהרים וכן הלאה. הטרקים ברובם הם למקומות מרוחקים וקשים להגעה בדרך אחרת, כמו טיפוס על הרים והליכה למקומות קשים להגעה.
לרוב רואים במהלך ה"טרקים" דברים מופלאים ומיוחדים. זה כולל נופים מרהיבים, צמחים מיוחדים, בעלי חיים מגוונים ולא תמיד מוכרים, אנשים שחיים בצורות חיים מעניינות ותופעות טבע לא רגילות.
הטרק הוא גם שילוב של פעילות גופנית נהדרת ועל הדרך, תרתי משמע, חווים גם חוויות עם האנשים שאיתם מטיילים ויוצרים קשרים מיוחדים ולא פעם משני חיים, עם אנשים מכל העולם.
הנה סרטון שמציג טרק בהרים:
http://youtu.be/NzIDCJV1SeE
וטרק להרי הפמיר שבטג'יקיסטן:
http://youtu.be/th7sL4lyfcY
"טרק" (Trek) הוא טיול שעושים בהליכה, בטבע, בהרים וכן הלאה. הטרקים ברובם הם למקומות מרוחקים וקשים להגעה בדרך אחרת, כמו טיפוס על הרים והליכה למקומות קשים להגעה.
לרוב רואים במהלך ה"טרקים" דברים מופלאים ומיוחדים. זה כולל נופים מרהיבים, צמחים מיוחדים, בעלי חיים מגוונים ולא תמיד מוכרים, אנשים שחיים בצורות חיים מעניינות ותופעות טבע לא רגילות.
הטרק הוא גם שילוב של פעילות גופנית נהדרת ועל הדרך, תרתי משמע, חווים גם חוויות עם האנשים שאיתם מטיילים ויוצרים קשרים מיוחדים ולא פעם משני חיים, עם אנשים מכל העולם.
הנה סרטון שמציג טרק בהרים:
http://youtu.be/NzIDCJV1SeE
וטרק להרי הפמיר שבטג'יקיסטן:
http://youtu.be/th7sL4lyfcY
