שלום,
נראה שכבר הכרתם את אאוריקה. בטח כבר גיליתם כאן דברים מדהימים, אולי כבר שאלתם שאלות וקיבלתם תשובות טובות.
נשמח לראות משהו מכם בספר האורחים שלנו: איזו מילה טובה, חוות דעת, עצה חכמה לשיפור או כל מה שיש לכם לספר לנו על אאוריקה, כפי שאתם חווים אותה.
»
«
 מה לגבישים קריסטליים ולחתך הזהב?
מה לגבישים קריסטליים ולחתך הזהב?
תגליתו הגדולה של זוכה פרס נובל הישראלי דן שכטמן הם הגבישים הכמו-מחזוריים או בשפת הכימאים "קוואזי-גבישים" (quasicrystals) או "גביש קווזיפריודי".
הכל התחיל בבוקר אחד בחודש אפריל 1982. כשהביט במיקרוסקופ האלקטרוני שלו, ראה דן שכטמן סידור אטומים שהיה מנוגד לחלוטין לחוקי הטבע. הוא הרי למד תמיד שהאטומים שבגבישים מוצקים יוצרים תמיד תבניות סימטריות, שחוזרות על עצמן שוב ושוב, באופן מחזורי. התבניות שהוא ראה היו סדירות ותואמות את חוקי המתמטיקה, אך הן לא חזרו על עצמן אף פעם.
שכטמן גילה גביש כמו-מחזורי. בניגוד לגבישים רגילים, שהם בעלי סריג מחזורי, הגביש הכמו-מחזורי הוא בעל סימטריה בתבניות סדורות שלא חוזרות על עצמן אף פעם. בקוואזי-גבישים כאלו ראה שכטמן מעין פסיפסים שהזכירו לו את הפסיפסים והעיטורים שמקובלים באמנות הערבית מאז ימי הביניים, כאלה שניתן לראות במסגדים ובארמונות ערביים, מארמון אלהמברה שבדרום ספרד ועד ארמונות הפאר שבאיראן. אלא שבקוואזי-גביש הם משוכפלים פעם אחר פעם ברמת האטום!
כשפרסם שכטמן את ממצאיו טענו חוקרים ומומחים בתחום שהתצורה שגילה היא בלתי אפשרית ולא הגיונית. הכימאים התרגלו שהחזרה והמחזוריות הן חלק בלתי נפרד מהמבנה של הגביש וכאן בא המדען הישראלי וטוען שלא כך הדברים. הוא מצא את עצמו במוקד של מתקפה מדעית. במשך שנים רבות נאלץ להיאבק כנגד המומחים והידע המקובל בתחום המדעי. במהלך המאבק, שלא תמיד היה נעים, הוא מצא עצמו מגורש מקבוצת המחקר שלו. קביעותיו המדעיות נראו לרבים בעייתיות, אבל הוא עמד על שלו וסיפק הסברים וממצאים שהלכו וחיזקו את דעתו.
טיפין טיפין החלו הדעות משתנות. דן שכטמן אילץ את עולם הכימיה לשקול מחדש את התפיסה המקובלת בנוגע לטיבו הבסיסי של החומר. כשזכה בשנת 2011 בפרס נובל לכימיה על תגלית זו, הוא קיבל סוג של הכרה בכך שהוא ניצח במאבקו והצליח לשנות את הדעה המקובלת לגבי הכימיה של חומרים מוצקים.
כיום נמצאו הוכחות רבות לממצאיו של שכטמן. מדען אחד מצא את הגבישים הללו במינרלים שהוציא מנהר רוסי. מדענים אחרים יצרו גבישים קריסטליים כאלו באופן מלאכותי במעבדה. חוקרים אחרים מצאו שהקוואזי גבישים מחזקים את סוגי פלדה מסוימים והופכים אותה מחושלת וחזקה במיוחד. גם התעשייה כבר נערכת להשתמש בגבישים הללו לייצור של מכשירים חזקים מאי-פעם.
מדענים רבים מצאו בקוואזי-גבישים של שכטמן את "יחס הזהב", או בשמו הנוסף "חיתוך הזהב". היחס זה, שמאז יוון העתיקה השתמשו בו אדריכלים, אמנים ומהנדסים בתרבויות שונות ובהקשרים מגוונים, מופיע גם בגיאומטריה וגם בטבע (קראו עליו באאוריקה בתגית "חיתוך הזהב"). בקוואזי-גבישים מופיע חתך הזהב ביחס שבין המרחקים השונים שבין האטומים של הגבישים.
הנה סיפורם של הקוואזי-הקריסטלים של דן שכטמן:
https://youtu.be/TBaNHQKMoys
בשיר (עברית):
https://youtu.be/Z2E59W4OmI0
אנימציה של קוואזי-גבישים:
https://youtu.be/W_ufqM-V84o
ויחס הזהב עצמו מקורו בטבע (מתורגם):
https://youtu.be/_cIlomNxxig
 מה בין סימטריה ליופי?
מה בין סימטריה ליופי?
חוקרים רבים עסקו בנסיון לפצח את סוד היופי. מה נחשב בעינינו יפה? איך מזהים יופי מבחינה מדעית? האם מדובר בסימטריה? האם במשהו מיסטי?
נראה שרבים נוטים לראות ביופי משהו שככלשהו קרוב אל הממוצע בחברה מסוימת - הוא רב. לפיכך, על פי תפיסה זו, יוצאי דופן בחברה אינם יפים.
יש חוקרים הרואים יחס מתמטי מסוים כמה שמסביר את הדברים שאנשים תופסים כיפים. לדוגמה, נמצא שבהרבה מאד מקרים, "יחס הזהב" או "יחס חתך הזהב", מצוי במבנים או בפניהם של אנשים שהוגדרו יפים. יחס הזהב, הנקרא במתמטיקה "פִי" (1.618), קיים בטבע בדברים רבים. במקומות שונים בעולם עוסקים חוקרים בנסיונות להגדיר מדדים לבחינה של היופי האנושי, מדדים שמבוססים על סימטריה ועל פרופורציות של פנים העונים לחתך הזהב. דוגמאות כאלה יכולות להיות היחס שבין גובה הפנים לרוחב הפנים של אדם, היחס בין רוחב האף לרוחב הפה וכן הלאה.
פלורנס קולגייט, נערה בריטית צעירה, זכתה להגדרה מדעית של "האישה היפה באנגליה". מסתבר שבניתוח של אלפי פנים, נמצאו פניה בעלות סימטריה ופרופורציות מושלמות ביחס הזהב שבין המרכיבים השונים בפנים. שימו לב בסרטונים הבאים גם ליופי הטבעי של העלמה קולגייט וגם למדידות המתמטיות המדויקות שמסבירות אותו.
הנה סרטון על הכוח המרהיב של הסימטריה:
https://youtu.be/zwf2oyVhIY4
מפורסמים יפים להפליא הם אלה שמצוידים בתווי פנים סימטריים:
https://youtu.be/3sRXeGcNCrQ
חלוקת יחס הזהב וכמה שהיא נפוצה בפנים המושלמות מדעית, של פלורנס קולגייט:
http://youtu.be/kKWV-uU_SoI
ותכנית חינוכית לילדים על יופי ואמנות (עברית):
https://youtu.be/5IcpwZkOEfQ?long=yes
 מהו יחס הזהב או חיתוך הזהב?
מהו יחס הזהב או חיתוך הזהב?
מדהים שחשבון יכול להיות קשור ליופי, לא?
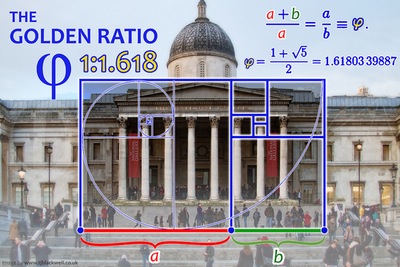
אינכם מאמינים? - את יחס הזהב גילה ככל הנראה אחד מתלמידיו של הפילוסוף היווני פִּיתָגוֹרַס לפני כ-2,500 שנה. הוא שם לב שבני האדם הכי אוהבים צורה של מלבן שהיחס בין צלעותיו הוא יחס חשבוני של 1 ל-1.618. היחס הזה שיוצר "מלבן הזהב", יחס שמתקבל מחלוקת האורך שלו ברוחבו, התגלה כיפה בעיני אנשים בכל העולם. זהו "יחס הזהב" או "חיתוך הזהב", שמופיע במקומות רבים ובלתי-צפויים.
מאז הסתבר במחקרים שאם היו אנשים רבים ומגוונים מכל העולם והתקופות נשאלים איזה מרובע מבין מספר מרובעים שלפניהם הוא היפה והנעים ביותר לעין, רובם ככולם היו בוחרים במלבן הזהב. זה מראה שהיופי הוא אובייקטיבי, כלומר לא תלוי בתקופה, תרבות או אמונה.
ואכן, יחס הזהב, שיש שהמכנים גם "חתך הזהב", הוא יחס מתמטי שהמדע והאמנות עוסקים בו כבר מאות בשנים. תלמידי המתמטיקה מכירים אותו בתור המספר האי רציונלי שמסומן באות היוונית 'פִי' (φ). זהו מספר שמתחיל ב-1.6180339887 אבל הוא מכיל מספר אינסופי של ספרות אחרי הנקודה העשרונית.
יחס הזהב, שתואר לראשונה לפני כ-2,300 שנים בספר "יסודות" של אוקלידס, כונה אז "יחס קיצוני וממוצע". בתקופת הרנסאנס נכתבו מחקרים וספרים על "יחס הזהב" והוא קיבל את הכינוי "הפרופורציה האלוהית". בנו לפיו מבנים מפוארים, יצרו יצירות אמנות נשגבות, הלחינו מוסיקה ובמיוחד ראו אותו בטבע, כמעט בכל מקום.
התבוננות במלבן הזהב ממלאת בני האדם בתחושה של יופי ופרופורציה. כשמחלקים את אורכו של מלבן הזהב ברוחבו מקבלים את "יחס הזהב". היוונים הקדמונים והמצרים הקדמונים התייחסו אליו כשיא היופי האסתטי ותכננו לפיו מבנים מהיפים ביותר בעולם העתיק, כולל הפירמידות במצרים והפרתנון שבאקרופוליס של אתונה. באומנות מופיע יחס הזהב ברבים מהציורים שבהם יש יחס פרופורציוני בין גדלים שונים.
כאמור, בנוסף לאמנות, אדריכלות ותחומי אסתטיקה אחרים שמשתמשים לא מעט ביחס הזהב, גם בטבע ניתן לראותו, במבנים של קונכיות ושבלולים, בסידור העלים מסביב לגבעולים, במערבולות, סופות טורנדו ועד לגלקסיות חלזוניות.
יש גם טענה שיחס הזהב הוא שמסביר את העובדה שאנו שכולנו מזהים את אותן פנים יפות ומבנה גוף יפה. כאן כמובן שיש מחלוקות, כי הוכח לא פעם שגם אם פנים שבנויות על פי יחס הזהב הן יפות, הרבה פנים שנחשבים יפים בקרב הציבור, כמו מרילין מונרו למשל, לא מחולקים על פי יחס הזהב.. האם הם מכוערים?
הנה סרטון הסבר על יחס הזהב (עברית):
https://youtu.be/co2k2bcZ1h0
יחס הזהב והקשר בינו לבין מה שאנו רואים כיופי (מתורגם):
http://youtu.be/_cIlomNxxig
יחס הזהב דרך סדרת פיבונאצ'י, בה יש בין כל שני מספרים יחס הנוטה ליחס הזהב (מתורגם):
http://youtu.be/z5RWfXTd3QU
איך יחס הזהב בונה את המלבנים שהקשתות שעוברות בהם יוצרות את סדרת פיבונאצ'י:
http://youtu.be/kkGeOWYOFoA
ההקשרים השונים של פי ויחס הזהב:
http://youtu.be/0hvD5kLqjuw
וסרט תיעודי על יחס הזהב:
https://youtu.be/gLml9nltl6M?long=yes
 איך נוצרת מערבולת?
איך נוצרת מערבולת?
כשחומר בצורת נוזל או גז זורם במעגל, נוצרת מערבולת (Whirlpool). מערבולות נוצרות לעתים בים וגם באוויר, בסופות טורנדו שיוצרות סחרור או ברוחות מדבריות שיוצרות עמוד חול, כמו עלעול החול.
במרכז המערבולת הזרימה מהירה יותר ממהירות זרימת החומר בשוליים. לשחיינים עלול להיות מסוכן מאד להיקלע למערבולת.
אגב, כמו תופעות טבע רבות, משבלולים ועד גלקסיות ענקיות ביקום, גם המערבולת היא מתופעות הטבע המתנהלות על פי חתך הזהב. זהו אותו יחס מתמטי מופלא שמתקיים הרבה בטבע. קראו עליו באאוריקה בתגית "יחס הזהב".
ואגב, לא רק במים יש מערבולות. גם באוויר יש אותן בצורה של מערבולות אוויר. אתם פוגשים אותן כשאתם טסים במטוס ומרגישים טלטלה פתאומית, וטרטור מתמשך ומטריד, שלא לומר מפחיד.
כך נוצרת המערבולת:
https://youtu.be/pnbJEg9r1o8
מערבולת מצולמת מהצד בים:
https://youtu.be/eBWqaamZ01I
מערבולות האוויר שבעולם (מתורגם):
https://youtu.be/S3i6tJ4XNqA
ובחזרה למים עם כמה מערבולות גדולות ומסוכנות במיוחד:
https://youtu.be/0v6VE4aNkN8?long=yes
 איך בנו את הפירמידות במצרים?
איך בנו את הפירמידות במצרים?
עוד מימי העת העתיקה נחשבות הפירמידות במצרים לפלא אמיתי. במשך שנים רבות לא הצליחו החוקרים להבין כיצד ניתן היה לבנות מבנים עצומים שכאלה בעזרת הטכנולוגיה של הזמן העתיק. החוקרים טוענים שהמצרים בנו פירמידות, על ידי בנייה של סוללת ענק חזיתית שגובהה הלך ועלה. הייתה מגבלה לגובה של סוללה שכזו ולכן לבניית החלק העליון של הפירמידה הגדולה של גיזה, נדרשה עוד סוללה פנימית סיבובית, בת 100 מטרים נוספים.
חוקרים אחרים העריכו שהסוללה שבנו לצורך העמסת האבנים הייתה לוליינית דווקא ונבנתה מסביב למקום הפירמידה. כך ניתן היה לגרור את האבנים העצומות לגובה הרצוי.
גם לגבי גרירת האבנים אל הפירמידה יש שאלות הנדסיות. תיאוריה שמדברת על "חול רטוב" מסבירה את האפשרות לגרור את אבני הענק לצורך בניית הפירמידה. באמצעות מים שהרטיבו את החול ניתן היה להעביר אבנים גדולות במאמץ קטן יותר. שחזור שנעשה בידי פועלים בני זמננו הדגים זאת.
בכל מקרה, דומה שהדיון על שיטות הבנייה והטכנולוגיות המצריות הקדמוניות עוד לא הסתיים. ואגב, גם בתכנון, במקרה או לא, המצרים הקדמונים תכננו את הפירמידות על פי הפרופורציות המלבניות של "יחס הזהב", יחס מתמטי שמסתבר שאמנים ואדריכלים רבים לאורך ההיסטוריה אימצו כמודל יופי והוא זכה אף לכינוי "הפרופורציה האלוהית". תוכלו לקרוא עליו באאוריקה, בתגית "יחס הזהב".
הנה הסבר פשוט לבניית הפירמידות וכיצד בני ישראל קשורים, אם בכלל (עברית):
https://youtu.be/yor-TywKHDU
כך נבנתה הפירמידה הגדולה של ח'ופו (מתורגם):
https://youtu.be/fJBlEPOj4Fk
המסתורין סביב הפירמידות וכיצד סייעו ציורים מצריים להבין את טכניקת הבנייה:
https://youtu.be/LBF2pHH6f9A
עוד על בניית הפירמידות:
https://youtu.be/zfYFwXqknjM
הסבר אפשרי נוסף על הדרך שבה העבירו והעלו את אבני הענק לראש הפירמידה:
https://youtu.be/dGH93mt81BA?t=13s
וניסיון מעמיק ושונה להסביר כיצד בנו את הפירמידות:
http://youtu.be/TJcp13hAO3U
 מהן גלקסיות לולייניות?
מהן גלקסיות לולייניות?
גלקסיית שביל החלב, הגלקסיה שבה נמצא כדור הארץ היא גלקסיה ספירלית, חלזונית. גם הגלקסיה השכנה, גלקסיית אנדרומדה, שייכת לסוג זה. גלקסיות ספירליות, או גלקסיות לולייניות, הן גלקסיות שיש להן צורה לוליינית, דמוית חילזון. במרכז של גלקסיה כזו יש מעין עיגול שטוח בצורת דיסקה ולו זרועות שיוצרות מבנה ספירלי.
הצורה האופיינית לגלקסיות כאלה היא של חילזון והיא מתקבלת מהאופן שבו נעים הכוכבים בגלקסיה, צורת תנועה שהיא אמנם אטית מאוד ונמדדת במשכי זמן של מאות מיליוני שנים, אך בבסיסה היא דומה לתנועה של המים במערבולות מים, לתנועת האוויר בסופות טורנדו או לחול הנע בעמודי חול כמו עלעול.
כמו בחלזונות וביצירות אמנות, מבנים אדריכליים ויצירות מוסיקליות מרתקות, מדהים לגלות שגם בצורתן של גלקסיות כאלה, על מיליארדי הכוכבים שבהן, ניתן לראות את היחס המתמטי המופלא של "חיתוך הזהב" (או "יחס הזהב"). יחס מופלא זה, שמתקבל מחלוקת האורך של מלבן הזהב ברוחב שלו, זכה לשם "הפרופורציה האלוהית". קראו עליו באאוריקה בתגית "יחס הזהב".
ברוב המקרים נמצאות הגלקסיות הספירליות בשולי צבירי גלקסיות ולא במרכזן.
הנה הגלקסיות הלולייניות:
https://youtu.be/5sGKuoBnTn0
תצוגה גרפית של גלקסיית שביל החלב הספירלית:
https://youtu.be/C4V-ooITrws?t=30s
התבוננות בפרטים בצילום של M81 - גלקסיה חלזונית מרוחקת הנמצאת מעל 11 מיליון שנות אור מכדור הארץ:
https://youtu.be/0seVq5ydqzk
הדגמת מחשב של היווצרות גלקסיה לוליינית (במהירות מואצת כמובן, כי במציאות התהליך נמשך מיליוני שנים):
https://youtu.be/LTlSLVbYFso
עוד אחת:
https://youtu.be/hVNuwAtnKeg
והצגה של המבנה הפרקטלי של הגלקסיה החלזונית וכמה שהוא דומה למבנים טבעיים רבים:
https://youtu.be/vGq3x31ex1Y
 מהו מלבן הזהב?
מהו מלבן הזהב?
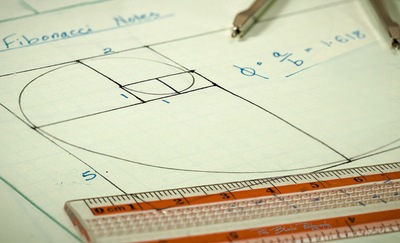
מסתבר שאם היו אנשים רבים ומגוונים מכל העולם והתקופות נשאלים איזה מרובע מבין מספר מרובעים שלפניהם הוא היפה והנעים ביותר לעין, היו בוחרים רובם ככולם במלבן הזהב. מלבן הזהב הוא מלבן שהיחס בין אורכו לרוחבו הוא יחס שזכה גם הוא לכינוי יחס הזהב. כשהאורך של מלבן גדול פי בערך 1.618 מהרוחב שלו, מתקיים יחס מושלם ביניהם והוא נקרא מלבן הזהב. מלבן הזהב מוכיח שהיופי הוא אובייקטיבי, כלומר לא תלוי בתקופה, תרבות או אמונה.
כיוון שיחס הזהב הוא כה יפה ומושלם בעיני המתבוננים, הוא זכה לכינוי 'הפרופורציה האלוהית'. אלא שיחס הזהב נמצא כנכון ומתאים לא רק באומנות שעשה האדם, אלא קודם כל בטבע עצמו. כי מעולם הטבע הגיע יחס הזהב והמספר פי לעולם האומנות. ומאז ומתמיד הוא מופיע באדריכלות, במבנים המושלמים והיפים בהיסטוריה, ובאומנות - ברבים מהציורים שבהם יש יחס פרופורציוני בין גדלים שונים.
עמים קדומים כמו היוונים הקדמונים והמצרים הקדמונים התייחסו למלבן הזהב כשיא היופי האסתטי ותכננו לפיו מבנים מהיפים ביותר בעולם העתיק. בין המבנים שבנויים בהקפדה של יחס הזהב או מלבן הזהב, ניתן למצוא את הפירמידות במצרים, הפרתנון שבאקרופוליס של אתונה הטאג' מהאל שבהודו.
הנה מלבן הזהב שיוצר את הספירלות המיוחדות כל כך על פי יחס הזהב:
http://youtu.be/kkGeOWYOFoA
המתמטיקה של יחס הזהב (עברית):
https://youtu.be/co2k2bcZ1h0
ההופעות הרבות של יחס הזהב ומלבן הזהב:
http://youtu.be/0hvD5kLqjuw
והמקומות המפתיעים מסביב שבהם ניתן לפגוש אותו:
https://youtu.be/RqqErDSLtwE?long=yes
 מה הפלא המתמטי של החמניה?
מה הפלא המתמטי של החמניה?
לאונרדו מפיזה, או פיבונאצ'י כמו שקרא לעצמו, היה כנראה גדול המתמטיקאים של ימי הביניים. במיוחד הוא ידוע כמי שגילה את סדרת המספרים המכונה על שמו "סדרת פיבונאצ'י".
כל איבר בסדרת פיבונאצ'י שווה לסכום של שני האיברים הקודמים לו. הוא לא הפסיק להתפעל מהקסם המתמטי של הסדרה הזו, כמו זה שביחסים בין ריבועי המספרים או ביופי של מה שהיא יוצרת בגאומטריה למשל, אבל אפילו הוא לא שיער כמה תופעות טבע מאופיינות במספרי פיבונאצ'י, כמו למשל העובדה שמספר עלי הכותרת בצמחים רבים הוא תמיד מספר פיבונצ'י, כמו 5, 8, 13 וכדומה.
מפתיע? - אז שימו לב לתופעה מרתקת אפילו יותר.. מסתבר שמספר הגרעינים שבפרח החמניה הם מספרי פיבונצ'י עוקבים. אם תביטו היטב, הם נראים כמו 2 ספירלות, שאחת היא בעלת 89 גרעינים והשנייה בת 55 גרעינים - שני מספרים עוקבים בסדרה (אגב, זה כך גם באצטרובלי עץ האורן).
ולמה זה קורה? - ובכן, נראה שהספירלות הללו מופיעות בפרחים כאלה ובאיצטרובלים, כדי למנוע מצב שבו הגרעינים יהיו צפופים מדי ויתקשו להתפתח. לכן הטבע מרבה אותם במספרי פיבונצ'י וכך נוצר המספר המרבי של גרעינים, מה שיבטיח שכפול מוצלח והמשך הדורות.
וזה לא הדבר היחיד שבו פיבונצ'י נראה בצמחים כאלו. מסתבר שאפילו זווית הגדילה של העלים על הגבעול, זו שמאפשרת לעלים החדשים לצמוח באופן שיקבלו הכי הרבה אור שמש, אפילו היא מתמטית ומדויקת. למעשה היא ידועה בתור יחס הזהב, כ-1.618. אם נחלק 360 מעלות של הגבעול העגול במספר 1.618 נקבל בדיוק את המיקומים שהטבע בחר לגדילת העלים על הגבעול. בינגו! - שוב הטבע הצטיין במתמטיקה והשתמש במספרי פיבונצ'י וביחס הזהב שנובע ממנו כדי להיטיב את גדילת הצמחים.
אז האמת שאין כאן פלא, חוץ מפלאי הטבע כמובן. סדרת פיבונאצ'י, שאנו כה מתפעלים ממנה כאן, היא הדרך שבה מאורגנים ומשוכפלים ביעילות מרכיבים רבים בטבע ובה פועלים ביעילות רבה כוחות טבעיים שונים. כשאנו מוצאים בחמניה את מספרי פיבונאצ'י, לכל היותר נוכל לומר שהחמניה "גדלה כמו שצריך".. אז אולי זה מופלא, אבל לא יותר מהפלא הבלתי נתפס של היקום כולו!
הנה המתמטיקה של החמניות:
https://youtu.be/z9d1mxgZ0ag
היופי המתמטי שגלום בסדרת מספרים פשוטה לכאורה זו (מתורגם):
https://youtu.be/SjSHVDfXHQ4
והגרעינים האלה שעל פרח החמנייה - ככה הם הופכים לגרעינים שחורים (עברית):
https://youtu.be/xLCkC0oOFqw
 מי היה פיבונאצ'י ובאיזו סדרה הוא שיחק?
מי היה פיבונאצ'י ובאיזו סדרה הוא שיחק?
לאונרדו דה פיזה, מתמטיקאי מהעיר פיזה, כונה פשוט "פיבונאצ'י". פיבונאצ'י הוא זה שהביא לאירופה את הספרות ההודיות-ערביות, במקום הספרות הרומיות ששימשו את האירופאים עד אז. האמת היא שהעיסוק שלו בדברים שהסביבה לא הבינה, הוציא לו שם של ברנש מוזר. גם חתימתו בתור "הטייל" הוציאה לו שם של שוטה, שכן המילה משמשת גם לשוטים.
אך הוא עצמו עסק במתמטיקה מורכבת במיוחד. בהמשך חייו הוא אכן תרם למתמטיקה ולמדע את תרומתו האדירה, כשזיהה את "סדרת פיבונאצ'י", סדרת מספרים מופלאה שכל מספר הוא סכום הקודמים לו.
הצגת הסדרה וההגיון שבה פתחו פתח לזיהוי היחסים המדהימים שבין יופיים של הטבע והאמנות לבין הסדר המתמטי המדהים שבהם, סדר שהוגדר על ידי רבים כלא פחות מאשר "הפרופורציה האלוהית" (ראו באאוריקה בתגית "סדרת פיבונאצ'י"). בפשטות נאמר שזוהי סדרת מספרים שאם נחלק כל מספר בה במספר שקדם לו, נלך ונתקרב למספר 1.618. זהו המספר הידוע במתמטיקה, מאז היוונים הקדמונים, בתור "פיי" ("Phi"). אנו קוראים לו יחס הזהב והיוונים קשרו אותו אל היופי המושלם.
פיבונאצ'י הסביר שבמיני פרחים שונים ובאיצטרובלים - לאן שהביט הוא גילה בטבע את הצורות של הסדרה המתמטית שהציג. הוא גם זיהה את "מלבן הזהב" שנמצא בזרעי החמניות, בקונכיות, שבלולים, בצמחים סוקולנטיים, מיצירות אמנות ועד גלקסיות חלזוניות. חוקרים רבים אחריו גילו עד כמה נמצאים סדרת פיבונאצ'י ויחס הזהב בכל מקום.
כיום נחשב פיבונאצ'י בעיני רבים לגדול המתמטיקאים של ימי הביניים.
הנה סיפורו של פיבונאצי והסדרה המתמטית המופלאה שמצא (עברית):
https://youtu.be/EAXKR-H_bS0?t=8s
סרטון על לאונרדו פיבונצ'י:
http://youtu.be/wTlw7fNcO-0
הסבר לסדרת פיבונצ'י (מתורגם):
http://youtu.be/z5RWfXTd3QU
וסרט תיעודי על לאונרדו פיבונצ'י:
https://youtu.be/O2wU-HT7FiM?long=yes

תגליתו הגדולה של זוכה פרס נובל הישראלי דן שכטמן הם הגבישים הכמו-מחזוריים או בשפת הכימאים "קוואזי-גבישים" (quasicrystals) או "גביש קווזיפריודי".
הכל התחיל בבוקר אחד בחודש אפריל 1982. כשהביט במיקרוסקופ האלקטרוני שלו, ראה דן שכטמן סידור אטומים שהיה מנוגד לחלוטין לחוקי הטבע. הוא הרי למד תמיד שהאטומים שבגבישים מוצקים יוצרים תמיד תבניות סימטריות, שחוזרות על עצמן שוב ושוב, באופן מחזורי. התבניות שהוא ראה היו סדירות ותואמות את חוקי המתמטיקה, אך הן לא חזרו על עצמן אף פעם.
שכטמן גילה גביש כמו-מחזורי. בניגוד לגבישים רגילים, שהם בעלי סריג מחזורי, הגביש הכמו-מחזורי הוא בעל סימטריה בתבניות סדורות שלא חוזרות על עצמן אף פעם. בקוואזי-גבישים כאלו ראה שכטמן מעין פסיפסים שהזכירו לו את הפסיפסים והעיטורים שמקובלים באמנות הערבית מאז ימי הביניים, כאלה שניתן לראות במסגדים ובארמונות ערביים, מארמון אלהמברה שבדרום ספרד ועד ארמונות הפאר שבאיראן. אלא שבקוואזי-גביש הם משוכפלים פעם אחר פעם ברמת האטום!
כשפרסם שכטמן את ממצאיו טענו חוקרים ומומחים בתחום שהתצורה שגילה היא בלתי אפשרית ולא הגיונית. הכימאים התרגלו שהחזרה והמחזוריות הן חלק בלתי נפרד מהמבנה של הגביש וכאן בא המדען הישראלי וטוען שלא כך הדברים. הוא מצא את עצמו במוקד של מתקפה מדעית. במשך שנים רבות נאלץ להיאבק כנגד המומחים והידע המקובל בתחום המדעי. במהלך המאבק, שלא תמיד היה נעים, הוא מצא עצמו מגורש מקבוצת המחקר שלו. קביעותיו המדעיות נראו לרבים בעייתיות, אבל הוא עמד על שלו וסיפק הסברים וממצאים שהלכו וחיזקו את דעתו.
טיפין טיפין החלו הדעות משתנות. דן שכטמן אילץ את עולם הכימיה לשקול מחדש את התפיסה המקובלת בנוגע לטיבו הבסיסי של החומר. כשזכה בשנת 2011 בפרס נובל לכימיה על תגלית זו, הוא קיבל סוג של הכרה בכך שהוא ניצח במאבקו והצליח לשנות את הדעה המקובלת לגבי הכימיה של חומרים מוצקים.
כיום נמצאו הוכחות רבות לממצאיו של שכטמן. מדען אחד מצא את הגבישים הללו במינרלים שהוציא מנהר רוסי. מדענים אחרים יצרו גבישים קריסטליים כאלו באופן מלאכותי במעבדה. חוקרים אחרים מצאו שהקוואזי גבישים מחזקים את סוגי פלדה מסוימים והופכים אותה מחושלת וחזקה במיוחד. גם התעשייה כבר נערכת להשתמש בגבישים הללו לייצור של מכשירים חזקים מאי-פעם.
מדענים רבים מצאו בקוואזי-גבישים של שכטמן את "יחס הזהב", או בשמו הנוסף "חיתוך הזהב". היחס זה, שמאז יוון העתיקה השתמשו בו אדריכלים, אמנים ומהנדסים בתרבויות שונות ובהקשרים מגוונים, מופיע גם בגיאומטריה וגם בטבע (קראו עליו באאוריקה בתגית "חיתוך הזהב"). בקוואזי-גבישים מופיע חתך הזהב ביחס שבין המרחקים השונים שבין האטומים של הגבישים.
הנה סיפורם של הקוואזי-הקריסטלים של דן שכטמן:
https://youtu.be/TBaNHQKMoys
בשיר (עברית):
https://youtu.be/Z2E59W4OmI0
אנימציה של קוואזי-גבישים:
https://youtu.be/W_ufqM-V84o
ויחס הזהב עצמו מקורו בטבע (מתורגם):
https://youtu.be/_cIlomNxxig

חוקרים רבים עסקו בנסיון לפצח את סוד היופי. מה נחשב בעינינו יפה? איך מזהים יופי מבחינה מדעית? האם מדובר בסימטריה? האם במשהו מיסטי?
נראה שרבים נוטים לראות ביופי משהו שככלשהו קרוב אל הממוצע בחברה מסוימת - הוא רב. לפיכך, על פי תפיסה זו, יוצאי דופן בחברה אינם יפים.
יש חוקרים הרואים יחס מתמטי מסוים כמה שמסביר את הדברים שאנשים תופסים כיפים. לדוגמה, נמצא שבהרבה מאד מקרים, "יחס הזהב" או "יחס חתך הזהב", מצוי במבנים או בפניהם של אנשים שהוגדרו יפים. יחס הזהב, הנקרא במתמטיקה "פִי" (1.618), קיים בטבע בדברים רבים. במקומות שונים בעולם עוסקים חוקרים בנסיונות להגדיר מדדים לבחינה של היופי האנושי, מדדים שמבוססים על סימטריה ועל פרופורציות של פנים העונים לחתך הזהב. דוגמאות כאלה יכולות להיות היחס שבין גובה הפנים לרוחב הפנים של אדם, היחס בין רוחב האף לרוחב הפה וכן הלאה.
פלורנס קולגייט, נערה בריטית צעירה, זכתה להגדרה מדעית של "האישה היפה באנגליה". מסתבר שבניתוח של אלפי פנים, נמצאו פניה בעלות סימטריה ופרופורציות מושלמות ביחס הזהב שבין המרכיבים השונים בפנים. שימו לב בסרטונים הבאים גם ליופי הטבעי של העלמה קולגייט וגם למדידות המתמטיות המדויקות שמסבירות אותו.
הנה סרטון על הכוח המרהיב של הסימטריה:
https://youtu.be/zwf2oyVhIY4
מפורסמים יפים להפליא הם אלה שמצוידים בתווי פנים סימטריים:
https://youtu.be/3sRXeGcNCrQ
חלוקת יחס הזהב וכמה שהיא נפוצה בפנים המושלמות מדעית, של פלורנס קולגייט:
http://youtu.be/kKWV-uU_SoI
ותכנית חינוכית לילדים על יופי ואמנות (עברית):
https://youtu.be/5IcpwZkOEfQ?long=yes

מדהים שחשבון יכול להיות קשור ליופי, לא?
אינכם מאמינים? - את יחס הזהב גילה ככל הנראה אחד מתלמידיו של הפילוסוף היווני פִּיתָגוֹרַס לפני כ-2,500 שנה. הוא שם לב שבני האדם הכי אוהבים צורה של מלבן שהיחס בין צלעותיו הוא יחס חשבוני של 1 ל-1.618. היחס הזה שיוצר "מלבן הזהב", יחס שמתקבל מחלוקת האורך שלו ברוחבו, התגלה כיפה בעיני אנשים בכל העולם. זהו "יחס הזהב" או "חיתוך הזהב", שמופיע במקומות רבים ובלתי-צפויים.
מאז הסתבר במחקרים שאם היו אנשים רבים ומגוונים מכל העולם והתקופות נשאלים איזה מרובע מבין מספר מרובעים שלפניהם הוא היפה והנעים ביותר לעין, רובם ככולם היו בוחרים במלבן הזהב. זה מראה שהיופי הוא אובייקטיבי, כלומר לא תלוי בתקופה, תרבות או אמונה.
ואכן, יחס הזהב, שיש שהמכנים גם "חתך הזהב", הוא יחס מתמטי שהמדע והאמנות עוסקים בו כבר מאות בשנים. תלמידי המתמטיקה מכירים אותו בתור המספר האי רציונלי שמסומן באות היוונית 'פִי' (φ). זהו מספר שמתחיל ב-1.6180339887 אבל הוא מכיל מספר אינסופי של ספרות אחרי הנקודה העשרונית.
יחס הזהב, שתואר לראשונה לפני כ-2,300 שנים בספר "יסודות" של אוקלידס, כונה אז "יחס קיצוני וממוצע". בתקופת הרנסאנס נכתבו מחקרים וספרים על "יחס הזהב" והוא קיבל את הכינוי "הפרופורציה האלוהית". בנו לפיו מבנים מפוארים, יצרו יצירות אמנות נשגבות, הלחינו מוסיקה ובמיוחד ראו אותו בטבע, כמעט בכל מקום.
התבוננות במלבן הזהב ממלאת בני האדם בתחושה של יופי ופרופורציה. כשמחלקים את אורכו של מלבן הזהב ברוחבו מקבלים את "יחס הזהב". היוונים הקדמונים והמצרים הקדמונים התייחסו אליו כשיא היופי האסתטי ותכננו לפיו מבנים מהיפים ביותר בעולם העתיק, כולל הפירמידות במצרים והפרתנון שבאקרופוליס של אתונה. באומנות מופיע יחס הזהב ברבים מהציורים שבהם יש יחס פרופורציוני בין גדלים שונים.
כאמור, בנוסף לאמנות, אדריכלות ותחומי אסתטיקה אחרים שמשתמשים לא מעט ביחס הזהב, גם בטבע ניתן לראותו, במבנים של קונכיות ושבלולים, בסידור העלים מסביב לגבעולים, במערבולות, סופות טורנדו ועד לגלקסיות חלזוניות.
יש גם טענה שיחס הזהב הוא שמסביר את העובדה שאנו שכולנו מזהים את אותן פנים יפות ומבנה גוף יפה. כאן כמובן שיש מחלוקות, כי הוכח לא פעם שגם אם פנים שבנויות על פי יחס הזהב הן יפות, הרבה פנים שנחשבים יפים בקרב הציבור, כמו מרילין מונרו למשל, לא מחולקים על פי יחס הזהב.. האם הם מכוערים?
הנה סרטון הסבר על יחס הזהב (עברית):
https://youtu.be/co2k2bcZ1h0
יחס הזהב והקשר בינו לבין מה שאנו רואים כיופי (מתורגם):
http://youtu.be/_cIlomNxxig
יחס הזהב דרך סדרת פיבונאצ'י, בה יש בין כל שני מספרים יחס הנוטה ליחס הזהב (מתורגם):
http://youtu.be/z5RWfXTd3QU
איך יחס הזהב בונה את המלבנים שהקשתות שעוברות בהם יוצרות את סדרת פיבונאצ'י:
http://youtu.be/kkGeOWYOFoA
ההקשרים השונים של פי ויחס הזהב:
http://youtu.be/0hvD5kLqjuw
וסרט תיעודי על יחס הזהב:
https://youtu.be/gLml9nltl6M?long=yes

כשחומר בצורת נוזל או גז זורם במעגל, נוצרת מערבולת (Whirlpool). מערבולות נוצרות לעתים בים וגם באוויר, בסופות טורנדו שיוצרות סחרור או ברוחות מדבריות שיוצרות עמוד חול, כמו עלעול החול.
במרכז המערבולת הזרימה מהירה יותר ממהירות זרימת החומר בשוליים. לשחיינים עלול להיות מסוכן מאד להיקלע למערבולת.
אגב, כמו תופעות טבע רבות, משבלולים ועד גלקסיות ענקיות ביקום, גם המערבולת היא מתופעות הטבע המתנהלות על פי חתך הזהב. זהו אותו יחס מתמטי מופלא שמתקיים הרבה בטבע. קראו עליו באאוריקה בתגית "יחס הזהב".
ואגב, לא רק במים יש מערבולות. גם באוויר יש אותן בצורה של מערבולות אוויר. אתם פוגשים אותן כשאתם טסים במטוס ומרגישים טלטלה פתאומית, וטרטור מתמשך ומטריד, שלא לומר מפחיד.
כך נוצרת המערבולת:
https://youtu.be/pnbJEg9r1o8
מערבולת מצולמת מהצד בים:
https://youtu.be/eBWqaamZ01I
מערבולות האוויר שבעולם (מתורגם):
https://youtu.be/S3i6tJ4XNqA
ובחזרה למים עם כמה מערבולות גדולות ומסוכנות במיוחד:
https://youtu.be/0v6VE4aNkN8?long=yes
חתך הזהב

עוד מימי העת העתיקה נחשבות הפירמידות במצרים לפלא אמיתי. במשך שנים רבות לא הצליחו החוקרים להבין כיצד ניתן היה לבנות מבנים עצומים שכאלה בעזרת הטכנולוגיה של הזמן העתיק. החוקרים טוענים שהמצרים בנו פירמידות, על ידי בנייה של סוללת ענק חזיתית שגובהה הלך ועלה. הייתה מגבלה לגובה של סוללה שכזו ולכן לבניית החלק העליון של הפירמידה הגדולה של גיזה, נדרשה עוד סוללה פנימית סיבובית, בת 100 מטרים נוספים.
חוקרים אחרים העריכו שהסוללה שבנו לצורך העמסת האבנים הייתה לוליינית דווקא ונבנתה מסביב למקום הפירמידה. כך ניתן היה לגרור את האבנים העצומות לגובה הרצוי.
גם לגבי גרירת האבנים אל הפירמידה יש שאלות הנדסיות. תיאוריה שמדברת על "חול רטוב" מסבירה את האפשרות לגרור את אבני הענק לצורך בניית הפירמידה. באמצעות מים שהרטיבו את החול ניתן היה להעביר אבנים גדולות במאמץ קטן יותר. שחזור שנעשה בידי פועלים בני זמננו הדגים זאת.
בכל מקרה, דומה שהדיון על שיטות הבנייה והטכנולוגיות המצריות הקדמוניות עוד לא הסתיים. ואגב, גם בתכנון, במקרה או לא, המצרים הקדמונים תכננו את הפירמידות על פי הפרופורציות המלבניות של "יחס הזהב", יחס מתמטי שמסתבר שאמנים ואדריכלים רבים לאורך ההיסטוריה אימצו כמודל יופי והוא זכה אף לכינוי "הפרופורציה האלוהית". תוכלו לקרוא עליו באאוריקה, בתגית "יחס הזהב".
הנה הסבר פשוט לבניית הפירמידות וכיצד בני ישראל קשורים, אם בכלל (עברית):
https://youtu.be/yor-TywKHDU
כך נבנתה הפירמידה הגדולה של ח'ופו (מתורגם):
https://youtu.be/fJBlEPOj4Fk
המסתורין סביב הפירמידות וכיצד סייעו ציורים מצריים להבין את טכניקת הבנייה:
https://youtu.be/LBF2pHH6f9A
עוד על בניית הפירמידות:
https://youtu.be/zfYFwXqknjM
הסבר אפשרי נוסף על הדרך שבה העבירו והעלו את אבני הענק לראש הפירמידה:
https://youtu.be/dGH93mt81BA?t=13s
וניסיון מעמיק ושונה להסביר כיצד בנו את הפירמידות:
http://youtu.be/TJcp13hAO3U

גלקסיית שביל החלב, הגלקסיה שבה נמצא כדור הארץ היא גלקסיה ספירלית, חלזונית. גם הגלקסיה השכנה, גלקסיית אנדרומדה, שייכת לסוג זה. גלקסיות ספירליות, או גלקסיות לולייניות, הן גלקסיות שיש להן צורה לוליינית, דמוית חילזון. במרכז של גלקסיה כזו יש מעין עיגול שטוח בצורת דיסקה ולו זרועות שיוצרות מבנה ספירלי.
הצורה האופיינית לגלקסיות כאלה היא של חילזון והיא מתקבלת מהאופן שבו נעים הכוכבים בגלקסיה, צורת תנועה שהיא אמנם אטית מאוד ונמדדת במשכי זמן של מאות מיליוני שנים, אך בבסיסה היא דומה לתנועה של המים במערבולות מים, לתנועת האוויר בסופות טורנדו או לחול הנע בעמודי חול כמו עלעול.
כמו בחלזונות וביצירות אמנות, מבנים אדריכליים ויצירות מוסיקליות מרתקות, מדהים לגלות שגם בצורתן של גלקסיות כאלה, על מיליארדי הכוכבים שבהן, ניתן לראות את היחס המתמטי המופלא של "חיתוך הזהב" (או "יחס הזהב"). יחס מופלא זה, שמתקבל מחלוקת האורך של מלבן הזהב ברוחב שלו, זכה לשם "הפרופורציה האלוהית". קראו עליו באאוריקה בתגית "יחס הזהב".
ברוב המקרים נמצאות הגלקסיות הספירליות בשולי צבירי גלקסיות ולא במרכזן.
הנה הגלקסיות הלולייניות:
https://youtu.be/5sGKuoBnTn0
תצוגה גרפית של גלקסיית שביל החלב הספירלית:
https://youtu.be/C4V-ooITrws?t=30s
התבוננות בפרטים בצילום של M81 - גלקסיה חלזונית מרוחקת הנמצאת מעל 11 מיליון שנות אור מכדור הארץ:
https://youtu.be/0seVq5ydqzk
הדגמת מחשב של היווצרות גלקסיה לוליינית (במהירות מואצת כמובן, כי במציאות התהליך נמשך מיליוני שנים):
https://youtu.be/LTlSLVbYFso
עוד אחת:
https://youtu.be/hVNuwAtnKeg
והצגה של המבנה הפרקטלי של הגלקסיה החלזונית וכמה שהוא דומה למבנים טבעיים רבים:
https://youtu.be/vGq3x31ex1Y

מסתבר שאם היו אנשים רבים ומגוונים מכל העולם והתקופות נשאלים איזה מרובע מבין מספר מרובעים שלפניהם הוא היפה והנעים ביותר לעין, היו בוחרים רובם ככולם במלבן הזהב. מלבן הזהב הוא מלבן שהיחס בין אורכו לרוחבו הוא יחס שזכה גם הוא לכינוי יחס הזהב. כשהאורך של מלבן גדול פי בערך 1.618 מהרוחב שלו, מתקיים יחס מושלם ביניהם והוא נקרא מלבן הזהב. מלבן הזהב מוכיח שהיופי הוא אובייקטיבי, כלומר לא תלוי בתקופה, תרבות או אמונה.
כיוון שיחס הזהב הוא כה יפה ומושלם בעיני המתבוננים, הוא זכה לכינוי 'הפרופורציה האלוהית'. אלא שיחס הזהב נמצא כנכון ומתאים לא רק באומנות שעשה האדם, אלא קודם כל בטבע עצמו. כי מעולם הטבע הגיע יחס הזהב והמספר פי לעולם האומנות. ומאז ומתמיד הוא מופיע באדריכלות, במבנים המושלמים והיפים בהיסטוריה, ובאומנות - ברבים מהציורים שבהם יש יחס פרופורציוני בין גדלים שונים.
עמים קדומים כמו היוונים הקדמונים והמצרים הקדמונים התייחסו למלבן הזהב כשיא היופי האסתטי ותכננו לפיו מבנים מהיפים ביותר בעולם העתיק. בין המבנים שבנויים בהקפדה של יחס הזהב או מלבן הזהב, ניתן למצוא את הפירמידות במצרים, הפרתנון שבאקרופוליס של אתונה הטאג' מהאל שבהודו.
הנה מלבן הזהב שיוצר את הספירלות המיוחדות כל כך על פי יחס הזהב:
http://youtu.be/kkGeOWYOFoA
המתמטיקה של יחס הזהב (עברית):
https://youtu.be/co2k2bcZ1h0
ההופעות הרבות של יחס הזהב ומלבן הזהב:
http://youtu.be/0hvD5kLqjuw
והמקומות המפתיעים מסביב שבהם ניתן לפגוש אותו:
https://youtu.be/RqqErDSLtwE?long=yes

לאונרדו מפיזה, או פיבונאצ'י כמו שקרא לעצמו, היה כנראה גדול המתמטיקאים של ימי הביניים. במיוחד הוא ידוע כמי שגילה את סדרת המספרים המכונה על שמו "סדרת פיבונאצ'י".
כל איבר בסדרת פיבונאצ'י שווה לסכום של שני האיברים הקודמים לו. הוא לא הפסיק להתפעל מהקסם המתמטי של הסדרה הזו, כמו זה שביחסים בין ריבועי המספרים או ביופי של מה שהיא יוצרת בגאומטריה למשל, אבל אפילו הוא לא שיער כמה תופעות טבע מאופיינות במספרי פיבונאצ'י, כמו למשל העובדה שמספר עלי הכותרת בצמחים רבים הוא תמיד מספר פיבונצ'י, כמו 5, 8, 13 וכדומה.
מפתיע? - אז שימו לב לתופעה מרתקת אפילו יותר.. מסתבר שמספר הגרעינים שבפרח החמניה הם מספרי פיבונצ'י עוקבים. אם תביטו היטב, הם נראים כמו 2 ספירלות, שאחת היא בעלת 89 גרעינים והשנייה בת 55 גרעינים - שני מספרים עוקבים בסדרה (אגב, זה כך גם באצטרובלי עץ האורן).
ולמה זה קורה? - ובכן, נראה שהספירלות הללו מופיעות בפרחים כאלה ובאיצטרובלים, כדי למנוע מצב שבו הגרעינים יהיו צפופים מדי ויתקשו להתפתח. לכן הטבע מרבה אותם במספרי פיבונצ'י וכך נוצר המספר המרבי של גרעינים, מה שיבטיח שכפול מוצלח והמשך הדורות.
וזה לא הדבר היחיד שבו פיבונצ'י נראה בצמחים כאלו. מסתבר שאפילו זווית הגדילה של העלים על הגבעול, זו שמאפשרת לעלים החדשים לצמוח באופן שיקבלו הכי הרבה אור שמש, אפילו היא מתמטית ומדויקת. למעשה היא ידועה בתור יחס הזהב, כ-1.618. אם נחלק 360 מעלות של הגבעול העגול במספר 1.618 נקבל בדיוק את המיקומים שהטבע בחר לגדילת העלים על הגבעול. בינגו! - שוב הטבע הצטיין במתמטיקה והשתמש במספרי פיבונצ'י וביחס הזהב שנובע ממנו כדי להיטיב את גדילת הצמחים.
אז האמת שאין כאן פלא, חוץ מפלאי הטבע כמובן. סדרת פיבונאצ'י, שאנו כה מתפעלים ממנה כאן, היא הדרך שבה מאורגנים ומשוכפלים ביעילות מרכיבים רבים בטבע ובה פועלים ביעילות רבה כוחות טבעיים שונים. כשאנו מוצאים בחמניה את מספרי פיבונאצ'י, לכל היותר נוכל לומר שהחמניה "גדלה כמו שצריך".. אז אולי זה מופלא, אבל לא יותר מהפלא הבלתי נתפס של היקום כולו!
הנה המתמטיקה של החמניות:
https://youtu.be/z9d1mxgZ0ag
היופי המתמטי שגלום בסדרת מספרים פשוטה לכאורה זו (מתורגם):
https://youtu.be/SjSHVDfXHQ4
והגרעינים האלה שעל פרח החמנייה - ככה הם הופכים לגרעינים שחורים (עברית):
https://youtu.be/xLCkC0oOFqw

לאונרדו דה פיזה, מתמטיקאי מהעיר פיזה, כונה פשוט "פיבונאצ'י". פיבונאצ'י הוא זה שהביא לאירופה את הספרות ההודיות-ערביות, במקום הספרות הרומיות ששימשו את האירופאים עד אז. האמת היא שהעיסוק שלו בדברים שהסביבה לא הבינה, הוציא לו שם של ברנש מוזר. גם חתימתו בתור "הטייל" הוציאה לו שם של שוטה, שכן המילה משמשת גם לשוטים.
אך הוא עצמו עסק במתמטיקה מורכבת במיוחד. בהמשך חייו הוא אכן תרם למתמטיקה ולמדע את תרומתו האדירה, כשזיהה את "סדרת פיבונאצ'י", סדרת מספרים מופלאה שכל מספר הוא סכום הקודמים לו.
הצגת הסדרה וההגיון שבה פתחו פתח לזיהוי היחסים המדהימים שבין יופיים של הטבע והאמנות לבין הסדר המתמטי המדהים שבהם, סדר שהוגדר על ידי רבים כלא פחות מאשר "הפרופורציה האלוהית" (ראו באאוריקה בתגית "סדרת פיבונאצ'י"). בפשטות נאמר שזוהי סדרת מספרים שאם נחלק כל מספר בה במספר שקדם לו, נלך ונתקרב למספר 1.618. זהו המספר הידוע במתמטיקה, מאז היוונים הקדמונים, בתור "פיי" ("Phi"). אנו קוראים לו יחס הזהב והיוונים קשרו אותו אל היופי המושלם.
פיבונאצ'י הסביר שבמיני פרחים שונים ובאיצטרובלים - לאן שהביט הוא גילה בטבע את הצורות של הסדרה המתמטית שהציג. הוא גם זיהה את "מלבן הזהב" שנמצא בזרעי החמניות, בקונכיות, שבלולים, בצמחים סוקולנטיים, מיצירות אמנות ועד גלקסיות חלזוניות. חוקרים רבים אחריו גילו עד כמה נמצאים סדרת פיבונאצ'י ויחס הזהב בכל מקום.
כיום נחשב פיבונאצ'י בעיני רבים לגדול המתמטיקאים של ימי הביניים.
הנה סיפורו של פיבונאצי והסדרה המתמטית המופלאה שמצא (עברית):
https://youtu.be/EAXKR-H_bS0?t=8s
סרטון על לאונרדו פיבונצ'י:
http://youtu.be/wTlw7fNcO-0
הסבר לסדרת פיבונצ'י (מתורגם):
http://youtu.be/z5RWfXTd3QU
וסרט תיעודי על לאונרדו פיבונצ'י:
https://youtu.be/O2wU-HT7FiM?long=yes
מהי הפרופורציה האלוהית?
זה קרה בשנת 1202 כשמתמטיקאי קדום ורב זכויות סיפר את סיפור הארנבים, שמולידים צאצא אחד בכל חודש ומתרבים בקצב לוגריתמי. הוא הציג לעולם סדרת מספרים שסכום כל שני מספרים עוקבים בה יהיה המספר הבא. אבל הסדרה הזו צפנה סודות נוספים ומדהימים. תוכלו ללמוד עליהם לעומק באאוריקה, בתגית "סדרת פיבונאצ'י".
אבל המעניין הוא שכמעט מבלי משים חשף פיבונאצ'י בתגלית שלו את אחד מסודות האסתטיקה המעניינים בהיסטוריה. הוא גילה שיופי ומתמטיקה הלכו במשך אלפי שנים יד ביד, כשאמנים, אדריכלים ויוצרים מכל הזמנים אחזו בתפיסת יופי ואסתטיקה דומים, מבלי לתאם זאת ביניהם.
ועוד יותר, הוא זיהה שהתפיסה הזו טבעית ומשותפת לכל בני האדם, בלי הבדל של תרבות, מקום וזמן. בכל כיוון שאליו נפנה מבט, נוכל לראות את אצבע אלוהים, או לפחות את מודל היופי שהוא יצר בטבע ושבאופן בלתי תלוי אימצו כל התרבויות העתיקות. מקונכיות וחלזונות, דרך פרחים ואיצטרובלים ועד לגלקסיות שלמות - הטבע מוצף ביחס הזהב שגילה פיבונאצ'י.
מסתבר שהמתמטיקה גילתה את הדרך היעילה ביותר לשכפול של תאים ולתנועה בחלל וזו, אם תרצו, יצרה פרופורציה שכולה אצבע אלוהים.
הנה הפרופורציה האלוהית שהלכה והתגלתה מאז פיבונאצ'י:
http://youtu.be/03uC9bhX0Rc
הדוגמאות הרבות של הפרופורציה האלוהית בעולם:
http://youtu.be/0hvD5kLqjuw
קבלו נסיון לבחון את המונה ליזה וכיצד יצר לאונרדו, כמו אמנים רבים, תמונה עם פרופורציות מושלמות שלמד מהטבע:
http://youtu.be/JFTSAjZEqPw
הסבר של הפרופורציה האלוהית וטענה די מוזרה שמסתירים אותה מהציבור:
http://youtu.be/4VrcO6JaMrM
וסרטון תיעודי על המתמטיקה המופלאה של פיבונאצ'י שמייצרת את היופי הזה:
https://youtu.be/keLN89CWZ-A?long=yes
זה קרה בשנת 1202 כשמתמטיקאי קדום ורב זכויות סיפר את סיפור הארנבים, שמולידים צאצא אחד בכל חודש ומתרבים בקצב לוגריתמי. הוא הציג לעולם סדרת מספרים שסכום כל שני מספרים עוקבים בה יהיה המספר הבא. אבל הסדרה הזו צפנה סודות נוספים ומדהימים. תוכלו ללמוד עליהם לעומק באאוריקה, בתגית "סדרת פיבונאצ'י".
אבל המעניין הוא שכמעט מבלי משים חשף פיבונאצ'י בתגלית שלו את אחד מסודות האסתטיקה המעניינים בהיסטוריה. הוא גילה שיופי ומתמטיקה הלכו במשך אלפי שנים יד ביד, כשאמנים, אדריכלים ויוצרים מכל הזמנים אחזו בתפיסת יופי ואסתטיקה דומים, מבלי לתאם זאת ביניהם.
ועוד יותר, הוא זיהה שהתפיסה הזו טבעית ומשותפת לכל בני האדם, בלי הבדל של תרבות, מקום וזמן. בכל כיוון שאליו נפנה מבט, נוכל לראות את אצבע אלוהים, או לפחות את מודל היופי שהוא יצר בטבע ושבאופן בלתי תלוי אימצו כל התרבויות העתיקות. מקונכיות וחלזונות, דרך פרחים ואיצטרובלים ועד לגלקסיות שלמות - הטבע מוצף ביחס הזהב שגילה פיבונאצ'י.
מסתבר שהמתמטיקה גילתה את הדרך היעילה ביותר לשכפול של תאים ולתנועה בחלל וזו, אם תרצו, יצרה פרופורציה שכולה אצבע אלוהים.
הנה הפרופורציה האלוהית שהלכה והתגלתה מאז פיבונאצ'י:
http://youtu.be/03uC9bhX0Rc
הדוגמאות הרבות של הפרופורציה האלוהית בעולם:
http://youtu.be/0hvD5kLqjuw
קבלו נסיון לבחון את המונה ליזה וכיצד יצר לאונרדו, כמו אמנים רבים, תמונה עם פרופורציות מושלמות שלמד מהטבע:
http://youtu.be/JFTSAjZEqPw
הסבר של הפרופורציה האלוהית וטענה די מוזרה שמסתירים אותה מהציבור:
http://youtu.be/4VrcO6JaMrM
וסרטון תיעודי על המתמטיקה המופלאה של פיבונאצ'י שמייצרת את היופי הזה:
https://youtu.be/keLN89CWZ-A?long=yes
איך נוצרים הגרעינים השחורים?
הם הפיצוחים הכי אהובים אצלנו. כשרואים משחק כדורגל או כדורסל בטלוויזיה הם כמעט מצרך חובה ויש אנשים רבים שאין אצלם סוף שבוע בלי לפצח גרעינים ובמיוחד את השחורים שבהם הוא לא סופ"ש. אולי סוף.
אז הגרעינים הלבנים הם גרעיני דלעת וגרעיני אבטיח באים מזרעי האבטיח, אבל מאיפה מגיעים הגרעינים השחורים?
הגרעינים השחורים הם גרעיני חמנית. קוטפים אותם בקיץ, בשעה מסוימת מאוד, בה הם נקטפים בקלות. בעבר קטפו אותם בידיים, אבל כיום קוצר אותם הקומביין הענק בשדה החמניות והם ייאגרו בו, עד שיועברו בשקים אל בית הקלייה.
בבית הקליה יקלו את כל סוגי הגרעינים - מהגרעינים השחורים, דרך גרעיני אבטיח וכמובן גרעינים לבנים, שבאים מהדלעת.
בבית הקליה, לאחר מכן, יארזו את הגרעינים האפויים בשקיות והם יישלחו לחנויות.
גרעיני החמנייה הם שהופכים לגרעינים שחורים (עברית):
https://youtu.be/xLCkC0oOFqw
גרעיני חמניה היו תמיד זולים וסיפקו בילוי נחמד והיו מי שהתפרנסו מהם היטב (עברית):
https://youtu.be/zRXRdRvz-3U
שיר שמדגים כמה הגרעינים מרכזיים בהוויה הישראלית (עברית):
https://youtu.be/WdWIFqhhwCs
והגרעינים הם חלק מהפיצוחים שאנו כה אוהבים (עברית):
https://youtu.be/zNfOKCcyK0g
הם הפיצוחים הכי אהובים אצלנו. כשרואים משחק כדורגל או כדורסל בטלוויזיה הם כמעט מצרך חובה ויש אנשים רבים שאין אצלם סוף שבוע בלי לפצח גרעינים ובמיוחד את השחורים שבהם הוא לא סופ"ש. אולי סוף.
אז הגרעינים הלבנים הם גרעיני דלעת וגרעיני אבטיח באים מזרעי האבטיח, אבל מאיפה מגיעים הגרעינים השחורים?
הגרעינים השחורים הם גרעיני חמנית. קוטפים אותם בקיץ, בשעה מסוימת מאוד, בה הם נקטפים בקלות. בעבר קטפו אותם בידיים, אבל כיום קוצר אותם הקומביין הענק בשדה החמניות והם ייאגרו בו, עד שיועברו בשקים אל בית הקלייה.
בבית הקליה יקלו את כל סוגי הגרעינים - מהגרעינים השחורים, דרך גרעיני אבטיח וכמובן גרעינים לבנים, שבאים מהדלעת.
בבית הקליה, לאחר מכן, יארזו את הגרעינים האפויים בשקיות והם יישלחו לחנויות.
גרעיני החמנייה הם שהופכים לגרעינים שחורים (עברית):
https://youtu.be/xLCkC0oOFqw
גרעיני חמניה היו תמיד זולים וסיפקו בילוי נחמד והיו מי שהתפרנסו מהם היטב (עברית):
https://youtu.be/zRXRdRvz-3U
שיר שמדגים כמה הגרעינים מרכזיים בהוויה הישראלית (עברית):
https://youtu.be/WdWIFqhhwCs
והגרעינים הם חלק מהפיצוחים שאנו כה אוהבים (עברית):
https://youtu.be/zNfOKCcyK0g
מה מיוחד במוזיאון גוגנהיים?
מוזיאון גוגנהיים בעיר ניו-יורק תוכנן על ידי האדריכל הידוע פרנק לויד רייט. רייט נדרש ל-700 שרטוטים ול-15 שנה עד שהצליח להגיע למה שרצה - מבנה שיהיה שונה מכל "הקופסאות" שמסביב.
ואכן, המבנה של מוזיאון גוגנהיים בניו-יורק הוא בעל צורה ייחודית שרבים מחשיבים כיצירת אמנות לא פחות חשובה מהיצירות המופשטות שמוצגות בו. הצורה המעוגלת, הלא סימטרית, הבלתי סדירה ושחלקה הרחב הוא דווקא למעלה היא בלתי נשכחת. הוא גם היה המוזיאון הראשון שבו הגלריה היא אחת - אין קומות ואין חדרים, אלא רק חלל אחד המתעקל בשיפוע מתון במורד המבנה, למלמעלה ועד לקומת הכניסה.
מה שאפשר את הקסם הזה, הוא התכנון של המבנה לפי סדרת פיבונאצ'י ועל פי יחס הזהב. ממש כמו קונכיית הנאוטילוס, הקונכייה הכי קדומה שעדיין קיימת בעולם ולא השתנתה מאז ימי הדינוזאורים.
את הרעיון קיבל האדריכל לאחר שהברונית העשירה מזמינת העבודה דרשה שהמבנה יהיה מעוגל. מכאן הדרך הייתה קצרה לחיקוי של קונכיית הנאוטילוס, שכולו מחושב על בסיס עיקרון פיבונאצ'י (ראו בתגית "סדרת פיבונאצ'י"). זהו עיקרון שמבוסס על חתך הזהב (ראו בתגית "יחס הזהב"), הצורה היעילה ביותר בטבע לשכפול מוקטן.
הנה סרטון של מוזיאון גוגנהיים:
https://youtu.be/QvgVKWvb2tI
שיטוט בחלל הפנימי של המוזיאון:
https://youtu.be/ypDTotRZPgY
הזמנה להגיע אליו:
https://youtu.be/OmAaZmACy20
והמבנה המיוחד של גוגנהיים והמודלים ששימשו בזמן התכנון:
https://youtu.be/O_YzxQecZMs
מוזיאון גוגנהיים בעיר ניו-יורק תוכנן על ידי האדריכל הידוע פרנק לויד רייט. רייט נדרש ל-700 שרטוטים ול-15 שנה עד שהצליח להגיע למה שרצה - מבנה שיהיה שונה מכל "הקופסאות" שמסביב.
ואכן, המבנה של מוזיאון גוגנהיים בניו-יורק הוא בעל צורה ייחודית שרבים מחשיבים כיצירת אמנות לא פחות חשובה מהיצירות המופשטות שמוצגות בו. הצורה המעוגלת, הלא סימטרית, הבלתי סדירה ושחלקה הרחב הוא דווקא למעלה היא בלתי נשכחת. הוא גם היה המוזיאון הראשון שבו הגלריה היא אחת - אין קומות ואין חדרים, אלא רק חלל אחד המתעקל בשיפוע מתון במורד המבנה, למלמעלה ועד לקומת הכניסה.
מה שאפשר את הקסם הזה, הוא התכנון של המבנה לפי סדרת פיבונאצ'י ועל פי יחס הזהב. ממש כמו קונכיית הנאוטילוס, הקונכייה הכי קדומה שעדיין קיימת בעולם ולא השתנתה מאז ימי הדינוזאורים.
את הרעיון קיבל האדריכל לאחר שהברונית העשירה מזמינת העבודה דרשה שהמבנה יהיה מעוגל. מכאן הדרך הייתה קצרה לחיקוי של קונכיית הנאוטילוס, שכולו מחושב על בסיס עיקרון פיבונאצ'י (ראו בתגית "סדרת פיבונאצ'י"). זהו עיקרון שמבוסס על חתך הזהב (ראו בתגית "יחס הזהב"), הצורה היעילה ביותר בטבע לשכפול מוקטן.
הנה סרטון של מוזיאון גוגנהיים:
https://youtu.be/QvgVKWvb2tI
שיטוט בחלל הפנימי של המוזיאון:
https://youtu.be/ypDTotRZPgY
הזמנה להגיע אליו:
https://youtu.be/OmAaZmACy20
והמבנה המיוחד של גוגנהיים והמודלים ששימשו בזמן התכנון:
https://youtu.be/O_YzxQecZMs
מה זה לוליין לוגריתמי?
לוליין לוגריתמי, ספירלה לוגריתמית, או ספירלת הזהב, הם שמות של אחת התופעות המרהיבות בטבע. מדובר בצורה גיאומטרית, של קו עקום ומעגלי המתחיל מנקודה כלשהי ומסתחרר בצורה מעגלית כלפי חוץ, כשהרדיוס של המעגל הולך וגדל, כמו חילזון (ספירלה).
צורה זו היא מעין צורה בסיסית של יופי. היא כוללת סימטריה והרמוניה - שתי התכונות שגורמות לבני אדם לזהות דבר יפה, כבר ממבט ראשון. כבר דורות מתואר הלוליין הלוגריתמי בתור "הפרופורציה האלוהית". כזו שיכולה להקנות לדברים שהאדם עושה את תכונות היופי הכי מוכרות, סימטריה והרמוניה.
שתי התוכנות הללו מתמזגות בלוליין הלוגריתמי. בזכותו הופכים הפרחים, למשל, ליפים בעינינו, כמו גם בעיני בעלי חיים. בזכות היופי ההרמוני והסימטריה המושלמת נמשכים אליהם הדבורים, הפרפרים והחרקים ומוצאים בהם מקור למזון וחיים.
השלמות והיופי הללו, של מה שקיבל את השם "יחס הזהב", גלומים בכל פינה בטבע. מפרחים כמו חמנית או ורד, פירות דוגמת אננס, ירקות כמו הכרוב והכרובית, צמחים כמו ברוקולי ואצל בעלי חיים כמו במראה קרני האיילים, פרפרים, שבלולים, קונכיות וחלזונות - כולם מתפתחים כך. גם בתופעות טבע כמו מערבולות מים ואוויר ואפילו גלקסיות עם מיליארדי כוכבים. כל אלה נראים כך. הסיבה היא שהאנרגיה הדרושה לכל אלה היא המינימלית. גדילה כזו של יצורים חיים, או קיומן של תופעות כמו מערבולת או אפילו גלקסיה, תובעות אנרגיה רבה. לכן חסכון טבעי בה הוא הכי טוב.
התופעות הללו משכו את תשומת לב האמנים ומתכנני המבנים, שכן יופיים לא משתנה והם נחשבים יפים בכל תקופה ובכל תרבות שהן. מקרני האיילים שהיו לקורות עמודים רומיים, אזור המפתחות בכלי המיתר ועד ללוליינים לוגריתמיים שהיו לכלי אמנותי בציור ובעיצוב והאדריכלות של מוזיאון גוגנהיים.
בצמחים ופרפרים רבים, גם כשהתכונות הללו לא נראות במבט ראשון, אפשר לדמיין את הצורה הלוליינית ומיד מזהים את ההרמוניה והסימטריה שהעין כה אוהבת.
הנה הספירלה של הלוליין הלוגריתמי שמופיעה בטבע בכל מקום:
https://youtu.be/nt2OlMAJj6o
ספירלת הזהב על פי פיבונאצ'י, היא הלוליין הלוגריתמי:
https://youtu.be/RKdrI9MZXHQ
תיאור של לוליין לוגריתמי בעזרת תוכנה מתמטית:
https://youtu.be/gXU1D2aF8QI
ומצגת וידאו של מרכיבים לולייניים שונים בטבע:
https://youtu.be/Qq7nU62ww0U
לוליין לוגריתמי, ספירלה לוגריתמית, או ספירלת הזהב, הם שמות של אחת התופעות המרהיבות בטבע. מדובר בצורה גיאומטרית, של קו עקום ומעגלי המתחיל מנקודה כלשהי ומסתחרר בצורה מעגלית כלפי חוץ, כשהרדיוס של המעגל הולך וגדל, כמו חילזון (ספירלה).
צורה זו היא מעין צורה בסיסית של יופי. היא כוללת סימטריה והרמוניה - שתי התכונות שגורמות לבני אדם לזהות דבר יפה, כבר ממבט ראשון. כבר דורות מתואר הלוליין הלוגריתמי בתור "הפרופורציה האלוהית". כזו שיכולה להקנות לדברים שהאדם עושה את תכונות היופי הכי מוכרות, סימטריה והרמוניה.
שתי התוכנות הללו מתמזגות בלוליין הלוגריתמי. בזכותו הופכים הפרחים, למשל, ליפים בעינינו, כמו גם בעיני בעלי חיים. בזכות היופי ההרמוני והסימטריה המושלמת נמשכים אליהם הדבורים, הפרפרים והחרקים ומוצאים בהם מקור למזון וחיים.
השלמות והיופי הללו, של מה שקיבל את השם "יחס הזהב", גלומים בכל פינה בטבע. מפרחים כמו חמנית או ורד, פירות דוגמת אננס, ירקות כמו הכרוב והכרובית, צמחים כמו ברוקולי ואצל בעלי חיים כמו במראה קרני האיילים, פרפרים, שבלולים, קונכיות וחלזונות - כולם מתפתחים כך. גם בתופעות טבע כמו מערבולות מים ואוויר ואפילו גלקסיות עם מיליארדי כוכבים. כל אלה נראים כך. הסיבה היא שהאנרגיה הדרושה לכל אלה היא המינימלית. גדילה כזו של יצורים חיים, או קיומן של תופעות כמו מערבולת או אפילו גלקסיה, תובעות אנרגיה רבה. לכן חסכון טבעי בה הוא הכי טוב.
התופעות הללו משכו את תשומת לב האמנים ומתכנני המבנים, שכן יופיים לא משתנה והם נחשבים יפים בכל תקופה ובכל תרבות שהן. מקרני האיילים שהיו לקורות עמודים רומיים, אזור המפתחות בכלי המיתר ועד ללוליינים לוגריתמיים שהיו לכלי אמנותי בציור ובעיצוב והאדריכלות של מוזיאון גוגנהיים.
בצמחים ופרפרים רבים, גם כשהתכונות הללו לא נראות במבט ראשון, אפשר לדמיין את הצורה הלוליינית ומיד מזהים את ההרמוניה והסימטריה שהעין כה אוהבת.
הנה הספירלה של הלוליין הלוגריתמי שמופיעה בטבע בכל מקום:
https://youtu.be/nt2OlMAJj6o
ספירלת הזהב על פי פיבונאצ'י, היא הלוליין הלוגריתמי:
https://youtu.be/RKdrI9MZXHQ
תיאור של לוליין לוגריתמי בעזרת תוכנה מתמטית:
https://youtu.be/gXU1D2aF8QI
ומצגת וידאו של מרכיבים לולייניים שונים בטבע:
https://youtu.be/Qq7nU62ww0U
מהי סדרת פיבונאצ'י?
סדרת פיבונאצ'י במתמטיקה היא סדרת מספרים שהאיברים הראשונים בה הם 1 ו-1. כל איבר אחר בסדרת פיבונאצ'י שווה לסכום של שני האיברים הקודמים לו. 2 שווה ל-1 ועוד 1, 3 שווה 2+1, 5 הוא 2+3 וכן הלאה.
הסדרה קרויה על שם המתמטיקאי לאונרדו דה פיזה (לאונרדו מהעיר פיזה) שבאיטליה, שכונה "פיבונאצ'י". פיבונאצ'י תיאר את הסדרה הזו ב"ספר החשבוניה" שיצא בשנת 1202. הוא השתמש בסדרת פיבונאצ'י כדי לתאר את מספר הצאצאים של זוג ארנבים אחד. הוא תאר מצב שכל זוג ארנבים מגיל חודשיים ומעלה, ממליט מדי חודש זוג נוסף, התוצאות של מספר הצאצאים שלהם יהיו על פי הסדרה הזו.
מסתבר שהיחס בין שני איברים עוקבים של מספרי פיבונאצ'י שואף ל"יחס הזהב", קבוע מתמטי שתואר כבר ביוון העתיקה. תמיד כשמחלקים שני איברים עוקבים בסדרת פיבונאצ'י, התוצאה תלך ותתקרב לחתך הזהב. בדרך זו מוסברים דברים רבים בטבע בעזרת סדרת פיבונאצ'י והרקורסיה (ראו באאוריקה בתגית "מה זה, רקורסיה"), מקונכיות עם "ספירלת הזהב", דרך פרחים, כרובית, גלקסיות חלזוניות ועוד. וזה לא במקרה שסדרת פיבונאצ'י היא כה נפוצה בטבע - כמו שהראינו קודם בדוגמת הארנבים, מדובר בצורה היעילה ביותר לשכפול וכשצמחים ובעלי חיים פשוטים משכפלים תאים בגדילה - מקבלים בדיוק את הסדרה של פיבונאצ'י.
מקובל לסמן את איברי הסדרה באות F, שמוגדרת ברקורסיה - כלומר פעולה המבוצעת על ידי הפניה עצמית. במקרה הזה, כל F הוא סכום שני ה-Fים שלפניו.
הנה הסבר על סדרת פיבונאצ'י (עברית):
https://youtu.be/EAXKR-H_bS0
הסבר מדעי של הסדרה הפיבונאצ'ית (עברית):
http://youtu.be/z5RWfXTd3QU
הדגמה של סדרת פיבונאצ'י:
http://youtu.be/H2aHh5FLX5w
והסבר מתמטי של סדרת ה פיבונאצ'י (מתורגם):
https://youtu.be/SjSHVDfXHQ4
סדרת פיבונאצ'י במתמטיקה היא סדרת מספרים שהאיברים הראשונים בה הם 1 ו-1. כל איבר אחר בסדרת פיבונאצ'י שווה לסכום של שני האיברים הקודמים לו. 2 שווה ל-1 ועוד 1, 3 שווה 2+1, 5 הוא 2+3 וכן הלאה.
הסדרה קרויה על שם המתמטיקאי לאונרדו דה פיזה (לאונרדו מהעיר פיזה) שבאיטליה, שכונה "פיבונאצ'י". פיבונאצ'י תיאר את הסדרה הזו ב"ספר החשבוניה" שיצא בשנת 1202. הוא השתמש בסדרת פיבונאצ'י כדי לתאר את מספר הצאצאים של זוג ארנבים אחד. הוא תאר מצב שכל זוג ארנבים מגיל חודשיים ומעלה, ממליט מדי חודש זוג נוסף, התוצאות של מספר הצאצאים שלהם יהיו על פי הסדרה הזו.
מסתבר שהיחס בין שני איברים עוקבים של מספרי פיבונאצ'י שואף ל"יחס הזהב", קבוע מתמטי שתואר כבר ביוון העתיקה. תמיד כשמחלקים שני איברים עוקבים בסדרת פיבונאצ'י, התוצאה תלך ותתקרב לחתך הזהב. בדרך זו מוסברים דברים רבים בטבע בעזרת סדרת פיבונאצ'י והרקורסיה (ראו באאוריקה בתגית "מה זה, רקורסיה"), מקונכיות עם "ספירלת הזהב", דרך פרחים, כרובית, גלקסיות חלזוניות ועוד. וזה לא במקרה שסדרת פיבונאצ'י היא כה נפוצה בטבע - כמו שהראינו קודם בדוגמת הארנבים, מדובר בצורה היעילה ביותר לשכפול וכשצמחים ובעלי חיים פשוטים משכפלים תאים בגדילה - מקבלים בדיוק את הסדרה של פיבונאצ'י.
מקובל לסמן את איברי הסדרה באות F, שמוגדרת ברקורסיה - כלומר פעולה המבוצעת על ידי הפניה עצמית. במקרה הזה, כל F הוא סכום שני ה-Fים שלפניו.
הנה הסבר על סדרת פיבונאצ'י (עברית):
https://youtu.be/EAXKR-H_bS0
הסבר מדעי של הסדרה הפיבונאצ'ית (עברית):
http://youtu.be/z5RWfXTd3QU
הדגמה של סדרת פיבונאצ'י:
http://youtu.be/H2aHh5FLX5w
והסבר מתמטי של סדרת ה פיבונאצ'י (מתורגם):
https://youtu.be/SjSHVDfXHQ4
מהו האדם הוויטרובי של לאונרדו דה וינצ'י?
האדם הוויטרובי הוא אולי הרישום המפורסם ביותר של האמן לאונרדו דה וינצ'י. הרישום, שנקרא גם "קאנון היחסים", צוייר בשנת 1490 ומתאר דרך הפרופורציות והסימטריה של הגוף האנושי את השלמות וההרמוניה שראו מדעני ואמני התקופה. בראש אותם המגלים עמד לאונרדו עצמו - אולי החוקר, היוצר, המהנדס והממציא החשוב בתולדות האנושות.
הרישום הזה של לאונרדו נחשב מיצירות האמנות המוכרות ואף החשובות של הרנסאנס האיטלקי. מהות התקופה הייתה הגילוי מחדש של חוקים אמנותיים, אסתטיים ומדעיים, שהיו ידועים בתרבויות העבר הרומיות, היווניות ואלה שלפניהן.
חלק מהפלאים שהתגלו שוב ברנסאנס היו קשורים ביחסים המתמטיים המדוייקים שבטבע. לאונרדו רשם את "האדם הוויטרובי" לאחר שעיין בפרופורציות גוף האדם שצויינו בספרו של האדריכל הרומאי ויטרוביוס "על אודות האדריכלות".
הנה הסבר מתורגם על האדם הוויטרובי של לאונרדו דה וינצ'י (מתורגם):
http://youtu.be/aMsaFP3kgqQ?t=14s
בשנות ה-80 השתמשה האוניברסיטה הפתוחה באדם הוויטרובי כפתיח לשידורי הטלוויזיה שלה:
https://youtu.be/I1ZVjfUaz9M
ניסיון "לשדרג" את האדם הוויטרובי למאה ה-21:
http://youtu.be/jwnTvv7NaJA
וסרט תיעודי על האדם הויטרובי:
https://youtu.be/GGUOtwDhyzc?long=yes
האדם הוויטרובי הוא אולי הרישום המפורסם ביותר של האמן לאונרדו דה וינצ'י. הרישום, שנקרא גם "קאנון היחסים", צוייר בשנת 1490 ומתאר דרך הפרופורציות והסימטריה של הגוף האנושי את השלמות וההרמוניה שראו מדעני ואמני התקופה. בראש אותם המגלים עמד לאונרדו עצמו - אולי החוקר, היוצר, המהנדס והממציא החשוב בתולדות האנושות.
הרישום הזה של לאונרדו נחשב מיצירות האמנות המוכרות ואף החשובות של הרנסאנס האיטלקי. מהות התקופה הייתה הגילוי מחדש של חוקים אמנותיים, אסתטיים ומדעיים, שהיו ידועים בתרבויות העבר הרומיות, היווניות ואלה שלפניהן.
חלק מהפלאים שהתגלו שוב ברנסאנס היו קשורים ביחסים המתמטיים המדוייקים שבטבע. לאונרדו רשם את "האדם הוויטרובי" לאחר שעיין בפרופורציות גוף האדם שצויינו בספרו של האדריכל הרומאי ויטרוביוס "על אודות האדריכלות".
הנה הסבר מתורגם על האדם הוויטרובי של לאונרדו דה וינצ'י (מתורגם):
http://youtu.be/aMsaFP3kgqQ?t=14s
בשנות ה-80 השתמשה האוניברסיטה הפתוחה באדם הוויטרובי כפתיח לשידורי הטלוויזיה שלה:
https://youtu.be/I1ZVjfUaz9M
ניסיון "לשדרג" את האדם הוויטרובי למאה ה-21:
http://youtu.be/jwnTvv7NaJA
וסרט תיעודי על האדם הויטרובי:
https://youtu.be/GGUOtwDhyzc?long=yes
מהי קונכיית הנאוטילוס העתיקה?
הנאוטילוס הוא מעין דיונון בעל קונכייה שיש לו כמה זרועות ציד קצרות. לקונכיית הנאוטילוס פסים בצבעי אדום ולבן. יש לו סיבה טובה להיות גאה בעצמו, שכן הוא מבעלי החיים היחידים ששרדו ללא שינוי מאז ימי הדינוזאורים ומהרכיכות היחידות ששרדו מתקופת המזוזואיקון. המבנה האורגני של הנאוטילוס לא השתנה במשך 400 מיליון שנה. לכן הנאוטילוס מוגדר כמאובן חי, מה שאומר שהיצורים הקרובים אליה נכחדו וקשה יותר למצוא יצורים כאלה שחיים, מאשר מאובנים של יצורים שנכחדו.
הנאוטילוס הוא קרוב משפחה של האמוניט הקדום, מתקופת המזוזואיקון. אבל בעוד שהאמוניט נכחד בהכחדה הגדולה שחיסלה גם את הדינוזאורים, לפני 65 מליון שנה, הצליח הנאוטילוס לשרוד את האירועים שהכחידו מינים רבים כל כך, מהאמוניטים ועד הדינוזאורים.
קונכיית הנאוטילוס היא דוגמה חלזונית שמדגימה את יחס הזהב בטבע (ראו בתגית "יחס הזהב") והיא בנויה על פי סדרת פיבונאצ'י.
הסופר הבדיוני הראשון והמפורסם ז'ול ורן קרא על שמה את הצוללת "נאוטילוס" מספרו "20,000 מיל מתחת לפני הים". בהמשך ההיסטוריה נשאו כמה צוללות אמיתיות את השם, כגון הצוללת שניסתה לחצות תחת הקוטב בשנת 1931 והצוללת הגרעינית הראשונה של הצבא האמריקאי.
הנה קונכיית הנאוטילוס:
http://youtu.be/HIRCI0G19Uw
המחקר עליה:
http://youtu.be/PIheRYcm6sI
נאוטילוס טורף:
https://youtu.be/vR6G-ANma1w
הנאוטילוס הוא אחת הדוגמאות הטבעיות הטובות של חתך הזהב:
https://youtu.be/_gxC8OjoQkQ
והתנועה האצילית של הנאוטילוס במים, כשבניגוד למנהגו הוא עולה ממעמקים אל פני הים:
https://youtu.be/dHqvQ8WBFeM
הנאוטילוס הוא מעין דיונון בעל קונכייה שיש לו כמה זרועות ציד קצרות. לקונכיית הנאוטילוס פסים בצבעי אדום ולבן. יש לו סיבה טובה להיות גאה בעצמו, שכן הוא מבעלי החיים היחידים ששרדו ללא שינוי מאז ימי הדינוזאורים ומהרכיכות היחידות ששרדו מתקופת המזוזואיקון. המבנה האורגני של הנאוטילוס לא השתנה במשך 400 מיליון שנה. לכן הנאוטילוס מוגדר כמאובן חי, מה שאומר שהיצורים הקרובים אליה נכחדו וקשה יותר למצוא יצורים כאלה שחיים, מאשר מאובנים של יצורים שנכחדו.
הנאוטילוס הוא קרוב משפחה של האמוניט הקדום, מתקופת המזוזואיקון. אבל בעוד שהאמוניט נכחד בהכחדה הגדולה שחיסלה גם את הדינוזאורים, לפני 65 מליון שנה, הצליח הנאוטילוס לשרוד את האירועים שהכחידו מינים רבים כל כך, מהאמוניטים ועד הדינוזאורים.
קונכיית הנאוטילוס היא דוגמה חלזונית שמדגימה את יחס הזהב בטבע (ראו בתגית "יחס הזהב") והיא בנויה על פי סדרת פיבונאצ'י.
הסופר הבדיוני הראשון והמפורסם ז'ול ורן קרא על שמה את הצוללת "נאוטילוס" מספרו "20,000 מיל מתחת לפני הים". בהמשך ההיסטוריה נשאו כמה צוללות אמיתיות את השם, כגון הצוללת שניסתה לחצות תחת הקוטב בשנת 1931 והצוללת הגרעינית הראשונה של הצבא האמריקאי.
הנה קונכיית הנאוטילוס:
http://youtu.be/HIRCI0G19Uw
המחקר עליה:
http://youtu.be/PIheRYcm6sI
נאוטילוס טורף:
https://youtu.be/vR6G-ANma1w
הנאוטילוס הוא אחת הדוגמאות הטבעיות הטובות של חתך הזהב:
https://youtu.be/_gxC8OjoQkQ
והתנועה האצילית של הנאוטילוס במים, כשבניגוד למנהגו הוא עולה ממעמקים אל פני הים:
https://youtu.be/dHqvQ8WBFeM
למה אקרופוליס נמצא מעל העיר?
האקרופוליס (Acropolis) הייתה גבעה מבוצרת בערים יווניות בתקופה העתיקה, שבה נמצא בדרך כלל ארמון המלך והמקדשים של העיר.
האקרופוליס הידועה ביותר היא האקרופוליס באתונה. השריד המפורסם באקרופוליס של אתונה הוא "הפרתנון", מקדש יווני עתיק שהפך לסמל של יוון העתיקה ולדוגמה לאקרופוליס היווני הנישא מעל העיר. אקרופוליס מוכרים אחרים יש בערי-מדינה יווניות עתיקות אחרות כמו ארגוס, תביי וקורינתוס.
על אף אי הדיוק שבכך, כיום מכנים "אקרופוליס" כל גבעה מבוצרת שנמצאת בעיר עתיקה, בלי קשר לתקופה, בין אם מדובר בתקופת יוון העתיקה ובין אם לא. כך למשל מכונות הגבעות המבוצרות של אימפריית המאיה.
אקרופוליס פירושו ביוונית "מעל העיר" או העיר העליונה.
הנה אתונה והאקרופוליס שבראשה:
https://youtu.be/dJlNDgo1GJE
כך נבנה הפרתנון באתונה (מתורגם):
https://youtu.be/tuZcS2Flabw
בואו לבקר באקרופוליס של העיר ארגוס:
http://youtu.be/RpDqaNE93bo
הסבר על האקרופוליס המפורסם ביותר שנותר מיוון העתיקה:
http://youtu.be/xP-FsX0QW88
המראה של אתונה מהאקרופוליס שמעליה:
http://youtu.be/AdisSwq90Lk
מבט מלמעלה על האקרופוליס והפרתנון:
http://youtu.be/MsfUR_jTAKU
האקרופוליס באתונה הומה תיירים:
http://youtu.be/uS85O9KzGSo
וסרט תלת-ממדי על האקרופוליס היווני:
http://youtu.be/kEaepiwK1KM?3d=yes
האקרופוליס (Acropolis) הייתה גבעה מבוצרת בערים יווניות בתקופה העתיקה, שבה נמצא בדרך כלל ארמון המלך והמקדשים של העיר.
האקרופוליס הידועה ביותר היא האקרופוליס באתונה. השריד המפורסם באקרופוליס של אתונה הוא "הפרתנון", מקדש יווני עתיק שהפך לסמל של יוון העתיקה ולדוגמה לאקרופוליס היווני הנישא מעל העיר. אקרופוליס מוכרים אחרים יש בערי-מדינה יווניות עתיקות אחרות כמו ארגוס, תביי וקורינתוס.
על אף אי הדיוק שבכך, כיום מכנים "אקרופוליס" כל גבעה מבוצרת שנמצאת בעיר עתיקה, בלי קשר לתקופה, בין אם מדובר בתקופת יוון העתיקה ובין אם לא. כך למשל מכונות הגבעות המבוצרות של אימפריית המאיה.
אקרופוליס פירושו ביוונית "מעל העיר" או העיר העליונה.
הנה אתונה והאקרופוליס שבראשה:
https://youtu.be/dJlNDgo1GJE
כך נבנה הפרתנון באתונה (מתורגם):
https://youtu.be/tuZcS2Flabw
בואו לבקר באקרופוליס של העיר ארגוס:
http://youtu.be/RpDqaNE93bo
הסבר על האקרופוליס המפורסם ביותר שנותר מיוון העתיקה:
http://youtu.be/xP-FsX0QW88
המראה של אתונה מהאקרופוליס שמעליה:
http://youtu.be/AdisSwq90Lk
מבט מלמעלה על האקרופוליס והפרתנון:
http://youtu.be/MsfUR_jTAKU
האקרופוליס באתונה הומה תיירים:
http://youtu.be/uS85O9KzGSo
וסרט תלת-ממדי על האקרופוליס היווני:
http://youtu.be/kEaepiwK1KM?3d=yes
מהו הפרתנון שבאקרופוליס של אתונה?
"הפרתנון" (Parthenon) הוא השריד העיקרי של אתונה העתיקה. הוא נמצא באקרופוליס של אתונה העתיקה, גבעה הניצבת "מעל העיר" (זה הפירוש ביוונית של אקרופוליס). חוץ מהפרתנון יש באקרופוליס של אתונה שרידים נוספים של מבנים חשובים.
הפרתנון הוא מקדש שנבנה במקום בו ניצב קודם מקדש עתיק יותר והפרסים הרסו אותו במלחמה. הפרתנון נבנה במאה ה-5 לפני הספירה כאות תודה לאלה אתנה, הפטרונית של העיר אתונה, על שנתנה את הניצחון ליוונים במלחמתם נגד פרס.
כמו מבנים עתיקים רבים בעולם העתיק ויצירות אמנות יפות לאורך ההיסטוריה, גם הפרתנון בנוי בפרופורציות של "מלבן הזהב", על פי חוקיות האסתטיקה חוצה התקופות הידועה כ"הפרופורציה האלוהית". ראו באאוריקה בתגית "יחס הזהב".
כאמור, האקרופוליס פירושו ביוונית: העיר העליונה. זוהי גבעה מבוצרת בעיר-מדינה ביוון העתיקה. לרוב שכן באקרופוליס ארמון המלך ובהמשך ההיסטוריה נמצאו בו כמעט תמיד המצודה והמקדשים של העיר. קראו על המושג באאוריקה בתגית "אקרופוליס".
יצרים, אגו וגאונות - מה שליווה את בניית הפרתנון המפורסם של אתונה (מתורגם):
https://youtu.be/tuZcS2Flabw
הפרתנון של אתונה - באקרופוליס שמעל העיר:
https://youtu.be/xP-FsX0QW88
מבט מהאוויר של אתונה והאקרופוליס שבראשה:
https://youtu.be/dJlNDgo1GJE
אולי הוא נראה פעם כך:
https://youtu.be/s8OblzGTxYE
עוד מהאקרופוליס באתונה:
http://youtu.be/cu9osYLbY3g
סיור וירטואלי בפרתנון המדהים שבאתונה:
http://youtu.be/CjQYFizc2B8
כך נראה אולי הפרתנון באקרופוליס של אתונה:
https://youtu.be/ASdYVEIDXnM
והפרתנון העתיק קם לתחייה בתלת-ממד:
https://youtu.be/G1D5hbxa8CM
"הפרתנון" (Parthenon) הוא השריד העיקרי של אתונה העתיקה. הוא נמצא באקרופוליס של אתונה העתיקה, גבעה הניצבת "מעל העיר" (זה הפירוש ביוונית של אקרופוליס). חוץ מהפרתנון יש באקרופוליס של אתונה שרידים נוספים של מבנים חשובים.
הפרתנון הוא מקדש שנבנה במקום בו ניצב קודם מקדש עתיק יותר והפרסים הרסו אותו במלחמה. הפרתנון נבנה במאה ה-5 לפני הספירה כאות תודה לאלה אתנה, הפטרונית של העיר אתונה, על שנתנה את הניצחון ליוונים במלחמתם נגד פרס.
כמו מבנים עתיקים רבים בעולם העתיק ויצירות אמנות יפות לאורך ההיסטוריה, גם הפרתנון בנוי בפרופורציות של "מלבן הזהב", על פי חוקיות האסתטיקה חוצה התקופות הידועה כ"הפרופורציה האלוהית". ראו באאוריקה בתגית "יחס הזהב".
כאמור, האקרופוליס פירושו ביוונית: העיר העליונה. זוהי גבעה מבוצרת בעיר-מדינה ביוון העתיקה. לרוב שכן באקרופוליס ארמון המלך ובהמשך ההיסטוריה נמצאו בו כמעט תמיד המצודה והמקדשים של העיר. קראו על המושג באאוריקה בתגית "אקרופוליס".
יצרים, אגו וגאונות - מה שליווה את בניית הפרתנון המפורסם של אתונה (מתורגם):
https://youtu.be/tuZcS2Flabw
הפרתנון של אתונה - באקרופוליס שמעל העיר:
https://youtu.be/xP-FsX0QW88
מבט מהאוויר של אתונה והאקרופוליס שבראשה:
https://youtu.be/dJlNDgo1GJE
אולי הוא נראה פעם כך:
https://youtu.be/s8OblzGTxYE
עוד מהאקרופוליס באתונה:
http://youtu.be/cu9osYLbY3g
סיור וירטואלי בפרתנון המדהים שבאתונה:
http://youtu.be/CjQYFizc2B8
כך נראה אולי הפרתנון באקרופוליס של אתונה:
https://youtu.be/ASdYVEIDXnM
והפרתנון העתיק קם לתחייה בתלת-ממד:
https://youtu.be/G1D5hbxa8CM
מהו פאי?
הפאי הוא מספר אי רציונאלי, מציין את היחס בין היקף מעגל לקוטרו. זהו מספר מסתורי, שמתמטיקאים וחובבי מתמטיקה מוקסמים ממנו כבר דורות רבים. ערכו של פאי שווה בקירוב ל 3.14.
הפאי מסומן באות היוונית π. הבבלים, ממציאי הגלגל, גילו אותו כבר לפני ששת אלפים שנה. התגלית של התופעה המרתקת של פאי, הייתה שבכל גודל מעגל שהוא, תוצאת החילוק של היקף המעגל ברדיוס שלו תהיה תמיד אותו המספר. 4000 שנה אחריהם, הצליחו מדעני מצרים העתיקה להגיע לערך מקורב של פאי. ארכימדס היווני הציג לראשונה, כבר במאה ה-3 לפני הספירה, שיטה שמאפשרת לאמוד את π.
הראשון שהצליח לחשב את פיי בדיוק גבוה היה אויילר. פיתוח החשבון הדיפרנציאלי והאינטגרלי סייע לו מאד והוא חישב את פאי עד 153 ספרות אחרי הנקודה. כמו הרבה דברים שאויילר תרם למתמטיקה, הוא גם זה שהעניק לפיי את שמו.
כיום, בעידן המחשב, המתמטיקאים עובדים על אלגוריתמים ונוסחאות אלגנטיות לחישוב פאי. השיא שנקבע עד 2011 הוא של 10 טריליון ספרות אחרי הנקודה!
הנה סרטון על משמעותו של הפיי (מתורגם):
http://youtu.be/9a5vHXsUvUw?t=13s
שיר לימודי באנגלית, להיכרות עם חישוב פאי:
http://youtu.be/eiHWHT_8WrE
מלחין שהחליט להלחין את המספר וכך לזכור אותו:
https://youtu.be/wM-x3pUcdeo
והביטוי המוסיקלי של המספר פאי ויחס הזהב שבנוי עליו:
https://youtu.be/9mozmHgg9Sk?long=yes
הפאי הוא מספר אי רציונאלי, מציין את היחס בין היקף מעגל לקוטרו. זהו מספר מסתורי, שמתמטיקאים וחובבי מתמטיקה מוקסמים ממנו כבר דורות רבים. ערכו של פאי שווה בקירוב ל 3.14.
הפאי מסומן באות היוונית π. הבבלים, ממציאי הגלגל, גילו אותו כבר לפני ששת אלפים שנה. התגלית של התופעה המרתקת של פאי, הייתה שבכל גודל מעגל שהוא, תוצאת החילוק של היקף המעגל ברדיוס שלו תהיה תמיד אותו המספר. 4000 שנה אחריהם, הצליחו מדעני מצרים העתיקה להגיע לערך מקורב של פאי. ארכימדס היווני הציג לראשונה, כבר במאה ה-3 לפני הספירה, שיטה שמאפשרת לאמוד את π.
הראשון שהצליח לחשב את פיי בדיוק גבוה היה אויילר. פיתוח החשבון הדיפרנציאלי והאינטגרלי סייע לו מאד והוא חישב את פאי עד 153 ספרות אחרי הנקודה. כמו הרבה דברים שאויילר תרם למתמטיקה, הוא גם זה שהעניק לפיי את שמו.
כיום, בעידן המחשב, המתמטיקאים עובדים על אלגוריתמים ונוסחאות אלגנטיות לחישוב פאי. השיא שנקבע עד 2011 הוא של 10 טריליון ספרות אחרי הנקודה!
הנה סרטון על משמעותו של הפיי (מתורגם):
http://youtu.be/9a5vHXsUvUw?t=13s
שיר לימודי באנגלית, להיכרות עם חישוב פאי:
http://youtu.be/eiHWHT_8WrE
מלחין שהחליט להלחין את המספר וכך לזכור אותו:
https://youtu.be/wM-x3pUcdeo
והביטוי המוסיקלי של המספר פאי ויחס הזהב שבנוי עליו:
https://youtu.be/9mozmHgg9Sk?long=yes
מה זו סופת הטורנדו ואיך טורנדו נוצר?
סופת טורנדו היא סופה בצורת מערבולת, שעוברת ממקום למקום ויכולה להיות מאד הרסנית. על אף שרוחב סופת הטורנדו הוא רק כמה מאות מטרים, היא הורסת מבנים ושואבת אליה חפצים גדולים כמו גגות ומכוניות, שלעיתים מוצאים אותם לאחר הסופה במרחק רב ממקומם. מהירות הרוח של סופת טורנדו מגיעה ל-100 קילומטרים בשעה! כוח היניקה שלה למעלה, גורם לנזקים גדולים בנפש וברכוש.
הטורנדו נוצר מרוח חזקה שפוגעת בעננים ומחוללת עם האוויר החם העולה מהקרקע את צורת המשפך. סופת הטורנדו נושאת אבק ואדי מים ונראית כמשפך צר שיורד מחלקו התחתון של ענן אל עבר הקרקע.
סופת טורנדו נוצרת לרוב במהירות רבה ולכן קשה מאד להתריע עליה ולפנות את האזורים שאליהם היא עומדת להגיע מאנשים.
מרבית סופות הטורנדו בעולם מתרחשות באזור ארצות הברית.
סופות טורנדו הן אחד המקרים שבו ניתן לראות את היחס המתמטי המופלא של "חיתוך הזהב" (או "יחס הזהב"). את היחס המופלא הזה, שזכה גם לשם "הפרופורציה האלוהית", ניתן למצוא בטבע אצל חלזונות וקונכיות, מערבולות, סופות טורנדו וגלקסיות ספירליות, אך גם באמנות, מוסיקה ובאדריכליות. קראו עליו באאוריקה בתגית "חתך הזהב".
הנה הסבר יפה ומתורגם על סופות הטורנדו והיווצרותן (מתורגם):
http://youtu.be/lmWh9jV_1ac
כך נולדת סופת טורנדו בגודל בלתי נתפס:
https://youtu.be/2pnz3dwq9aE
דוגמה להיווצרות של טורנדו:
http://youtu.be/7KDz6dGQ5RE
הסבר לילדים על הדרך שבה נוצרת סופת הטורנדו:
http://youtu.be/FbXvj1mgPdA
כך נוצרות סופות טורנדו וכמה מהסופות בהיסטוריה:
http://youtu.be/S-UPAcKNvII
סופת טורנדו בזמן אמת:
https://youtu.be/xPTXqzMVFUA
מעט מההרס שיכול להיגרם מסופת טורנדו:
http://youtu.be/43VoMesUd2Q
והסבר על הטורנדו ודרך היווצרותו (עברית):
https://youtu.be/XMlPZ-CmTh0?long=yes
סופת טורנדו היא סופה בצורת מערבולת, שעוברת ממקום למקום ויכולה להיות מאד הרסנית. על אף שרוחב סופת הטורנדו הוא רק כמה מאות מטרים, היא הורסת מבנים ושואבת אליה חפצים גדולים כמו גגות ומכוניות, שלעיתים מוצאים אותם לאחר הסופה במרחק רב ממקומם. מהירות הרוח של סופת טורנדו מגיעה ל-100 קילומטרים בשעה! כוח היניקה שלה למעלה, גורם לנזקים גדולים בנפש וברכוש.
הטורנדו נוצר מרוח חזקה שפוגעת בעננים ומחוללת עם האוויר החם העולה מהקרקע את צורת המשפך. סופת הטורנדו נושאת אבק ואדי מים ונראית כמשפך צר שיורד מחלקו התחתון של ענן אל עבר הקרקע.
סופת טורנדו נוצרת לרוב במהירות רבה ולכן קשה מאד להתריע עליה ולפנות את האזורים שאליהם היא עומדת להגיע מאנשים.
מרבית סופות הטורנדו בעולם מתרחשות באזור ארצות הברית.
סופות טורנדו הן אחד המקרים שבו ניתן לראות את היחס המתמטי המופלא של "חיתוך הזהב" (או "יחס הזהב"). את היחס המופלא הזה, שזכה גם לשם "הפרופורציה האלוהית", ניתן למצוא בטבע אצל חלזונות וקונכיות, מערבולות, סופות טורנדו וגלקסיות ספירליות, אך גם באמנות, מוסיקה ובאדריכליות. קראו עליו באאוריקה בתגית "חתך הזהב".
הנה הסבר יפה ומתורגם על סופות הטורנדו והיווצרותן (מתורגם):
http://youtu.be/lmWh9jV_1ac
כך נולדת סופת טורנדו בגודל בלתי נתפס:
https://youtu.be/2pnz3dwq9aE
דוגמה להיווצרות של טורנדו:
http://youtu.be/7KDz6dGQ5RE
הסבר לילדים על הדרך שבה נוצרת סופת הטורנדו:
http://youtu.be/FbXvj1mgPdA
כך נוצרות סופות טורנדו וכמה מהסופות בהיסטוריה:
http://youtu.be/S-UPAcKNvII
סופת טורנדו בזמן אמת:
https://youtu.be/xPTXqzMVFUA
מעט מההרס שיכול להיגרם מסופת טורנדו:
http://youtu.be/43VoMesUd2Q
והסבר על הטורנדו ודרך היווצרותו (עברית):
https://youtu.be/XMlPZ-CmTh0?long=yes
