שלום,
נראה שכבר הכרתם את אאוריקה. בטח כבר גיליתם כאן דברים מדהימים, אולי כבר שאלתם שאלות וקיבלתם תשובות טובות.
נשמח לראות משהו מכם בספר האורחים שלנו: איזו מילה טובה, חוות דעת, עצה חכמה לשיפור או כל מה שיש לכם לספר לנו על אאוריקה, כפי שאתם חווים אותה.
»
«
 מהי סטטיסטיקה?
מהי סטטיסטיקה?
סטטיסטיקה היא תחום ידע שבו אוספים ומנתחים מידע כמותי, כדי להסיק מסקנות. כך למשל אוספים נתונים על אזרחי המדינה ומנתחים אותם וכך לומדים על חייהם, עיסוקיהם, מצבם הכלכלי ועוד. או שאוספים את נתוני הקליעה של שחקני כדורסל ואחרי ניתוח מגיעים למסקנות על הבולטים שבהם ואלו שעושים עבודה פחות טובה.
הסטטיסטיקה נחשבת מדע שאינו ניסויי, אך היא משרתת היטב את אנשי המדע. הסטטיסטיקאים משתמשים בכלים מתמטיים כדי לטפל בנתונים שלקוחים במרבית המקרים מהתחומים המדעיים של מדעי הטבע ומדעי החברה ומסייעים לגלות בהם דברים חשובים, שיכולים לתרום מאד.
אך לסטטיסטיקה יש גם מגבלות לא קטנות. למשל בכך שהיא עובדת טוב על מספרים גדולים ודי רע על מספרים קטנים. לדוגמה, הבה נביט על אדם שרגלו האחת בגיגית מים רותחים ורגלו השנייה בגיגית של מים קפואים. על פי הסטטיסטיקה יהיה מצבו טוב, שכן ממוצע החום שבין המים הרותחים והמים הקפואים יהיה נורמלי. עם זאת, ברור לנו שבמציאות אדם כזה יסבול מאד... אולי משום כך היה מי שהעיד שאמר פעם בנג'מין ד'יזראלי, ראש ממשלת בריטניה, "יש שלושה סוגי שקרים: שקרים, שקרים גסים וסטטיסטיקה"...
דוגמה נוספת לבעיה של הסטטיסטיקה היא היכולת לנבא ממדגם קטן על האוכלוסיה כולה. למשל, לא פעם חוזים הסוקרים הפוליטיים את תוצאות הבחירות. הם עושים זאת בעזרת מדגם (קבוצה קטנה שאמורה לייצג את האוכלוסיה כולה). אך לא פעם, עם פרסום תוצאות האמת, מסתבר שהם טעו. ברוב המקרים הסיבה לכך היא שסטטיסטיקה היא מנבא מוגבל ולא תמיד מדויק של המציאות.
הנה דוגמאות קטנות למסקנות מעולם הסטטיסטיקה (עברית):
https://youtu.be/o4oM-7UOYRQ
סרטון שמדגים כמה שסטטיסטיקה יכולה להטעות כשמבינים ממנה דברים לא נכונים (עברית):
http://youtu.be/cKHAfiqHwZc
הסבירות הגדולה שסטטיסטיקה תטעה (מתורגם):
https://youtu.be/sxYrzzy3cq8
והסטודנטים לסטטיסטיקה באוניברסיטה (עברית):
https://youtu.be/b-k13rnRFcU
 מהן השפות שהכי הרבה אנשים מדברים בהן?
מהן השפות שהכי הרבה אנשים מדברים בהן?
יש בעולם מעל 6500 שפות שונות.
מביניהן, השפות הכי מדוברות בעולם הן סינית, אנגלית, ספרדית, ערבית ורוסית. כמות האנשים שמדברים שפות אלה היא הגדולה ביותר מכל שפה אחרת.
סין היא המדינה בעלת האוכלוסיה הגדולה בעולם ולכן הסינית היא השפה שמספרית הכי הרבה מדברים בה.
מנגד, הפכה השפה האנגלית במאה ה-20 לשפה הבינלאומית המנצחת ולכן רוב אזרחי העולם שמדברים שפה נוספת מדברים בה.
כך התפתחו שפות העולם (מתורגם):
http://youtu.be/iWDKsHm6gTA
 מהי רגרסיה לממוצע?
מהי רגרסיה לממוצע?
למה סרטי המשך של להיטים קולנועיים לא יצליחו כמו הסרט הראשון?
איך זה שילדיהם של גאונים או כשרונות גדולים לא יהיו מוצלחים כמוהם?
למה ספורטאי לא ישבור ברצף שיאים?
האם ראיתם או קרה פעם משהו מדהים וחשבתם שהוא יקרה שוב, אבל הוא לא חזר על עצמו בפעם הבאה? - ובכן, זה נורמלי וזו תופעה ידועה בשם "תסוגה לממוצע" או רגרסיה לממוצע.
רגרסיה לממוצע היא תופעה מרתקת וטבעית, שמתגלית שוב ושוב בתחומים רבים, הן בטבע והן במעשים ידי אדם.
התופעה אומרת שהסבירות של התרחשויות קיצוניות ברצף, זו אחרי זו, היא נמוכה מאד. כלומר, אחרי התרחשות של אירוע קיצוני כלשהו, אם יש קשר חיובי בין ההתרחשויות (מה שנקרא במדע "מתאם סטטיסטי חיובי"), כמעט בוודאות לא יהיה האירוע הבא מסוגו כה קיצוני והוא יהיה קרוב יותר לממוצע.
מי שגילה את התופעה ופרסם אותה בסוף המאה ה-19 היה המדען האנגלי סר פרנסיס גולטון, מי שגילה את המתאם הסטטיסטי וגם אחראי לגילוי עקרון "חוכמת ההמונים". גולטון חקר את הרגרסיה לממוצע בזרעים ובגבהים של הורים וילדים והופתע לגלות כמה התופעה רווחת וכמה היא יכולה להיות שימושית לניבוי דברים כמו מגמות עתידיות בתחומים רבים, או שינויים במצבם של חולים.
הנה הסבר על התסוגה לממוצע:
https://youtu.be/GEmuEWjHr5c
והסבר מילולי של הרגרסיה לממוצע:
https://youtu.be/Qw8b_igoMTM
 מהי הסתברות?
מהי הסתברות?
אי-ודאות היא אחד הדברים שמלווים אותנו בחיים. לא פעם אנו חשים בחוסר וודאות, מכיוון שאין לנו יכולת לחזות את מזג האוויר, תוצאות של אירועי ספורט, או תוצאות של בחירות. למצבים כאלו יש כלי שיכול לסייע - הִסְתַּבְּרוּת (Probability).
הסתברות היא מושג מתמטי שמבטא את הסבירות שמאורע מסוים יתרחש. לעיתים יש לנו מושג מה סביר שיקרה, גם אם איננו יודעים בודאות מה יקרה. תורת ההסתברות מכמתת את "הסביר" ומודדת אותו באופן מדויק.
מדידת הסתברות של מאורע מסוים היא בסקאלה שבין 0 ל־1. מאורע בלתי אפשרי מקבל הסתברות 0, בעוד הסתברות 1 ניתנת למאורע שיש ודאות מוחלטת שיקרה. לעיתים קורה שמשתמשים באחוזים, בין 0% ל־100%, כדי לבטא הסתברות.
כשאנו מטילים מטבע, ההסתברות שהוא יפול על צד מסוים שלו היא 0.5, כלומר שבממוצע המטבע תיפול על אותו צד באחת מכל שתי זריקות. באופן דומה, ההסתברות שהכדור ברולטה ייפול על כל אחד מהמספרים, היא שווה.
היסטורית יש להסתברות עבר ארוך. עוד במאה ה-16 עסקו בחישובי הסתברויות. מאז הלך הענף הזה במתמטיקה והתפתח, כשהשימוש בו מסייע בתחומי הכלכלה, העסקים, ההימורים ועוד.
כך למשל קובעות חברות ביטוח את מחיר ביטוח החיים על פי ההסתברות שהמבוטח ייפגע או ימות במהלך תקופת הביטוח. חזאי מזג אוויר בוחנים את ההסתברות לגשם, בכדי להציע תחזית אמינה.
גם מהמרים נעזרים בחישובים כדי לדעת את הסיכויים שיזכו בהגרלות או במשחקים וכך הלאה.
הנה הדרך שבה ניתן לראות הסתברות (מתורגם):
https://youtu.be/Kgudt4PXs28
הדגמת ההסתברות דרך ניחושים (מתורגם):
https://youtu.be/3V2omKRX9gc
בעיית מונטי הול מדגימה יפה את ההסתברות וכמה שאינה אינטואיטיבית (עברית):
https://youtu.be/4stFDiXWuYk
מה ההסתברות לזכות בפיס כלומר בלוטו (עברית)?
https://youtu.be/_vyjrgU7hng
ודוגמה להסתברות שנוגדת את האינטואיציה שלנו (מתורגם):
https://youtu.be/Ghbkv0MKV-w
 מה הקשר בין קופים לגאונות?
מה הקשר בין קופים לגאונות?
משפט הקוף המקליד גורס שבסופה של הקלדת כל רצף ארוך מספיק של תווים אקראיים, יופיע כמעט בוודאות, כל טקסט אפשרי. התאוריה אומרת שאם תהיה ההקלדה אינסופית, יווצר בוודאות כל טקסט שהוא, כולל נבואות, טקסטים של שייקספיר ורשימות מכולת מאתמול. זהו סדר שנוצר מתוך כאוס.
מתמטיקאי צרפתי בשם אמיל בורל היה הראשון שכתב את הדברים. הוא ניסח זאת כך שניתן לומר שאם קוף יקליד תווים אקראיים במכונת כתיבה, לבסוף הוא יקליד גם את כל כתבי וויליאם שייקספיר.
בגישה זו ניתן לענות גם לטענה שנבואות קדומות ניבאו כל מיני אירועים שקרו במאה האחרונה (כולל עלית היטלר, רצח רבין ועוד). הם גורסים בפשטות שבתנ"ך ניתן למצוא "רמזים" לאירועים אלה ואחרים, אם רק מחפשים מספיק...
אבל מה ניתן להפיק מהקלדות אקראיות כמו מה שהקופים מקלידים? - משפט הקוף המקליד הוא ניסוי מחשבתי בלבד. בניסוי שערכו ב-2003 בגן חיות, הסתבר שקופי המקוק שקיבלו 6 מכונות כתיבה למשך חודש כתבו רק 5 עמודים, שרובם היו מלאים באות "S" והרסו את מכונות הכתיבה.
אתר שמדמה את הקופים המקלידים בעזרת תוכנה שיוצרת אינספור הקלדות אקראיות, הצליח להפיק 24 אותיות רצופות מתוך המחזה "הנרי הרביעי" של שייקספיר.
על תיאורמת הקוף האינסופי, או משפט הקוף המקליד (ללא מילים):
http://youtu.be/Imd_Vhg8Afk?t=13s
תיאור ציורי של תיאורת הקופים האינסופיים:
http://youtu.be/ipdRhgLWGXo
על תוצאותיו של הניסוי עם קופים ומכונות כתיבה:
http://youtu.be/pDUn7dDigvI
וסימולטור שמדמה את תיאורמת הקופים האינסופיים:
http://youtu.be/iSn8L6Uj5L8
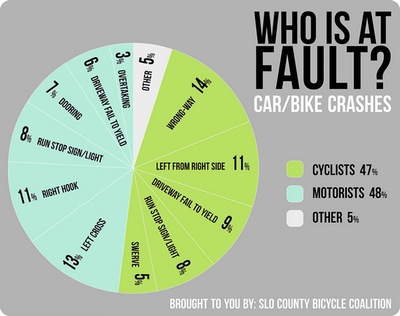
 למה משתמשים באינפוגרפיקה?
למה משתמשים באינפוגרפיקה?
ויזואליות עובדת הרבה יותר טוב מרשימות ארוכות של טקסט. זה ידוע כבר שנים רבות.
אינפוגרפיקה (Infographic) היא המחשת מידע (הדגמה) בעזרת אמצעים גרפיים מגוונים, כמו איורים, תמונות, אנימציה, גרפים, תרשימי זרימה ועוד.
שיטת האינפוגרפיקה משמשת להצגה פשוטה ומובנת יותר של תהליכים שונים, מידע מורכב וכבד, רצף אירועים וכדומה. המבוגרים, שאוהבים מילים קשות ומרשימות בלועזית, היו אומרים שהאינפוגרפיקה היא סוג של ויזואליזציה (המחשה ויזואלית) המלווה בהסברים טקסטואליים.
לתחום האינפוגרפיקה יש שורשים עתיקים, שמגיעים עד התרבות של סין העתיקה. בעידן המודרני נחשב פרופסור בשם אדוארד טאפטי לאבי האינפוגרפיקה היישומית המודרנית.
בשנים האחרונות הולכת האינפוגרפיקה ונעשית פופולארית. שילוב אינפוגראפיקה באינטרנט, ובמאמרים בעיתונות הפך נפוץ ושכיח מאד.
כולנו הרי יודעים שפעמים רבות היכולת של איור או צילום להמחיש רעיון מורכב או לסייע ביצירתיות וחשיבה יצירתית, היא טובה הרבה יותר מפסקאות ארוכות של מלל. כבר מזמן אמרו הרי הסבים והסבתות שלנו ש"תמונה טובה מאלף מילים".
הנה הסבר המושג אינפוגרפיקה:
https://youtu.be/M3fBmZR2fTU
באנימציה:
https://youtu.be/zbTYyl7WVd8
שימוש באינפוגרפיקה לסרטון הדרכה:
https://youtu.be/VCG_L5jEX0c
וכך מציגים מדינה באמצעות אינפוגרפיקה:
https://youtu.be/i9vzQJylSFg
או תפוח:
https://youtu.be/rzRZPAnJU1Q
 למה משתמשים בגרף בועות?
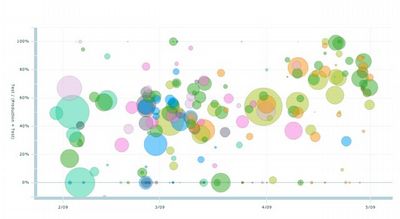
למה משתמשים בגרף בועות?
גרף בועות (Bubble Chart) דומה לגרף פיזור בכך שהוא מציג נקודות במערכת צירים עבור שני משתנים, אך מוסיף את גודל הנקודה כמידע נוסף. למעשה, כל "בועה" בגרף היא נקודה שהשטח שלה (או הרדיוס שלה) משקפת משתנה שלישי.
כך ניתן לדוגמה לבנות גרף בועות שבו כל בועה היא מדינה בעולם: מיקום אופקי מייצג בו את התוצר לנפש במדינה, מיקום אנכי מייצג את תוחלת החיים וגודל הבועה מייצג את גודל האוכלוסייה. כך נראה בבת אחת את הקשר בין עושר לאריכות חיים וגם אילו מדינות הן גדולות באוכלוסייה - מדינות עם הרבה תושבים יהיו בועות גדולות ומדינות קטנות יהיו בועות קטנות.
כלומר, באמצעות גרף כזה אפשר להעביר בהצגה דו-ממדית שלושה ממדי מידע: מיקום אופקי (X), מיקום אנכי (Y) וגודל (Z) שניתן לראות באמצעות גודל הבועה.
ואגב, לפעמים משתמשים גם בצבע הבועות כדי לשקף משתנה רביעי, אבל לרוב שני צירים וגודל נותנים כבר תמונה עשירה.
#יתרונות
גרף בועות מאפשר להציג יותר מידע באותה תמונה. הוא מצטיין בהמחשת מערכות נתונים מורכבות שבהן שני משתנים לא מספרים את כל הסיפור. הבועות מוסיפות ממד חדש, אך מבלי לעבור לגרף תלת-ממדי שהוא שקשה יותר לקריאה.
היתרון הוא שניתן לזהות דפוסים שאולי היו נסתרים אם היו מציגים כל פעם רק שני משתנים. אפשר לראות שלושה משתנים קשורים. במקרה המדינות, למשל, ייתכן שנגלה שמדינות עם תוצר גבוה ותוחלת חיים גבוהה הן גם בעלות אוכלוסייה בינונית, ואילו מדינות עם אוכלוסייה עצומה הן לאו דווקא הכי עשירות.
#התאמה
גרף בועות מתאים במיוחד למצבים שבהם יש שלושה משתנים כמותיים לכל פריט ונרצה לבדוק את היחסים ביניהם. הרבה פעמים משתמשים בזה בכלכלה וחברה - למשל להצגת נתוני המדינות כפי שתואר (עושר, בריאות, גודל אוכלוסייה) או להשוואת ביצועי חברות עסקיות (ציר אחד יכול להיות רווח, ציר שני צמיחה וגודל הבועה הוא שווי השוק של החברה).
גם בשיווק אפשר להשתמש בגרף עם בועות. למשל, כשכל בועה היא מוצר. עם ציר X למחיר, ציר Y לשביעות רצון לקוחות וגודל הבועה עבור כמות המכירות. כך ניתן להבין היכן ממוקמים המוצרים בשוק ביחס לשביעות הרצון מהם מול מחירם.
#דוגמאות
בדוגמה אמיתית הוצג על-ידי הנס רוסלינג (Hans Rosling) גרף בועות מפורסם ובו הוא תיאר את התפתחות מדינות העולם. באותו גרף ראו על גבי הגרף בועה לכל מדינה. הציר האופקי היה ההכנסה, הציר האנכי תוחלת החיים, בעוד שגודל הבועה ייצג את גודל האוכלוסייה. כך ניתן היה לראות בקלות את הודו וסין עם אוכלוסיותיהם העצומות, כבועות גדולות ועולות בציר ההכנסה לאורך השנים.
דוגמה יומיומית יותר היא של חנות מקוונת שיכולה לנתח את מוצריה בעזרת גרף בועות. כל בועה מייצגת עבורה מוצר. המיקום האופקי בגרף מייצג את מחירו והמיקום האנכי את דירוג הלקוחות (בכוכבים למשל), בעוד גודל הבועה מייצג את כמות המכירות של אותו מוצר. מבט כזה יכול לגלות שאין קשר בין המחיר לדירוג, אבל כן רואים שמוצרים עם דירוג גבוה נמכרים יותר. זה ייראה בבירור כשבועות גדולות מרוכזות באזורי הדירוג הגבוה בגרף.
הנה הסבר של גרף הבועות:
https://youtu.be/iv0CT5H0yug
עשו ואל תעשו בגרף בועות:
https://youtu.be/Fygi3mQY0Ag
ודוגמאות לגרף בועות בתוכנת Excel:
https://youtu.be/Q1uiytD86OQ
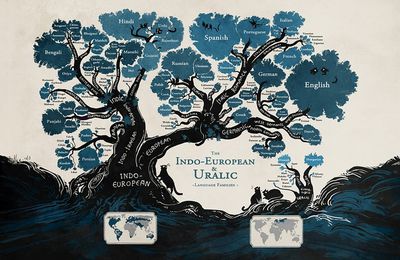 כמה שפות מדוברות יש בעולם?
כמה שפות מדוברות יש בעולם?
בעולם יש כ-6500 שפות מדוברות. ביניהן יש גם כ-120 שפות סימנים לחרשים וסובלים מליקויי שמיעה.
חשוב לדעת, עם זאת, ש-2000 מתוך השפות שיש בעולם, מדוברות על ידי פחות מ-1000 איש. לרוב מדובר על שפות של שבטים קטנים המוגדרות כשפות בסכנת הכחדה.
השפה הסינית מנדרינית היא המדוברת ביותר בעולם. מעריכים שמעל מיליארד ו-200 מיליון איש מדברים בה, אם כי יש מקורות המציינים מספרים שונים.
הנה סרטון קצרצר על השפות הפופולריות בעולם:
https://youtu.be/GxrtddcYEwM
וכך נוצרו כל כך הרבה שפות בעולם לא גדול כמו שלנו (מתורגם):
https://youtu.be/iWDKsHm6gTA
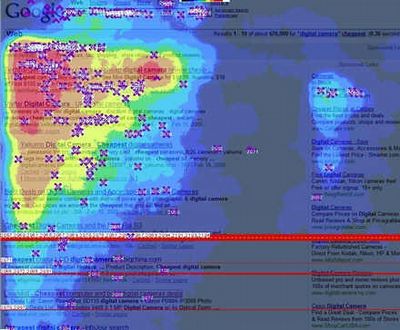 מה מציגה מפת חום?
מה מציגה מפת חום?
מפת חום (Heatmap) מציגה טבלה של ערכים בשני ממדים כאשר הערכים מיוצגים כצבעים.
כלומר, יש לנו ציר אופקי וציר אנכי (למשל, ימים ושעות, או פריטים שונים מול תכונות שונות), ובנקודת המפגש של כל שני פרמטרים יש ערך מספרי שמיוצג על ידי צבע.
במפת חום לרוב משתמשים בסקאלה צבעונית. למשל, מכחול דרך צהוב עד אדום, כדי לציין מערך ערכים נמוכים עד גבוהים.
היתרון הוא שבמבט אחד ניתן לאתר דפוסים: אזורים חמים (בצבע בולט כמו אדום) לעומת קרים (כחול או צבע כהה) שמראים איפה הערכים גבוהים או נמוכים במיוחד.
לדוגמה, דמיינו heatmap שבו ניתן לראות את עומס המבקרים בחנות לאורך הימים והשעות. כל שורה מייצגת יום בשבוע וכל עמודה שעה ביום. בעוד הצבע הלבן-צהוב מצביע על שעות שיא עם הרבה לקוחות (צהרי היום ובערב), השחור-אדמדם מצביע על שעות שקטות (למשל באמצע הלילה או מוקדם בבוקר).
כך ניתן לראות במבט מהיר שבסופי שבוע (שבת-ראשון) בצהריים יש צבע בהיר מאוד, כלומר החנות עמוסה אז במיוחד.
#יתרונות
מפת חום מצטיינת ביכולת להראות הרבה מידע בתמונה אחת באופן אינטואיטיבי. היא טובה בזיהוי תבניות, כי העין שלנו מיד נמשכת לאזורים בולטים בצבעם. למשל, אם נשתמש במפת חום להצגת ציוני תלמידים במקצועות שונים (שורות תלמידים, עמודות מקצועות, וצבע = ציון), נוכל מיד להבחין באילו מקצועות כיתה שלמה חזקה (מה שייראה בצורת עמודה בולטת בצבע מסוים) או האם תלמיד ספציפי בולט לרעה או לטובה (שורה מסוימת עם צבעים קיצוניים).
#התאמה
מפת החום מתאימה במיוחד עבור נתונים בעלי שני ממדים של קטגוריות או רצף, כשעבור כל צירוף שלהם יש ערך מספרי.
זה יכול להיות זמנים מול מקומות (כמו בדוגמת החנות: לכל יום ושעה יש מספר של לקוחות), או אנשים מול תכונות (למשל, טבלת תלמידים וציוניהם בכמה מקצועות), או אפילו מטריצה של מתאם בין משתנים (כשרוצים לראות אילו משתנים קשורים, עם ערכים גבוהים בצבע בולט).
מפת חום שימושית גם למדעני נתונים בתחומים כמו ביולוגיה ובינה מלאכותית, כדי להציג מטריצות גדולות בצורה שקל לקלוט (כמו "DNA Microarray" בביולוגיה, שמציג ביטויי גנים שונים כדוגמאות צבע).
#דוגמאות
דוגמה מהחיים: רשת חברתית יכולה להציג למנהלי הקהילה מפה צבעונית של פעילות המשתמשים לפי שעה ויום: למשל, הצבעים יראו שבשעות הערב של סוף השבוע הפעילות באתר בשיאה (צבע חם מאוד) ואילו בשעות בוקר של אמצע השבוע הפעילות נמוכה (צבע קר).
דוגמה נוספת: אפליקציית תחבורה ציבורית עשויה להראות Heatmap של עומס נוסעים בתחנות שונות לאורך היום. כך ניתן לראות באילו תחנות ושעות יש עומס גדול (אדום), מה שעוזר בהקצאת משאבים כמו אוטובוסים נוספים בזמן הנכון.
מהי מפת חום?
https://youtu.be/Q3XFj3zJBuE
מפת חום בגוגל Sheet:
https://youtu.be/RuvbI3QcsFo
ליצור מפת חום בתוכנת אקסל:
https://youtu.be/4Ftu8ay4UKc
הרצאונת על מהי מפת חום ואיך להשתמש בה:
https://youtu.be/stgf2CfiXr4
ומפת חום מורכבת במיוחד:
https://youtu.be/NFbiSX6PYXo

סטטיסטיקה היא תחום ידע שבו אוספים ומנתחים מידע כמותי, כדי להסיק מסקנות. כך למשל אוספים נתונים על אזרחי המדינה ומנתחים אותם וכך לומדים על חייהם, עיסוקיהם, מצבם הכלכלי ועוד. או שאוספים את נתוני הקליעה של שחקני כדורסל ואחרי ניתוח מגיעים למסקנות על הבולטים שבהם ואלו שעושים עבודה פחות טובה.
הסטטיסטיקה נחשבת מדע שאינו ניסויי, אך היא משרתת היטב את אנשי המדע. הסטטיסטיקאים משתמשים בכלים מתמטיים כדי לטפל בנתונים שלקוחים במרבית המקרים מהתחומים המדעיים של מדעי הטבע ומדעי החברה ומסייעים לגלות בהם דברים חשובים, שיכולים לתרום מאד.
אך לסטטיסטיקה יש גם מגבלות לא קטנות. למשל בכך שהיא עובדת טוב על מספרים גדולים ודי רע על מספרים קטנים. לדוגמה, הבה נביט על אדם שרגלו האחת בגיגית מים רותחים ורגלו השנייה בגיגית של מים קפואים. על פי הסטטיסטיקה יהיה מצבו טוב, שכן ממוצע החום שבין המים הרותחים והמים הקפואים יהיה נורמלי. עם זאת, ברור לנו שבמציאות אדם כזה יסבול מאד... אולי משום כך היה מי שהעיד שאמר פעם בנג'מין ד'יזראלי, ראש ממשלת בריטניה, "יש שלושה סוגי שקרים: שקרים, שקרים גסים וסטטיסטיקה"...
דוגמה נוספת לבעיה של הסטטיסטיקה היא היכולת לנבא ממדגם קטן על האוכלוסיה כולה. למשל, לא פעם חוזים הסוקרים הפוליטיים את תוצאות הבחירות. הם עושים זאת בעזרת מדגם (קבוצה קטנה שאמורה לייצג את האוכלוסיה כולה). אך לא פעם, עם פרסום תוצאות האמת, מסתבר שהם טעו. ברוב המקרים הסיבה לכך היא שסטטיסטיקה היא מנבא מוגבל ולא תמיד מדויק של המציאות.
הנה דוגמאות קטנות למסקנות מעולם הסטטיסטיקה (עברית):
https://youtu.be/o4oM-7UOYRQ
סרטון שמדגים כמה שסטטיסטיקה יכולה להטעות כשמבינים ממנה דברים לא נכונים (עברית):
http://youtu.be/cKHAfiqHwZc
הסבירות הגדולה שסטטיסטיקה תטעה (מתורגם):
https://youtu.be/sxYrzzy3cq8
והסטודנטים לסטטיסטיקה באוניברסיטה (עברית):
https://youtu.be/b-k13rnRFcU

יש בעולם מעל 6500 שפות שונות.
מביניהן, השפות הכי מדוברות בעולם הן סינית, אנגלית, ספרדית, ערבית ורוסית. כמות האנשים שמדברים שפות אלה היא הגדולה ביותר מכל שפה אחרת.
סין היא המדינה בעלת האוכלוסיה הגדולה בעולם ולכן הסינית היא השפה שמספרית הכי הרבה מדברים בה.
מנגד, הפכה השפה האנגלית במאה ה-20 לשפה הבינלאומית המנצחת ולכן רוב אזרחי העולם שמדברים שפה נוספת מדברים בה.
כך התפתחו שפות העולם (מתורגם):
http://youtu.be/iWDKsHm6gTA

למה סרטי המשך של להיטים קולנועיים לא יצליחו כמו הסרט הראשון?
איך זה שילדיהם של גאונים או כשרונות גדולים לא יהיו מוצלחים כמוהם?
למה ספורטאי לא ישבור ברצף שיאים?
האם ראיתם או קרה פעם משהו מדהים וחשבתם שהוא יקרה שוב, אבל הוא לא חזר על עצמו בפעם הבאה? - ובכן, זה נורמלי וזו תופעה ידועה בשם "תסוגה לממוצע" או רגרסיה לממוצע.
רגרסיה לממוצע היא תופעה מרתקת וטבעית, שמתגלית שוב ושוב בתחומים רבים, הן בטבע והן במעשים ידי אדם.
התופעה אומרת שהסבירות של התרחשויות קיצוניות ברצף, זו אחרי זו, היא נמוכה מאד. כלומר, אחרי התרחשות של אירוע קיצוני כלשהו, אם יש קשר חיובי בין ההתרחשויות (מה שנקרא במדע "מתאם סטטיסטי חיובי"), כמעט בוודאות לא יהיה האירוע הבא מסוגו כה קיצוני והוא יהיה קרוב יותר לממוצע.
מי שגילה את התופעה ופרסם אותה בסוף המאה ה-19 היה המדען האנגלי סר פרנסיס גולטון, מי שגילה את המתאם הסטטיסטי וגם אחראי לגילוי עקרון "חוכמת ההמונים". גולטון חקר את הרגרסיה לממוצע בזרעים ובגבהים של הורים וילדים והופתע לגלות כמה התופעה רווחת וכמה היא יכולה להיות שימושית לניבוי דברים כמו מגמות עתידיות בתחומים רבים, או שינויים במצבם של חולים.
הנה הסבר על התסוגה לממוצע:
https://youtu.be/GEmuEWjHr5c
והסבר מילולי של הרגרסיה לממוצע:
https://youtu.be/Qw8b_igoMTM

אי-ודאות היא אחד הדברים שמלווים אותנו בחיים. לא פעם אנו חשים בחוסר וודאות, מכיוון שאין לנו יכולת לחזות את מזג האוויר, תוצאות של אירועי ספורט, או תוצאות של בחירות. למצבים כאלו יש כלי שיכול לסייע - הִסְתַּבְּרוּת (Probability).
הסתברות היא מושג מתמטי שמבטא את הסבירות שמאורע מסוים יתרחש. לעיתים יש לנו מושג מה סביר שיקרה, גם אם איננו יודעים בודאות מה יקרה. תורת ההסתברות מכמתת את "הסביר" ומודדת אותו באופן מדויק.
מדידת הסתברות של מאורע מסוים היא בסקאלה שבין 0 ל־1. מאורע בלתי אפשרי מקבל הסתברות 0, בעוד הסתברות 1 ניתנת למאורע שיש ודאות מוחלטת שיקרה. לעיתים קורה שמשתמשים באחוזים, בין 0% ל־100%, כדי לבטא הסתברות.
כשאנו מטילים מטבע, ההסתברות שהוא יפול על צד מסוים שלו היא 0.5, כלומר שבממוצע המטבע תיפול על אותו צד באחת מכל שתי זריקות. באופן דומה, ההסתברות שהכדור ברולטה ייפול על כל אחד מהמספרים, היא שווה.
היסטורית יש להסתברות עבר ארוך. עוד במאה ה-16 עסקו בחישובי הסתברויות. מאז הלך הענף הזה במתמטיקה והתפתח, כשהשימוש בו מסייע בתחומי הכלכלה, העסקים, ההימורים ועוד.
כך למשל קובעות חברות ביטוח את מחיר ביטוח החיים על פי ההסתברות שהמבוטח ייפגע או ימות במהלך תקופת הביטוח. חזאי מזג אוויר בוחנים את ההסתברות לגשם, בכדי להציע תחזית אמינה.
גם מהמרים נעזרים בחישובים כדי לדעת את הסיכויים שיזכו בהגרלות או במשחקים וכך הלאה.
הנה הדרך שבה ניתן לראות הסתברות (מתורגם):
https://youtu.be/Kgudt4PXs28
הדגמת ההסתברות דרך ניחושים (מתורגם):
https://youtu.be/3V2omKRX9gc
בעיית מונטי הול מדגימה יפה את ההסתברות וכמה שאינה אינטואיטיבית (עברית):
https://youtu.be/4stFDiXWuYk
מה ההסתברות לזכות בפיס כלומר בלוטו (עברית)?
https://youtu.be/_vyjrgU7hng
ודוגמה להסתברות שנוגדת את האינטואיציה שלנו (מתורגם):
https://youtu.be/Ghbkv0MKV-w
סטטיסטיקה

משפט הקוף המקליד גורס שבסופה של הקלדת כל רצף ארוך מספיק של תווים אקראיים, יופיע כמעט בוודאות, כל טקסט אפשרי. התאוריה אומרת שאם תהיה ההקלדה אינסופית, יווצר בוודאות כל טקסט שהוא, כולל נבואות, טקסטים של שייקספיר ורשימות מכולת מאתמול. זהו סדר שנוצר מתוך כאוס.
מתמטיקאי צרפתי בשם אמיל בורל היה הראשון שכתב את הדברים. הוא ניסח זאת כך שניתן לומר שאם קוף יקליד תווים אקראיים במכונת כתיבה, לבסוף הוא יקליד גם את כל כתבי וויליאם שייקספיר.
בגישה זו ניתן לענות גם לטענה שנבואות קדומות ניבאו כל מיני אירועים שקרו במאה האחרונה (כולל עלית היטלר, רצח רבין ועוד). הם גורסים בפשטות שבתנ"ך ניתן למצוא "רמזים" לאירועים אלה ואחרים, אם רק מחפשים מספיק...
אבל מה ניתן להפיק מהקלדות אקראיות כמו מה שהקופים מקלידים? - משפט הקוף המקליד הוא ניסוי מחשבתי בלבד. בניסוי שערכו ב-2003 בגן חיות, הסתבר שקופי המקוק שקיבלו 6 מכונות כתיבה למשך חודש כתבו רק 5 עמודים, שרובם היו מלאים באות "S" והרסו את מכונות הכתיבה.
אתר שמדמה את הקופים המקלידים בעזרת תוכנה שיוצרת אינספור הקלדות אקראיות, הצליח להפיק 24 אותיות רצופות מתוך המחזה "הנרי הרביעי" של שייקספיר.
על תיאורמת הקוף האינסופי, או משפט הקוף המקליד (ללא מילים):
http://youtu.be/Imd_Vhg8Afk?t=13s
תיאור ציורי של תיאורת הקופים האינסופיים:
http://youtu.be/ipdRhgLWGXo
על תוצאותיו של הניסוי עם קופים ומכונות כתיבה:
http://youtu.be/pDUn7dDigvI
וסימולטור שמדמה את תיאורמת הקופים האינסופיים:
http://youtu.be/iSn8L6Uj5L8

ויזואליות עובדת הרבה יותר טוב מרשימות ארוכות של טקסט. זה ידוע כבר שנים רבות.
אינפוגרפיקה (Infographic) היא המחשת מידע (הדגמה) בעזרת אמצעים גרפיים מגוונים, כמו איורים, תמונות, אנימציה, גרפים, תרשימי זרימה ועוד.
שיטת האינפוגרפיקה משמשת להצגה פשוטה ומובנת יותר של תהליכים שונים, מידע מורכב וכבד, רצף אירועים וכדומה. המבוגרים, שאוהבים מילים קשות ומרשימות בלועזית, היו אומרים שהאינפוגרפיקה היא סוג של ויזואליזציה (המחשה ויזואלית) המלווה בהסברים טקסטואליים.
לתחום האינפוגרפיקה יש שורשים עתיקים, שמגיעים עד התרבות של סין העתיקה. בעידן המודרני נחשב פרופסור בשם אדוארד טאפטי לאבי האינפוגרפיקה היישומית המודרנית.
בשנים האחרונות הולכת האינפוגרפיקה ונעשית פופולארית. שילוב אינפוגראפיקה באינטרנט, ובמאמרים בעיתונות הפך נפוץ ושכיח מאד.
כולנו הרי יודעים שפעמים רבות היכולת של איור או צילום להמחיש רעיון מורכב או לסייע ביצירתיות וחשיבה יצירתית, היא טובה הרבה יותר מפסקאות ארוכות של מלל. כבר מזמן אמרו הרי הסבים והסבתות שלנו ש"תמונה טובה מאלף מילים".
הנה הסבר המושג אינפוגרפיקה:
https://youtu.be/M3fBmZR2fTU
באנימציה:
https://youtu.be/zbTYyl7WVd8
שימוש באינפוגרפיקה לסרטון הדרכה:
https://youtu.be/VCG_L5jEX0c
וכך מציגים מדינה באמצעות אינפוגרפיקה:
https://youtu.be/i9vzQJylSFg
או תפוח:
https://youtu.be/rzRZPAnJU1Q

גרף בועות (Bubble Chart) דומה לגרף פיזור בכך שהוא מציג נקודות במערכת צירים עבור שני משתנים, אך מוסיף את גודל הנקודה כמידע נוסף. למעשה, כל "בועה" בגרף היא נקודה שהשטח שלה (או הרדיוס שלה) משקפת משתנה שלישי.
כך ניתן לדוגמה לבנות גרף בועות שבו כל בועה היא מדינה בעולם: מיקום אופקי מייצג בו את התוצר לנפש במדינה, מיקום אנכי מייצג את תוחלת החיים וגודל הבועה מייצג את גודל האוכלוסייה. כך נראה בבת אחת את הקשר בין עושר לאריכות חיים וגם אילו מדינות הן גדולות באוכלוסייה - מדינות עם הרבה תושבים יהיו בועות גדולות ומדינות קטנות יהיו בועות קטנות.
כלומר, באמצעות גרף כזה אפשר להעביר בהצגה דו-ממדית שלושה ממדי מידע: מיקום אופקי (X), מיקום אנכי (Y) וגודל (Z) שניתן לראות באמצעות גודל הבועה.
ואגב, לפעמים משתמשים גם בצבע הבועות כדי לשקף משתנה רביעי, אבל לרוב שני צירים וגודל נותנים כבר תמונה עשירה.
#יתרונות
גרף בועות מאפשר להציג יותר מידע באותה תמונה. הוא מצטיין בהמחשת מערכות נתונים מורכבות שבהן שני משתנים לא מספרים את כל הסיפור. הבועות מוסיפות ממד חדש, אך מבלי לעבור לגרף תלת-ממדי שהוא שקשה יותר לקריאה.
היתרון הוא שניתן לזהות דפוסים שאולי היו נסתרים אם היו מציגים כל פעם רק שני משתנים. אפשר לראות שלושה משתנים קשורים. במקרה המדינות, למשל, ייתכן שנגלה שמדינות עם תוצר גבוה ותוחלת חיים גבוהה הן גם בעלות אוכלוסייה בינונית, ואילו מדינות עם אוכלוסייה עצומה הן לאו דווקא הכי עשירות.
#התאמה
גרף בועות מתאים במיוחד למצבים שבהם יש שלושה משתנים כמותיים לכל פריט ונרצה לבדוק את היחסים ביניהם. הרבה פעמים משתמשים בזה בכלכלה וחברה - למשל להצגת נתוני המדינות כפי שתואר (עושר, בריאות, גודל אוכלוסייה) או להשוואת ביצועי חברות עסקיות (ציר אחד יכול להיות רווח, ציר שני צמיחה וגודל הבועה הוא שווי השוק של החברה).
גם בשיווק אפשר להשתמש בגרף עם בועות. למשל, כשכל בועה היא מוצר. עם ציר X למחיר, ציר Y לשביעות רצון לקוחות וגודל הבועה עבור כמות המכירות. כך ניתן להבין היכן ממוקמים המוצרים בשוק ביחס לשביעות הרצון מהם מול מחירם.
#דוגמאות
בדוגמה אמיתית הוצג על-ידי הנס רוסלינג (Hans Rosling) גרף בועות מפורסם ובו הוא תיאר את התפתחות מדינות העולם. באותו גרף ראו על גבי הגרף בועה לכל מדינה. הציר האופקי היה ההכנסה, הציר האנכי תוחלת החיים, בעוד שגודל הבועה ייצג את גודל האוכלוסייה. כך ניתן היה לראות בקלות את הודו וסין עם אוכלוסיותיהם העצומות, כבועות גדולות ועולות בציר ההכנסה לאורך השנים.
דוגמה יומיומית יותר היא של חנות מקוונת שיכולה לנתח את מוצריה בעזרת גרף בועות. כל בועה מייצגת עבורה מוצר. המיקום האופקי בגרף מייצג את מחירו והמיקום האנכי את דירוג הלקוחות (בכוכבים למשל), בעוד גודל הבועה מייצג את כמות המכירות של אותו מוצר. מבט כזה יכול לגלות שאין קשר בין המחיר לדירוג, אבל כן רואים שמוצרים עם דירוג גבוה נמכרים יותר. זה ייראה בבירור כשבועות גדולות מרוכזות באזורי הדירוג הגבוה בגרף.
הנה הסבר של גרף הבועות:
https://youtu.be/iv0CT5H0yug
עשו ואל תעשו בגרף בועות:
https://youtu.be/Fygi3mQY0Ag
ודוגמאות לגרף בועות בתוכנת Excel:
https://youtu.be/Q1uiytD86OQ

בעולם יש כ-6500 שפות מדוברות. ביניהן יש גם כ-120 שפות סימנים לחרשים וסובלים מליקויי שמיעה.
חשוב לדעת, עם זאת, ש-2000 מתוך השפות שיש בעולם, מדוברות על ידי פחות מ-1000 איש. לרוב מדובר על שפות של שבטים קטנים המוגדרות כשפות בסכנת הכחדה.
השפה הסינית מנדרינית היא המדוברת ביותר בעולם. מעריכים שמעל מיליארד ו-200 מיליון איש מדברים בה, אם כי יש מקורות המציינים מספרים שונים.
הנה סרטון קצרצר על השפות הפופולריות בעולם:
https://youtu.be/GxrtddcYEwM
וכך נוצרו כל כך הרבה שפות בעולם לא גדול כמו שלנו (מתורגם):
https://youtu.be/iWDKsHm6gTA

מפת חום (Heatmap) מציגה טבלה של ערכים בשני ממדים כאשר הערכים מיוצגים כצבעים.
כלומר, יש לנו ציר אופקי וציר אנכי (למשל, ימים ושעות, או פריטים שונים מול תכונות שונות), ובנקודת המפגש של כל שני פרמטרים יש ערך מספרי שמיוצג על ידי צבע.
במפת חום לרוב משתמשים בסקאלה צבעונית. למשל, מכחול דרך צהוב עד אדום, כדי לציין מערך ערכים נמוכים עד גבוהים.
היתרון הוא שבמבט אחד ניתן לאתר דפוסים: אזורים חמים (בצבע בולט כמו אדום) לעומת קרים (כחול או צבע כהה) שמראים איפה הערכים גבוהים או נמוכים במיוחד.
לדוגמה, דמיינו heatmap שבו ניתן לראות את עומס המבקרים בחנות לאורך הימים והשעות. כל שורה מייצגת יום בשבוע וכל עמודה שעה ביום. בעוד הצבע הלבן-צהוב מצביע על שעות שיא עם הרבה לקוחות (צהרי היום ובערב), השחור-אדמדם מצביע על שעות שקטות (למשל באמצע הלילה או מוקדם בבוקר).
כך ניתן לראות במבט מהיר שבסופי שבוע (שבת-ראשון) בצהריים יש צבע בהיר מאוד, כלומר החנות עמוסה אז במיוחד.
#יתרונות
מפת חום מצטיינת ביכולת להראות הרבה מידע בתמונה אחת באופן אינטואיטיבי. היא טובה בזיהוי תבניות, כי העין שלנו מיד נמשכת לאזורים בולטים בצבעם. למשל, אם נשתמש במפת חום להצגת ציוני תלמידים במקצועות שונים (שורות תלמידים, עמודות מקצועות, וצבע = ציון), נוכל מיד להבחין באילו מקצועות כיתה שלמה חזקה (מה שייראה בצורת עמודה בולטת בצבע מסוים) או האם תלמיד ספציפי בולט לרעה או לטובה (שורה מסוימת עם צבעים קיצוניים).
#התאמה
מפת החום מתאימה במיוחד עבור נתונים בעלי שני ממדים של קטגוריות או רצף, כשעבור כל צירוף שלהם יש ערך מספרי.
זה יכול להיות זמנים מול מקומות (כמו בדוגמת החנות: לכל יום ושעה יש מספר של לקוחות), או אנשים מול תכונות (למשל, טבלת תלמידים וציוניהם בכמה מקצועות), או אפילו מטריצה של מתאם בין משתנים (כשרוצים לראות אילו משתנים קשורים, עם ערכים גבוהים בצבע בולט).
מפת חום שימושית גם למדעני נתונים בתחומים כמו ביולוגיה ובינה מלאכותית, כדי להציג מטריצות גדולות בצורה שקל לקלוט (כמו "DNA Microarray" בביולוגיה, שמציג ביטויי גנים שונים כדוגמאות צבע).
#דוגמאות
דוגמה מהחיים: רשת חברתית יכולה להציג למנהלי הקהילה מפה צבעונית של פעילות המשתמשים לפי שעה ויום: למשל, הצבעים יראו שבשעות הערב של סוף השבוע הפעילות באתר בשיאה (צבע חם מאוד) ואילו בשעות בוקר של אמצע השבוע הפעילות נמוכה (צבע קר).
דוגמה נוספת: אפליקציית תחבורה ציבורית עשויה להראות Heatmap של עומס נוסעים בתחנות שונות לאורך היום. כך ניתן לראות באילו תחנות ושעות יש עומס גדול (אדום), מה שעוזר בהקצאת משאבים כמו אוטובוסים נוספים בזמן הנכון.
מהי מפת חום?
https://youtu.be/Q3XFj3zJBuE
מפת חום בגוגל Sheet:
https://youtu.be/RuvbI3QcsFo
ליצור מפת חום בתוכנת אקסל:
https://youtu.be/4Ftu8ay4UKc
הרצאונת על מהי מפת חום ואיך להשתמש בה:
https://youtu.be/stgf2CfiXr4
ומפת חום מורכבת במיוחד:
https://youtu.be/NFbiSX6PYXo
מהי עקומת הפעמון?
נניח שנמדוד את הגבהים של אוכלוסיית ישראל ונביט על גרף שמציג את ההתפלגות שלהם (כמה אנשים יש מכל גובה). סביר שהגרף יהיה גבוה באמצע, כי הגבהים של רוב האוכלוסיה ממוצעים, הגרף יהיה נמוך במידות הגבוהות (יש יחסית מעט אנשים גבוהים בחברה) ונמוך בגבהים הנמוכים (יש גם מעט נמוכים בחברה הישראלית). הגרף שנקבל נראה כמו פעמון ולכן הוא נקרא "עקומת פעמון".
אם נשרטט גרף של התוצאות הסטטיסטיות של כמעט כל תופעה חברתית (ואולי לא כמעט), כנראה שנקבל גרף בצורת פעמון.
השמות הללו כמו עקומת הפעמון, עקומת ההתפלגות הנורמלית או עקומת גאוס הם שמות שונים לעקומה שמתארת את ההתפלגות הסטטיסטית של משתנים סביב הערך הממוצע שלהם.
זוהי התפלגות סטטיסטית שמשמשת בכל תחומי המדע, אך היא מקובלת מאד במדעי החברה. גאוס, המתמטיקאי שאחראי לגילויה כונה לא פעם "נסיך המתמטיקאים".
הנה עקומת הפעמון (עברית):
https://youtu.be/1X1WCmHJcQQ
וכך מוצג ה-IQ של האוכלוסייה בעקומת פעמון:
https://youtu.be/XQdenK0Pl38
נניח שנמדוד את הגבהים של אוכלוסיית ישראל ונביט על גרף שמציג את ההתפלגות שלהם (כמה אנשים יש מכל גובה). סביר שהגרף יהיה גבוה באמצע, כי הגבהים של רוב האוכלוסיה ממוצעים, הגרף יהיה נמוך במידות הגבוהות (יש יחסית מעט אנשים גבוהים בחברה) ונמוך בגבהים הנמוכים (יש גם מעט נמוכים בחברה הישראלית). הגרף שנקבל נראה כמו פעמון ולכן הוא נקרא "עקומת פעמון".
אם נשרטט גרף של התוצאות הסטטיסטיות של כמעט כל תופעה חברתית (ואולי לא כמעט), כנראה שנקבל גרף בצורת פעמון.
השמות הללו כמו עקומת הפעמון, עקומת ההתפלגות הנורמלית או עקומת גאוס הם שמות שונים לעקומה שמתארת את ההתפלגות הסטטיסטית של משתנים סביב הערך הממוצע שלהם.
זוהי התפלגות סטטיסטית שמשמשת בכל תחומי המדע, אך היא מקובלת מאד במדעי החברה. גאוס, המתמטיקאי שאחראי לגילויה כונה לא פעם "נסיך המתמטיקאים".
הנה עקומת הפעמון (עברית):
https://youtu.be/1X1WCmHJcQQ
וכך מוצג ה-IQ של האוכלוסייה בעקומת פעמון:
https://youtu.be/XQdenK0Pl38
איך היסטוגרמה מראה התפלגויות?
היסטוגרמה (Histogram) דומה במראה לגרף עמודות, אך היא משרתת מטרה שונה: היא מראה התפלגות של נתונים רציפים. ציר אחד (בדרך כלל אופקי) מחולק ל"טווחים" או "אשכולות" של ערכים (בין X ל-Y, Y ל-Z, וכו') והציר האחר מראה כמה נתונים נופלים בכל טווח כזה.
כל עמודה בהיסטוגרמה מייצגת את מספר המקרים או התצפיות שהתגלו בטווח ערכים מסוים. כך למעשה ההיסטוגרמה נותנת מושג על צורת ההתפלגות – האם רוב הנתונים מרוכזים בטווח צר, פזורים באופן אחיד, או אולי יש שני "שיאים" וכו'.
אם נאסוף, לדוגמה, את ציוני המבחן של 100 תלמידים, נוכל ליצור היסטוגרמה שבה כל עמודה מראה כמה תלמידים קיבלו ציון בטווח מסוים (נגיד 50-60, 60-70, 70-80, וכו'). כך אפשר לראות האם רוב הכיתה קיבלה ציונים גבוהים, נמוכים, או שהתפלגו באופן שווה.
#יתרונות
היסטוגרמה מצטיינת בהצגת התפלגות ערכים – משהו שגרף עמודות רגיל אינו עושה, כי גרף עמודות מציג כל קטגוריה בנפרד ולא טווח רציף.
בעזרת היסטוגרמה אפשר לזהות במהירות מאפיינים של הנתונים כמו שכיחות (כמה פעמים ערכים מופיעים בטווח מסוים), האם יש הטיה לכיוון גבוה או נמוך והאם הנתונים מרוכזים סביב ערך מרכזי או מפוזרים.
כך, למשל, אפשר לראות אם יש "זנב ארוך" – כלומר מעט ערכים רחוקים מהמרכז (מה שיראה כעמודה בודדת רחוקה מהשאר).
#התאמה
היסטוגרמה מתאימה במיוחד עבור נתונים מספריים רציפים בכמות גדולה, כאשר רוצים להבין את הצורה הכללית שלהם.
כל מצב שבו יש מדידה כמותית להרבה פרטים - ציוני תלמידים, גבהים של אנשים, משך זמן שלוקח לאנשים לבצע משימה, טמפרטורות יומיות בחודש – יתאים להיסטוגרמה.
מה שכן, חשוב שלנתונים יהיה טווח ערכים רחב מספיק כדי לחלק לטווחים (Bins) ולהפיק תובנות מצורת ההצטברות שלהם.
#דוגמאות
דוגמה מהחיים היא של מורה שיכול להכין היסטוגרמה של ציוני הבחינה בכיתה כדי לראות את פיזור הציונים. הציר האופקי הוא טווחי ציונים, בעוד הציר האנכי הוא מספר התלמידים בכל טווח. כך ניתן לבחון האם יש שתי פסגות (האם למשל קבוצה גדולה קיבלה ציונים נמוכים וקבוצה גדולה אחרת ציונים גבוהים) או שהציונים מרוכזים סביב ציון ביניים.
דוגמה נוספת: היסטוגרמה של גילאי תושבי עיר – ציר אופקי טווחי גיל (0-9, 10-19, 20-29 וכו') והציר האנכי מספר התושבים בכל טווח. כך העירייה יכולה לראות אם יש הרבה צעירים, הרבה מבוגרים וכו', דברים שיכולים להשפיע על תכנון וסוג השירותים לתושבים.
מהי היסטוגרמה, מתי להשתמש בה ואיך?
https://youtu.be/haJyaQObNwU
היסטוגרמה בעולם ההשקעות:
https://youtu.be/Xv8gh2exXeE
מה ההבדל בין היסטוריה לגרף עמודות?
https://youtu.be/JsEwJD1mYpU
היסטוגרמה? - מתי להשתמש באיזה גרף?
https://youtu.be/yrTB5JSQPqY
כך תבנו היסטוגרמה:
https://youtu.be/fHX7myclXyk
היסטוגרמה (Histogram) דומה במראה לגרף עמודות, אך היא משרתת מטרה שונה: היא מראה התפלגות של נתונים רציפים. ציר אחד (בדרך כלל אופקי) מחולק ל"טווחים" או "אשכולות" של ערכים (בין X ל-Y, Y ל-Z, וכו') והציר האחר מראה כמה נתונים נופלים בכל טווח כזה.
כל עמודה בהיסטוגרמה מייצגת את מספר המקרים או התצפיות שהתגלו בטווח ערכים מסוים. כך למעשה ההיסטוגרמה נותנת מושג על צורת ההתפלגות – האם רוב הנתונים מרוכזים בטווח צר, פזורים באופן אחיד, או אולי יש שני "שיאים" וכו'.
אם נאסוף, לדוגמה, את ציוני המבחן של 100 תלמידים, נוכל ליצור היסטוגרמה שבה כל עמודה מראה כמה תלמידים קיבלו ציון בטווח מסוים (נגיד 50-60, 60-70, 70-80, וכו'). כך אפשר לראות האם רוב הכיתה קיבלה ציונים גבוהים, נמוכים, או שהתפלגו באופן שווה.
#יתרונות
היסטוגרמה מצטיינת בהצגת התפלגות ערכים – משהו שגרף עמודות רגיל אינו עושה, כי גרף עמודות מציג כל קטגוריה בנפרד ולא טווח רציף.
בעזרת היסטוגרמה אפשר לזהות במהירות מאפיינים של הנתונים כמו שכיחות (כמה פעמים ערכים מופיעים בטווח מסוים), האם יש הטיה לכיוון גבוה או נמוך והאם הנתונים מרוכזים סביב ערך מרכזי או מפוזרים.
כך, למשל, אפשר לראות אם יש "זנב ארוך" – כלומר מעט ערכים רחוקים מהמרכז (מה שיראה כעמודה בודדת רחוקה מהשאר).
#התאמה
היסטוגרמה מתאימה במיוחד עבור נתונים מספריים רציפים בכמות גדולה, כאשר רוצים להבין את הצורה הכללית שלהם.
כל מצב שבו יש מדידה כמותית להרבה פרטים - ציוני תלמידים, גבהים של אנשים, משך זמן שלוקח לאנשים לבצע משימה, טמפרטורות יומיות בחודש – יתאים להיסטוגרמה.
מה שכן, חשוב שלנתונים יהיה טווח ערכים רחב מספיק כדי לחלק לטווחים (Bins) ולהפיק תובנות מצורת ההצטברות שלהם.
#דוגמאות
דוגמה מהחיים היא של מורה שיכול להכין היסטוגרמה של ציוני הבחינה בכיתה כדי לראות את פיזור הציונים. הציר האופקי הוא טווחי ציונים, בעוד הציר האנכי הוא מספר התלמידים בכל טווח. כך ניתן לבחון האם יש שתי פסגות (האם למשל קבוצה גדולה קיבלה ציונים נמוכים וקבוצה גדולה אחרת ציונים גבוהים) או שהציונים מרוכזים סביב ציון ביניים.
דוגמה נוספת: היסטוגרמה של גילאי תושבי עיר – ציר אופקי טווחי גיל (0-9, 10-19, 20-29 וכו') והציר האנכי מספר התושבים בכל טווח. כך העירייה יכולה לראות אם יש הרבה צעירים, הרבה מבוגרים וכו', דברים שיכולים להשפיע על תכנון וסוג השירותים לתושבים.
מהי היסטוגרמה, מתי להשתמש בה ואיך?
https://youtu.be/haJyaQObNwU
היסטוגרמה בעולם ההשקעות:
https://youtu.be/Xv8gh2exXeE
מה ההבדל בין היסטוריה לגרף עמודות?
https://youtu.be/JsEwJD1mYpU
היסטוגרמה? - מתי להשתמש באיזה גרף?
https://youtu.be/yrTB5JSQPqY
כך תבנו היסטוגרמה:
https://youtu.be/fHX7myclXyk
למה משמש גרף פיזור?
גרף פיזור (Scatter Plot) הוא סוג של גרף המציג נקודות בודדות במערכת צירים, כשכל נקודה מייצגת תצפית אחת עם שני ערכים: אחד לערך הציר האופקי (X) ואחד לערך הציר האנכי (Y). בדרך זו ניתן לראות קשר אפשרי בין שני משתנים – האם יש ביניהם מגמה משותפת, קוֹרֵלַצְיָה, קשר כלשהו - או שהם בלתי תלויים.
הנקודות מפוזרות במישור בהתאם לערכיהן. אם למשל הערכים נוטים לעלות יחד (כש-X גדול גם Y גדול), נראה שהנקודות מתגבשות בקו אלכסוני עולה. לעומת זאת, אם אין קשר, הן תהיינה מפוזרות בצורה עננית וללא כיוון ברור.
לדוגמה, נוכל לצייר גרף פיזור שבו כל נקודה היא תלמיד: המיקום האופקי הוא מספר שעות הלמידה שלו למבחן, והמיקום האנכי הוא הציון שקיבל. אם נראה שהנקודות יוצרות נטייה אלכסונית (ככל שלמדו יותר שעות הציונים שלהם עולים), נסיק מכך שיש קשר חיובי בין זמן הלימוד לציון.
לחילופין, אם המצב הוא שהנקודות פזורות ללא סדר, כשחלק שלמדו מעט קיבלו ציון גבוה ואחרים שלמדו הרבה קיבלו ציון נמוך, נבין מכך שאין קשר ברור.
#יתרונות
גרף פיזור מצטיין בהמחשת קשרים ותבניות בין שני משתנים כמותיים. בשונה מגרפים כמו עמודות או קו, כאן כל פרט מופיע בנפרד כנקודה, וכך רואים גם את הפיזור וגם את צברי נקודות, ריכוזים של נקודות.
יתרון נוסף של גרף הפיזור הוא באפשרות לזהות בקלות ערכים חריגים (outliers), כנקודות שרחוקות מכל השאר.
#התאמה
גרף פיזור מתאים במיוחד עבור בדיקת קוֹרֵלַצְיָה (בעברית מִתְאָם), קשר או תלות בין שני דברים שנמדדים באופן מספרי.
דוגמאות? - מה הקשר בין משקל לגובה של אנשים? או בין כמות שעות צפייה בטלוויזיה לציונים בבית הספר?
כלומר גרף פיזור יהיה הבחירה הטבעית לכל זוג של נתונים מספריים שחשוב לנו לדעת אם יש ביניהם קשר. לעיתים גם מוסיפים קו מגמה או מחשבים מִתאם, קורלציה (correlation) כדי לכמת את הקשר, אבל ויזואלית הגרף כבר נותן תחושה טובה של זה.
#דוגמאות
קבלו דוגמה מהחיים - חוקרת עשויה להשתמש בגרף פיזור כדי לבדוק את הקשר בין כמות הפעילות הגופנית השבועית של אנשים לבין לחץ הדם שלהם. כל אדם מיוצג בנקודה אית, כשציר ה-X הוא שעות הספורט בשבוע, בעוד ציר Y הוא רמת לחץ הדם. אם מתגלה שיותר ספורט נוטה להתאים ללחץ דם נמוך יותר (נקודות לכיוון אלכסון יורד), זה רמז לקשר שלילי בין המשתתנים (יותר פעילות, פחות לחץ דם).
דוגמה נוספת: גרף פיזור של גודל דירה (במ"ר) מול גובה שכר הדירה. אם אכן קיים קשר כזה בשוק הדיור, הרי שנקודות ערוכות בעלייה יראו שדירות גדולות יותר נוטות גם לעלות יותר.
הנה גרף פיזור:
https://youtu.be/1ZAxR2KgM0g
כך יוצרים גרף פיזור באקסל:
https://youtu.be/P4T41HT4Be8
כך קוראים אותו:
https://youtu.be/Qsges3fJVGM
גרף פיזור מצוין לקורלציות:
https://youtu.be/AxyDalIvKIA
וכך נבין את גרף הפיזור:
https://youtu.be/hKNFn2E2biw
גרף פיזור (Scatter Plot) הוא סוג של גרף המציג נקודות בודדות במערכת צירים, כשכל נקודה מייצגת תצפית אחת עם שני ערכים: אחד לערך הציר האופקי (X) ואחד לערך הציר האנכי (Y). בדרך זו ניתן לראות קשר אפשרי בין שני משתנים – האם יש ביניהם מגמה משותפת, קוֹרֵלַצְיָה, קשר כלשהו - או שהם בלתי תלויים.
הנקודות מפוזרות במישור בהתאם לערכיהן. אם למשל הערכים נוטים לעלות יחד (כש-X גדול גם Y גדול), נראה שהנקודות מתגבשות בקו אלכסוני עולה. לעומת זאת, אם אין קשר, הן תהיינה מפוזרות בצורה עננית וללא כיוון ברור.
לדוגמה, נוכל לצייר גרף פיזור שבו כל נקודה היא תלמיד: המיקום האופקי הוא מספר שעות הלמידה שלו למבחן, והמיקום האנכי הוא הציון שקיבל. אם נראה שהנקודות יוצרות נטייה אלכסונית (ככל שלמדו יותר שעות הציונים שלהם עולים), נסיק מכך שיש קשר חיובי בין זמן הלימוד לציון.
לחילופין, אם המצב הוא שהנקודות פזורות ללא סדר, כשחלק שלמדו מעט קיבלו ציון גבוה ואחרים שלמדו הרבה קיבלו ציון נמוך, נבין מכך שאין קשר ברור.
#יתרונות
גרף פיזור מצטיין בהמחשת קשרים ותבניות בין שני משתנים כמותיים. בשונה מגרפים כמו עמודות או קו, כאן כל פרט מופיע בנפרד כנקודה, וכך רואים גם את הפיזור וגם את צברי נקודות, ריכוזים של נקודות.
יתרון נוסף של גרף הפיזור הוא באפשרות לזהות בקלות ערכים חריגים (outliers), כנקודות שרחוקות מכל השאר.
#התאמה
גרף פיזור מתאים במיוחד עבור בדיקת קוֹרֵלַצְיָה (בעברית מִתְאָם), קשר או תלות בין שני דברים שנמדדים באופן מספרי.
דוגמאות? - מה הקשר בין משקל לגובה של אנשים? או בין כמות שעות צפייה בטלוויזיה לציונים בבית הספר?
כלומר גרף פיזור יהיה הבחירה הטבעית לכל זוג של נתונים מספריים שחשוב לנו לדעת אם יש ביניהם קשר. לעיתים גם מוסיפים קו מגמה או מחשבים מִתאם, קורלציה (correlation) כדי לכמת את הקשר, אבל ויזואלית הגרף כבר נותן תחושה טובה של זה.
#דוגמאות
קבלו דוגמה מהחיים - חוקרת עשויה להשתמש בגרף פיזור כדי לבדוק את הקשר בין כמות הפעילות הגופנית השבועית של אנשים לבין לחץ הדם שלהם. כל אדם מיוצג בנקודה אית, כשציר ה-X הוא שעות הספורט בשבוע, בעוד ציר Y הוא רמת לחץ הדם. אם מתגלה שיותר ספורט נוטה להתאים ללחץ דם נמוך יותר (נקודות לכיוון אלכסון יורד), זה רמז לקשר שלילי בין המשתתנים (יותר פעילות, פחות לחץ דם).
דוגמה נוספת: גרף פיזור של גודל דירה (במ"ר) מול גובה שכר הדירה. אם אכן קיים קשר כזה בשוק הדיור, הרי שנקודות ערוכות בעלייה יראו שדירות גדולות יותר נוטות גם לעלות יותר.
הנה גרף פיזור:
https://youtu.be/1ZAxR2KgM0g
כך יוצרים גרף פיזור באקסל:
https://youtu.be/P4T41HT4Be8
כך קוראים אותו:
https://youtu.be/Qsges3fJVGM
גרף פיזור מצוין לקורלציות:
https://youtu.be/AxyDalIvKIA
וכך נבין את גרף הפיזור:
https://youtu.be/hKNFn2E2biw
מהם סקרים ומה הבעיה בהם?
שמעון פרס אמר עליהם פעם ש"סקרים הם כמו בושם. אפשר להריח אותם אבל לא כדאי לשתות...". מי כמוהו חווה את כשלון הסוקרים, שמסתמכים על מדגמי ענק אך לא מצליחים לזהות את המגמות האמיתיות בבחירות.
סקר (Poll) הוא מדידה של משהו במדגם, חלק קטן באוכלוסיה, ושימוש באמצעים סטיטסטיים כדי להכליל על האוכלוסייה כולה. התחזיות של סקרים פוליטיים, למשל, מתבססות על מדגם קטן של קלפיות, שבו מתבקשים אנשים להצביע בקלפי המדגם, כמו שהצביעו בקלפי האמיתית. על המדגם להיות לא "מוטה", כלומר שיהיה בו ייצוג שווה של קבוצות שונות באוכלוסייה.
בשנים האחרונות הולכים הסקרים ומאבדים את היכולת לחזות מגמות פוליטיות. זו מגמה שהולכת ומתבררת בהרבה מאד מקומות. מישראל של בחירות 2015, בהן ניצח ראש הממשלה, בניגוד לכל הסקרים שחזו את נפילתו, דרך סקרים שהכזיבו בגדול בעולם כולו.
דוגמאות לכישלונות של סקרים לא חסרות. המפורסמים שביניהם הם תוצאות המהפך בבחירות בישראל ב-1977, ההפתעה המדהימה של הברקזיט במשאל העם האנגלי שהביא להיפרדות מגוש היורו והניצחון הבלתי צפוי של דונלד טראמפ בקמפיין הראשון שלו לנשיאות ארצות הברית.
אז מה הבעיה בסקרים?
מזה שנים מצביעים מומחים על הדרך שבה מתקבלות ומפוענחות לא נכון תוצאות המדגמים. הן מצביעות על נצחון של מי שלבסוף יתגלה כמובס במערכת הבחירות. שוב ושוב טופחות תוצאות האמת על פניהם של הסוקרים ומצליחה לערער את אמינותם.
מצד שני, לא פעם משפיעות תוצאות הסקרים על תוצאות הבחירות עצמן. זאת מכיוון שהבוחרים מחליטים למי להצביע בהתאם למה שהסקרים מראים. כך לדוגמה, אם הם קוראים בסקר שהליכוד עומד לנחול תבוסה בבחירות ובשל כך הם "חוזרים הביתה", להצביע לו ולהביא לניצחונו.
מצד אחד, הסקר הוא הכלי האובייקטיבי ביותר שעומד לרשות הפוליטיקאים. בעזרתו הם מנסים לנבא את התנהגות הבוחרים והעמדות שלהם.
מצד שני הניסיון כבר הוכיח עד כמה חשוב להתייחס אל הסקרים בזהירות. אם משתמשים בהם בלי להיות מודעים לחולשות ולבעיות שבהם - נוהגים בחוסר אחריות ובטפשות של ממש.
למשל, ההתעלמות מכך שבתנאים של קרבה לתיקו בהצבעה, המשמעות הפוליטית של הסטייה הסטטיסטית, סטייה שתמיד תהיה שם והיא נסבלת בכל סיטואציה אחרת, היא עצומה. במילים פשוטות, אם טראמפ והילרי מתחרים בצמידות, או שמתנגדי הברקזיט מתחלקים כמעט 50-50, הרי שהסקר לא יוכל לומר מי ינצח. כל סטייה קטנה תמליך צד אחר.
יש גם בעיות אחרות, כמו העובדה שתוצאות הסקר, גם אם נקבל אותן כמו שהן, נכונות רק ליום הסקר. בקמפיין פוליטי הופך כל יום לסיפור חדש והשינויים הללו הם כל כך משמעותיים, במיוחד במירוץ צמוד, שהסקר של שלשום שווה לניחוש פשוט.
בעיה נוספת היא אמינות הנסקרים. יותר ויותר אנשים נלחצים מלהודות בעובדות שונות שקשורות בתמיכה במועמד או בנושא שנוי במחלוקת. קשה להם להציב את עצמם בקבוצה הנרדפת על ידי דעת הקהל והתקשורת הדומיננטית והם מספרים לסוקר דבר אחד, בזמן שבקלפי הם עושים דבר הפוך.
בישראל למשל, יש טענה קבועה שיש מגזרים באוכלוסיה, שאינם משתפים פעולה. גם שינויים טכנולוגיים, במיוחד כניסת האינטרנט, הרשתות החברתיות, החדשות שכבר לא מתקבלות מכלי התקשורת הגדולים דווקא - כל אלו הפכו את הסקרים ויכולת הניבוי שלהם לבעייתיים מאד.
מצד שני, הסקרים, במיוחד הכמותיים שבהם, מהווים עדיין את כלי העבודה העיקרי של הפוליטיקאים ויועציהם. גורלות נחרצים על פיהם ובאין כלי אחר, מתקבלות על פי הסקרים (לרוב סקרי עומק) החלטות פוליטיות חשובות מאד, לפחות בתקופת מערכת בחירות, על פי תוצאות הסקרים הללו.
בתנאים כאלה, עיבוד הנתונים ופירושם על ידי הסוקרים ובאופן כללי המקצועיות שלהם, הופכים למרכיב הקובע ביכולת להתגבר על מגוון הבעיות שבשיטת הסקר.
מה הבעיה עם הסקרים של הבחירות? (עברית)
https://youtu.be/am0Bz86egv8
הסבר "לילדים" (עברית):
https://youtu.be/Us8pVTrmN6I
עולם הסקרים הפוליטיים (מתורגם):
https://youtu.be/ubR8rEgSZSU
ובארץ יש מי שמנסים לבדוק אותו (עברית):
https://youtu.be/c1odMcMrcpo
שמעון פרס אמר עליהם פעם ש"סקרים הם כמו בושם. אפשר להריח אותם אבל לא כדאי לשתות...". מי כמוהו חווה את כשלון הסוקרים, שמסתמכים על מדגמי ענק אך לא מצליחים לזהות את המגמות האמיתיות בבחירות.
סקר (Poll) הוא מדידה של משהו במדגם, חלק קטן באוכלוסיה, ושימוש באמצעים סטיטסטיים כדי להכליל על האוכלוסייה כולה. התחזיות של סקרים פוליטיים, למשל, מתבססות על מדגם קטן של קלפיות, שבו מתבקשים אנשים להצביע בקלפי המדגם, כמו שהצביעו בקלפי האמיתית. על המדגם להיות לא "מוטה", כלומר שיהיה בו ייצוג שווה של קבוצות שונות באוכלוסייה.
בשנים האחרונות הולכים הסקרים ומאבדים את היכולת לחזות מגמות פוליטיות. זו מגמה שהולכת ומתבררת בהרבה מאד מקומות. מישראל של בחירות 2015, בהן ניצח ראש הממשלה, בניגוד לכל הסקרים שחזו את נפילתו, דרך סקרים שהכזיבו בגדול בעולם כולו.
דוגמאות לכישלונות של סקרים לא חסרות. המפורסמים שביניהם הם תוצאות המהפך בבחירות בישראל ב-1977, ההפתעה המדהימה של הברקזיט במשאל העם האנגלי שהביא להיפרדות מגוש היורו והניצחון הבלתי צפוי של דונלד טראמפ בקמפיין הראשון שלו לנשיאות ארצות הברית.
אז מה הבעיה בסקרים?
מזה שנים מצביעים מומחים על הדרך שבה מתקבלות ומפוענחות לא נכון תוצאות המדגמים. הן מצביעות על נצחון של מי שלבסוף יתגלה כמובס במערכת הבחירות. שוב ושוב טופחות תוצאות האמת על פניהם של הסוקרים ומצליחה לערער את אמינותם.
מצד שני, לא פעם משפיעות תוצאות הסקרים על תוצאות הבחירות עצמן. זאת מכיוון שהבוחרים מחליטים למי להצביע בהתאם למה שהסקרים מראים. כך לדוגמה, אם הם קוראים בסקר שהליכוד עומד לנחול תבוסה בבחירות ובשל כך הם "חוזרים הביתה", להצביע לו ולהביא לניצחונו.
מצד אחד, הסקר הוא הכלי האובייקטיבי ביותר שעומד לרשות הפוליטיקאים. בעזרתו הם מנסים לנבא את התנהגות הבוחרים והעמדות שלהם.
מצד שני הניסיון כבר הוכיח עד כמה חשוב להתייחס אל הסקרים בזהירות. אם משתמשים בהם בלי להיות מודעים לחולשות ולבעיות שבהם - נוהגים בחוסר אחריות ובטפשות של ממש.
למשל, ההתעלמות מכך שבתנאים של קרבה לתיקו בהצבעה, המשמעות הפוליטית של הסטייה הסטטיסטית, סטייה שתמיד תהיה שם והיא נסבלת בכל סיטואציה אחרת, היא עצומה. במילים פשוטות, אם טראמפ והילרי מתחרים בצמידות, או שמתנגדי הברקזיט מתחלקים כמעט 50-50, הרי שהסקר לא יוכל לומר מי ינצח. כל סטייה קטנה תמליך צד אחר.
יש גם בעיות אחרות, כמו העובדה שתוצאות הסקר, גם אם נקבל אותן כמו שהן, נכונות רק ליום הסקר. בקמפיין פוליטי הופך כל יום לסיפור חדש והשינויים הללו הם כל כך משמעותיים, במיוחד במירוץ צמוד, שהסקר של שלשום שווה לניחוש פשוט.
בעיה נוספת היא אמינות הנסקרים. יותר ויותר אנשים נלחצים מלהודות בעובדות שונות שקשורות בתמיכה במועמד או בנושא שנוי במחלוקת. קשה להם להציב את עצמם בקבוצה הנרדפת על ידי דעת הקהל והתקשורת הדומיננטית והם מספרים לסוקר דבר אחד, בזמן שבקלפי הם עושים דבר הפוך.
בישראל למשל, יש טענה קבועה שיש מגזרים באוכלוסיה, שאינם משתפים פעולה. גם שינויים טכנולוגיים, במיוחד כניסת האינטרנט, הרשתות החברתיות, החדשות שכבר לא מתקבלות מכלי התקשורת הגדולים דווקא - כל אלו הפכו את הסקרים ויכולת הניבוי שלהם לבעייתיים מאד.
מצד שני, הסקרים, במיוחד הכמותיים שבהם, מהווים עדיין את כלי העבודה העיקרי של הפוליטיקאים ויועציהם. גורלות נחרצים על פיהם ובאין כלי אחר, מתקבלות על פי הסקרים (לרוב סקרי עומק) החלטות פוליטיות חשובות מאד, לפחות בתקופת מערכת בחירות, על פי תוצאות הסקרים הללו.
בתנאים כאלה, עיבוד הנתונים ופירושם על ידי הסוקרים ובאופן כללי המקצועיות שלהם, הופכים למרכיב הקובע ביכולת להתגבר על מגוון הבעיות שבשיטת הסקר.
מה הבעיה עם הסקרים של הבחירות? (עברית)
https://youtu.be/am0Bz86egv8
הסבר "לילדים" (עברית):
https://youtu.be/Us8pVTrmN6I
עולם הסקרים הפוליטיים (מתורגם):
https://youtu.be/ubR8rEgSZSU
ובארץ יש מי שמנסים לבדוק אותו (עברית):
https://youtu.be/c1odMcMrcpo
איך באנדורה חיים הכי הרבה שנים ומהי בכלל המדינה הזו?
תוחלת החיים בנסיכות הזעירה אנדורה היא הגבוהה בעולם. זה אומר שבנסיכות הקטנה והעשירה הזו אנשים חיים בממוצע מעל 83 שנה - תוחלת החיים הגדולה ביותר בעולם.
הנה סרטון על הטבע שבנסיכות אנדורה:
http://youtu.be/qanEizWxsGk
ומעט על מדינת אנדורה:
http://youtu.be/B10DiNXmFQM
תוחלת החיים בנסיכות הזעירה אנדורה היא הגבוהה בעולם. זה אומר שבנסיכות הקטנה והעשירה הזו אנשים חיים בממוצע מעל 83 שנה - תוחלת החיים הגדולה ביותר בעולם.
הנה סרטון על הטבע שבנסיכות אנדורה:
http://youtu.be/qanEizWxsGk
ומעט על מדינת אנדורה:
http://youtu.be/B10DiNXmFQM
מה עושים עם תרשים קופסה?
תרשים קופסה ("BoxPlot"), שנקרא גם תרשים תיבה, נותן סיכום חזותי של התפלגות נתונים בעזרת תיבה וקווים תוחמים מחוץ לתיבה, המכונים "שפמים".
תרשים הקופסה מספק 5 דברים על קבוצת הנתונים: המינימום, הרבעון התחתון, החציון, הרבעון העליון והמקסימום.
בתרשים מוצגים בצורה מרוכזת הערכים המרכזיים והפיזור של הנתונים:
#הרבעון התחתון והעליון - אלה גבולות התיבה שהם לרוב הרבעון התחתון והעליון. אלו ערכים שמתחת להם נמצאים 25% ו-75% מהנתונים.
חציון - הקו שבתוך התיבה. זהו החציון (Median), הערך האמצעי של הנתונים.
ערכי המינימום והמקסימום - ערכים שקל לזהות, כי הם מוצגים על ידי קצוות הקווים היוצאים מהקופסה ומכונים "שפמים" (whiskers). השפמים מיקומם בגבול הערכים הקיצוניים, שהם המינימום והמקסימום. ואגב, באנגלית קוראים לתרשימי קופסה גם "תרשימי קופסה ושפמים" (box and whisker plots).
נקודות בודדות מחוץ לטווח השפמים מסמנות ערכים חריגים. כלומר נתונים יוצאי דופן גבוהים או נמוכים במיוחד.
לדוגמה, בתרשים הקופסה יכולים להיות מוצגים ציוני מבחן של שתי כיתות: עבור כל כיתה יש "תיבה" אחת. ניתן לראות מצב בו בכיתה A החציון קצת גבוה מ-70, בעוד בכיתה B החציון הוא סביב 72. פיזור הציונים בכיתה B יכול להיות גדול יותר (התיבה ארוכה יותר וכך גם שפמי כיתה B הארוכים יותר - מה שמראה שהציונים בה מפוזרים על פני טווח רחב יותר). יכולה להיות גם נקודת עיגול מתחת לכיתה B, שמשמעותה היא למשל תלמיד שקיבל ציון חריג נמוך במיוחד לעומת שאר תלמידי כיתתו.
#יתרונות
תרשים קופסה מאפשר השוואה מהירה בין התפלגויות של קבוצות שונות. בגרף אחד אפשר לשים מספר "תיבות" זו ליד זו (כמו בדוגמת שתי הכיתות) ולהבין מיד באיזו קבוצה הערכים באופן כללי גבוהים יותר, איפה הפיזור רחב או צר יותר והאם יש חריגים.
זהו מידע שיהיה קשה לראות בגרפים פשוטים כמו גרף עמודות (שמציגים רק ממוצע או סכום ולא את פיזור הנתונים).
בנוסף, התרשים מספק הרבה מידע במבט מרוכז אחד: ממוצע או חציון, טווח בין-רבעוני (הקופסה), טווח כללי (השפמים) וחריגים, מבלי שנצטרך לראות כל נקודה ונקודה בנפרד.
#התאמה
תרשים הקופסה מתאים במיוחד עבור נתונים כמותיים, כאשר חשוב להבין את הפיזור והמגמה המרכזית שלהם, במיוחד בהשוואה בין כמה קבוצות.
למשל, בציוני מבחן של כמה כיתות שונות, בגבהים של זכרים מול נקבות או בהתפלגות הכנסות בערים שונות - בכל אלו מעניין לא רק מה הממוצע אלא איך הנתונים נפרשים סביבו.
תרשים קופסה שימושי גם בזיהוי ערכים חריגים שיכולים להיות חשובים. כמו, למשל, זיהוי ניסוי מדעי ש"תפס כיוון שונה" משאר התוצאות כי הוא חריג.
#דוגמאות
דוגמה מהחיים: דמיינו בית חולים שמשווה את זמן ההמתנה בחדר המיון בשלושה סניפים שונים. באמצעות תרשים קופסה, יוצג כל סניף בתיבה. אפשר לראות באיזה בית חולים זמן ההמתנה החציוני (חציון) קצר ביותר ובאיזה הפיזור גדול.
ייתכן שבבית חולים אחד לרוב ממתינים 10-20 דקות (תיבה קטנה), בעוד שבאחר הזמנים מגוונים ונפרשים מ-5 דקות ועד שעה (תיבה ושפמים גדולים יותר). מידע כזה עוזר לזהות איפה השירות עקבי ומהיר יותר.
עוד תרשים לדוגמה יכול להיות באמצעות Box Plot של ציוני שתי כיתות (כיתה A וכיתה B). הקו האדום בכל תיבה הוא החציון, הקופסה מראה את טווח הציונים האמצעי, והנקודות (כמו עיגול לבן) הן ערכים חריגים.
הנה הסבר של תרשים הקופסה:
https://youtu.be/Ck5HMTnvfw0
דוגמה שימושית לתרשים כזה:
https://youtu.be/b2C9I8HuCe4
חמשת הנקודות העיקריות בתרשים הקופסה:
https://youtu.be/E7ewAxluyt0
הנתונים שמראה תרשים קופסה:
https://youtu.be/EVm1NhGod1w
כך תקראו תרשים קופסה:
https://youtu.be/fHLhBnmwUM0
ותרשים קופסה בתוכנת אקסל:
https://youtu.be/f7rkB7c-zDw
תרשים קופסה ("BoxPlot"), שנקרא גם תרשים תיבה, נותן סיכום חזותי של התפלגות נתונים בעזרת תיבה וקווים תוחמים מחוץ לתיבה, המכונים "שפמים".
תרשים הקופסה מספק 5 דברים על קבוצת הנתונים: המינימום, הרבעון התחתון, החציון, הרבעון העליון והמקסימום.
בתרשים מוצגים בצורה מרוכזת הערכים המרכזיים והפיזור של הנתונים:
#הרבעון התחתון והעליון - אלה גבולות התיבה שהם לרוב הרבעון התחתון והעליון. אלו ערכים שמתחת להם נמצאים 25% ו-75% מהנתונים.
חציון - הקו שבתוך התיבה. זהו החציון (Median), הערך האמצעי של הנתונים.
ערכי המינימום והמקסימום - ערכים שקל לזהות, כי הם מוצגים על ידי קצוות הקווים היוצאים מהקופסה ומכונים "שפמים" (whiskers). השפמים מיקומם בגבול הערכים הקיצוניים, שהם המינימום והמקסימום. ואגב, באנגלית קוראים לתרשימי קופסה גם "תרשימי קופסה ושפמים" (box and whisker plots).
נקודות בודדות מחוץ לטווח השפמים מסמנות ערכים חריגים. כלומר נתונים יוצאי דופן גבוהים או נמוכים במיוחד.
לדוגמה, בתרשים הקופסה יכולים להיות מוצגים ציוני מבחן של שתי כיתות: עבור כל כיתה יש "תיבה" אחת. ניתן לראות מצב בו בכיתה A החציון קצת גבוה מ-70, בעוד בכיתה B החציון הוא סביב 72. פיזור הציונים בכיתה B יכול להיות גדול יותר (התיבה ארוכה יותר וכך גם שפמי כיתה B הארוכים יותר - מה שמראה שהציונים בה מפוזרים על פני טווח רחב יותר). יכולה להיות גם נקודת עיגול מתחת לכיתה B, שמשמעותה היא למשל תלמיד שקיבל ציון חריג נמוך במיוחד לעומת שאר תלמידי כיתתו.
#יתרונות
תרשים קופסה מאפשר השוואה מהירה בין התפלגויות של קבוצות שונות. בגרף אחד אפשר לשים מספר "תיבות" זו ליד זו (כמו בדוגמת שתי הכיתות) ולהבין מיד באיזו קבוצה הערכים באופן כללי גבוהים יותר, איפה הפיזור רחב או צר יותר והאם יש חריגים.
זהו מידע שיהיה קשה לראות בגרפים פשוטים כמו גרף עמודות (שמציגים רק ממוצע או סכום ולא את פיזור הנתונים).
בנוסף, התרשים מספק הרבה מידע במבט מרוכז אחד: ממוצע או חציון, טווח בין-רבעוני (הקופסה), טווח כללי (השפמים) וחריגים, מבלי שנצטרך לראות כל נקודה ונקודה בנפרד.
#התאמה
תרשים הקופסה מתאים במיוחד עבור נתונים כמותיים, כאשר חשוב להבין את הפיזור והמגמה המרכזית שלהם, במיוחד בהשוואה בין כמה קבוצות.
למשל, בציוני מבחן של כמה כיתות שונות, בגבהים של זכרים מול נקבות או בהתפלגות הכנסות בערים שונות - בכל אלו מעניין לא רק מה הממוצע אלא איך הנתונים נפרשים סביבו.
תרשים קופסה שימושי גם בזיהוי ערכים חריגים שיכולים להיות חשובים. כמו, למשל, זיהוי ניסוי מדעי ש"תפס כיוון שונה" משאר התוצאות כי הוא חריג.
#דוגמאות
דוגמה מהחיים: דמיינו בית חולים שמשווה את זמן ההמתנה בחדר המיון בשלושה סניפים שונים. באמצעות תרשים קופסה, יוצג כל סניף בתיבה. אפשר לראות באיזה בית חולים זמן ההמתנה החציוני (חציון) קצר ביותר ובאיזה הפיזור גדול.
ייתכן שבבית חולים אחד לרוב ממתינים 10-20 דקות (תיבה קטנה), בעוד שבאחר הזמנים מגוונים ונפרשים מ-5 דקות ועד שעה (תיבה ושפמים גדולים יותר). מידע כזה עוזר לזהות איפה השירות עקבי ומהיר יותר.
עוד תרשים לדוגמה יכול להיות באמצעות Box Plot של ציוני שתי כיתות (כיתה A וכיתה B). הקו האדום בכל תיבה הוא החציון, הקופסה מראה את טווח הציונים האמצעי, והנקודות (כמו עיגול לבן) הן ערכים חריגים.
הנה הסבר של תרשים הקופסה:
https://youtu.be/Ck5HMTnvfw0
דוגמה שימושית לתרשים כזה:
https://youtu.be/b2C9I8HuCe4
חמשת הנקודות העיקריות בתרשים הקופסה:
https://youtu.be/E7ewAxluyt0
הנתונים שמראה תרשים קופסה:
https://youtu.be/EVm1NhGod1w
כך תקראו תרשים קופסה:
https://youtu.be/fHLhBnmwUM0
ותרשים קופסה בתוכנת אקסל:
https://youtu.be/f7rkB7c-zDw
מהו גרף עמודות ולמה הוא טוב?
גרף עמודות (Bar Chart) הוא גרף השוואתי, עם ציר אחד בלבד, המציג השוואה בין קטגוריות שונות בעזרת מלבנים או עמודות שכל אחד מהם מייצג קטגוריה.
גובה כל עמודה (או אורך, אם העמודות אופקיות) מראה לנו כמה גדול הערך של אותה קטגוריה, למשל שכיחות של משהו, כמה ממנו יש. למשל, גרף של מספר תושבים בערים שונות יראה לנו עמודות שונות, שכל אחת מהן מציגה את גודל האוכלוסיה בעיר המסוימת, את שכיחות התושבים בה.
ערך גבוה מיוצג על-ידי עמודה גבוהה וערך נמוך על-ידי עמודה נמוכה. כלומר הגרף מסוג זה הוא פשוט לקריאה: ניתן מיד לראות בו בעמודות מי בין הקטגוריות היא "הכי גדולה" ומי "הכי קטנה", מי יותר ומי פחות.
לדוגמה, אפשר להשתמש בגרף עמודות כדי להציג את מספר התלמידים בכל כיתה בשכבה, כאשר לכל כיתה יש עמודה בגובה המתאים למספר התלמידים בה.
#יתרונות
גרף עמודות מצטיין בהשוואת גדלים בין פריטים או קבוצות שונות בצורה ישירה. בניגוד לגרף עוגה, שבו קשה להשוות בדיוק גדלים של פרוסות, כאן אפשר לראות בבירור ובמדויק איזו עמודה גבוהה יותר, גם אם ההפרשים לעתים זעירים.
גרף העמודות עדיף לעיתים גם על גרף קו, כשהנתונים אינם רציפים אלא מחולקים לקטגוריות נפרדות (למשל סוגי מוצרים, ערים, קבוצות גיל וכדומה).
#מתי?
גרף העמודות מתאים במיוחד עבור נתונים קטגוריים - כלומר נתונים המחולקים לקבוצות או לסוגים ברורים. גרף כזה מתאים להראות כמויות, סכומים או מספר פריטים בכל קטגוריה.
הגרף יעיל גם להצגת נתונים של תקופות (חודשים, שנים) כשרוצים להשוות תקופה לתקופה ולא בהכרח להראות מגמה רציפה.
#דוגמאות
למשל, השוואת כמות הגשמים בחודשי השנה באמצעות עמודות, כשלכל חודש עמודה המציגה את כמות המשקעים בו.
דוגמה נוספת: גרף עמודות יכול להראות כמה משתמשים יש לכל רשת חברתית (פייסבוק, אינסטגרם, טוויטר וכו'), כאשר כל רשת מיוצגת בעמודה. כך רואים איזו רשת היא בעלת מספר המשתמשים הגדול ביותר בצורה ברורה.
הנה גרף עמודות:
https://youtu.be/WTVdncVCvKo
גרף עמודות המציג מספר ערכים השוואתיים מטבלת שכיחות (עברית):
https://youtu.be/ZrBw7vTRsUs
דוגמה לגרף עמודות אופקי:
https://youtu.be/wlEQ6h9ilUU
ותבנית לילדים ליצירת דיאגרמת עמודות, גרף עמודות (עברית):
https://youtu.be/RjYKvcvlies
גרף עמודות (Bar Chart) הוא גרף השוואתי, עם ציר אחד בלבד, המציג השוואה בין קטגוריות שונות בעזרת מלבנים או עמודות שכל אחד מהם מייצג קטגוריה.
גובה כל עמודה (או אורך, אם העמודות אופקיות) מראה לנו כמה גדול הערך של אותה קטגוריה, למשל שכיחות של משהו, כמה ממנו יש. למשל, גרף של מספר תושבים בערים שונות יראה לנו עמודות שונות, שכל אחת מהן מציגה את גודל האוכלוסיה בעיר המסוימת, את שכיחות התושבים בה.
ערך גבוה מיוצג על-ידי עמודה גבוהה וערך נמוך על-ידי עמודה נמוכה. כלומר הגרף מסוג זה הוא פשוט לקריאה: ניתן מיד לראות בו בעמודות מי בין הקטגוריות היא "הכי גדולה" ומי "הכי קטנה", מי יותר ומי פחות.
לדוגמה, אפשר להשתמש בגרף עמודות כדי להציג את מספר התלמידים בכל כיתה בשכבה, כאשר לכל כיתה יש עמודה בגובה המתאים למספר התלמידים בה.
#יתרונות
גרף עמודות מצטיין בהשוואת גדלים בין פריטים או קבוצות שונות בצורה ישירה. בניגוד לגרף עוגה, שבו קשה להשוות בדיוק גדלים של פרוסות, כאן אפשר לראות בבירור ובמדויק איזו עמודה גבוהה יותר, גם אם ההפרשים לעתים זעירים.
גרף העמודות עדיף לעיתים גם על גרף קו, כשהנתונים אינם רציפים אלא מחולקים לקטגוריות נפרדות (למשל סוגי מוצרים, ערים, קבוצות גיל וכדומה).
#מתי?
גרף העמודות מתאים במיוחד עבור נתונים קטגוריים - כלומר נתונים המחולקים לקבוצות או לסוגים ברורים. גרף כזה מתאים להראות כמויות, סכומים או מספר פריטים בכל קטגוריה.
הגרף יעיל גם להצגת נתונים של תקופות (חודשים, שנים) כשרוצים להשוות תקופה לתקופה ולא בהכרח להראות מגמה רציפה.
#דוגמאות
למשל, השוואת כמות הגשמים בחודשי השנה באמצעות עמודות, כשלכל חודש עמודה המציגה את כמות המשקעים בו.
דוגמה נוספת: גרף עמודות יכול להראות כמה משתמשים יש לכל רשת חברתית (פייסבוק, אינסטגרם, טוויטר וכו'), כאשר כל רשת מיוצגת בעמודה. כך רואים איזו רשת היא בעלת מספר המשתמשים הגדול ביותר בצורה ברורה.
הנה גרף עמודות:
https://youtu.be/WTVdncVCvKo
גרף עמודות המציג מספר ערכים השוואתיים מטבלת שכיחות (עברית):
https://youtu.be/ZrBw7vTRsUs
דוגמה לגרף עמודות אופקי:
https://youtu.be/wlEQ6h9ilUU
ותבנית לילדים ליצירת דיאגרמת עמודות, גרף עמודות (עברית):
https://youtu.be/RjYKvcvlies
מהו ה"מס על טיפשות"?
הסיכויים הנמוכים לזכות בהימורים לא מפריעים לרבים להתחבר להימורים. אפילו מי שלומדים סטטיסטיקה ומבינים שהתוחלת לזכייה בהימורים היא נמוכה מהסכום שמושקע בהם, לא משתכנעים ומפסיקים. זו הסיבה שהימורים כמו הלוטו זכו כבר מזמן לכינוי "מס על טיפשות".
האם הכינוי המעליב הזה הוא מוצדק?
שניהם, גם מיסים וגם הימורים דוגמת הלוטו, מהווים מנגנונים יעילים ליצירת הכנסות ממשלתיות מהאזרח. אבל בעוד מסים הם לא עניין של החלטה אישית וכל אזרח מחויב לשלמם לשלטון, ההימורים הם וולנטריים - כל אחד מחליט אם הוא מעוניין או לא.
מצד שני, רק מי שלא מצליחים להשתכנע שמשחקי ההימורים הם עסקה כלכלית גרועה במיוחד הם משתתפי המשחק. מחקרים מצאו שוב ושוב שרובם הם מהשכבות הפחות מבוססות בחברה ומהעשירונים התחתונים. רבים מעידים שבימי התשלום של קצבאות הביטוח הלאומי, המהמרים מגיעים יותר, כדי להמר בתחנות מפעל הפיס.
אז זה אומר שהעניים הם טיפשים?
לא. זה אומר שגם אם אינם מבינים שהסיכויים לזכות קטנים מאד ושבסך הכל סיכוייהם להפסיד את כספם גדולים משמעותית מסיכויים להרוויח, יש שם משהו נוסף שמושך אותם לזה ויתכן שבדיוק את המשהו הזה מפסידים מי שלא מהמרים.
המשהו הזה שווה כסף ולפעמים לא מעט. מי שזוכרים את "קלפני המרפסת", אותם אנשים שהתכנסו בבית של אחד מהם למשחקי קלפים, "על כסף". זה היה נפוץ בעשורים הראשונים למדינה. רבים זוכרים שגם מי שהפסידו, מאד נהנה מהאירועים הללו.
הסיבה להנאה הזו היא חברתית והיא גם עובדת בהקשר של הימורי הלוטו, הטוטו ושאר הגרלות. הדיבור על העניין, החלפת הדעות, ההימורים, החדשות על "ההם שזכו" ו"ההוא שהתעשר" - כל אלו מספקים הרבה עניין, רכילות ודיונים חברתיים. זה גם שווה קצת, לא?
והמשהו הנוסף הזה, שאיש לא מדבר עליו, הוא שמי שיש לו פחות כסף - חולם לזכות בהגרלה. התקווה הזו ש"השבוע זה יקרה לי!" היא משהו שלרבים, במיוחד מקרב מי שהחיים לא מפנקים אותם ביום יום, היא יקרה מפז. ברור שרציונלית עדיף לא להמר ולהשקיע בדברים חשובים כמו חינוך הילדים, שיפור היכולות המקצועיות ואיכות החיים, אבל עדיין - לכל אחד יש את הבחירות שהוא עושה ויש מי שבוחרים בציפייה והתרגשות מהסיכוי.
אז אולי כשחושבים על זה להשתתף בהגרלות ולזרוק כסף עליהן זה נראה טיפשי, אבל לעתים ה"טיפשות" הזו ממלאת אותך בשמחה וחברה וגם "החכמים" משלמים לא מעט על הדברים האלה. זאת כל עוד ההימור הוא בסכום סביר, לא הופך להתמכרות להימורים, למכונות מזל או למרוצי סוסים ולא פוגע במשפחה ובתפקוד היומיומי של המהמר. אל תהמרו בבקשה ואם כן, אז רק במה שתוכלו להפסיד מבלי להיכנס לצרות.
הנה החלום - שיתקשרו אליך עם הפרס (עברית):
https://youtu.be/YzJwXm4goKo
הסיכויים הנמוכים לזכות בהגרלות כאלה לא מפריעה לאנשים להתמכר להימורים (עברית):
https://youtu.be/nRLbvXMFKtc
רבים מאלה שכן זוכים לא יודעים לנהל את הכסף שבו זכו ומתרוששים שוב:
https://youtu.be/0t3k5yh9Dh8
והסיפור המדהים על האיש שאיבד את הטופס הזוכה בהמון מיליונים של שקלים (עברית):
https://youtu.be/Q-luW5Nmqe8
הסיכויים הנמוכים לזכות בהימורים לא מפריעים לרבים להתחבר להימורים. אפילו מי שלומדים סטטיסטיקה ומבינים שהתוחלת לזכייה בהימורים היא נמוכה מהסכום שמושקע בהם, לא משתכנעים ומפסיקים. זו הסיבה שהימורים כמו הלוטו זכו כבר מזמן לכינוי "מס על טיפשות".
האם הכינוי המעליב הזה הוא מוצדק?
שניהם, גם מיסים וגם הימורים דוגמת הלוטו, מהווים מנגנונים יעילים ליצירת הכנסות ממשלתיות מהאזרח. אבל בעוד מסים הם לא עניין של החלטה אישית וכל אזרח מחויב לשלמם לשלטון, ההימורים הם וולנטריים - כל אחד מחליט אם הוא מעוניין או לא.
מצד שני, רק מי שלא מצליחים להשתכנע שמשחקי ההימורים הם עסקה כלכלית גרועה במיוחד הם משתתפי המשחק. מחקרים מצאו שוב ושוב שרובם הם מהשכבות הפחות מבוססות בחברה ומהעשירונים התחתונים. רבים מעידים שבימי התשלום של קצבאות הביטוח הלאומי, המהמרים מגיעים יותר, כדי להמר בתחנות מפעל הפיס.
אז זה אומר שהעניים הם טיפשים?
לא. זה אומר שגם אם אינם מבינים שהסיכויים לזכות קטנים מאד ושבסך הכל סיכוייהם להפסיד את כספם גדולים משמעותית מסיכויים להרוויח, יש שם משהו נוסף שמושך אותם לזה ויתכן שבדיוק את המשהו הזה מפסידים מי שלא מהמרים.
המשהו הזה שווה כסף ולפעמים לא מעט. מי שזוכרים את "קלפני המרפסת", אותם אנשים שהתכנסו בבית של אחד מהם למשחקי קלפים, "על כסף". זה היה נפוץ בעשורים הראשונים למדינה. רבים זוכרים שגם מי שהפסידו, מאד נהנה מהאירועים הללו.
הסיבה להנאה הזו היא חברתית והיא גם עובדת בהקשר של הימורי הלוטו, הטוטו ושאר הגרלות. הדיבור על העניין, החלפת הדעות, ההימורים, החדשות על "ההם שזכו" ו"ההוא שהתעשר" - כל אלו מספקים הרבה עניין, רכילות ודיונים חברתיים. זה גם שווה קצת, לא?
והמשהו הנוסף הזה, שאיש לא מדבר עליו, הוא שמי שיש לו פחות כסף - חולם לזכות בהגרלה. התקווה הזו ש"השבוע זה יקרה לי!" היא משהו שלרבים, במיוחד מקרב מי שהחיים לא מפנקים אותם ביום יום, היא יקרה מפז. ברור שרציונלית עדיף לא להמר ולהשקיע בדברים חשובים כמו חינוך הילדים, שיפור היכולות המקצועיות ואיכות החיים, אבל עדיין - לכל אחד יש את הבחירות שהוא עושה ויש מי שבוחרים בציפייה והתרגשות מהסיכוי.
אז אולי כשחושבים על זה להשתתף בהגרלות ולזרוק כסף עליהן זה נראה טיפשי, אבל לעתים ה"טיפשות" הזו ממלאת אותך בשמחה וחברה וגם "החכמים" משלמים לא מעט על הדברים האלה. זאת כל עוד ההימור הוא בסכום סביר, לא הופך להתמכרות להימורים, למכונות מזל או למרוצי סוסים ולא פוגע במשפחה ובתפקוד היומיומי של המהמר. אל תהמרו בבקשה ואם כן, אז רק במה שתוכלו להפסיד מבלי להיכנס לצרות.
הנה החלום - שיתקשרו אליך עם הפרס (עברית):
https://youtu.be/YzJwXm4goKo
הסיכויים הנמוכים לזכות בהגרלות כאלה לא מפריעה לאנשים להתמכר להימורים (עברית):
https://youtu.be/nRLbvXMFKtc
רבים מאלה שכן זוכים לא יודעים לנהל את הכסף שבו זכו ומתרוששים שוב:
https://youtu.be/0t3k5yh9Dh8
והסיפור המדהים על האיש שאיבד את הטופס הזוכה בהמון מיליונים של שקלים (עברית):
https://youtu.be/Q-luW5Nmqe8
מהי התפוצצות המידע וכמה מידע נוצר בעולם?
התפוצצות המידע (Information explosion) בעולם היא תופעה שלא תיאמן. אם פעם היו 33 מיליון הספרים השמורים בספריית הקונגרס האמריקני מרשימים אותנו בכמות שלהם, כדאי לדעת שהעולם האינטרנטי מייצר כיום כמות של כמה ספריות כאלה בכל יום!
רוצים נתונים? - בכל דקה מעלים משתמשים לפחות 100 שעות של וידאו לאתר האינטרנט יוטיוב. אל פייסבוק לבדה אנו מעלים כמות של 300 פטה-בייטים של מידע בכל שנה. הצילום הדיגיטלי מאפשר לנו להעלות בכל יום מעל שני מיליארד של תמונות חדשות. הן לבדן מציעות משהו כמו אקסה-בייט של מידע דיגיטלי ביום. בכל שנה אנו מייצרים מאות אקסה-בייטים, כמות מידע המקבילה לכמה מאות או אלפי ספריות קונגרס חדשות בשנה!
אין ספק שאחד הגורמים העיקריים שמאיצים את קצב יצירת המידע החדש הזה הוא תוכן הגולשים. אתרים אישיים, בלוגים, פורומים ורשתות חברתיות הביאו לכך שכל אחד מאיתנו יוצר המון מידע חדש בכל יום, לא פעם לאורך כל היום. לא כל המידע הזה חשוב. רובו מידע אישי וחסר חשיבות לאנושות, אבל בכל זאת - הוא נוצר ונערם בכמויות בלתי נתפסות ולא יימחק כל כך מהר. יש לו שימוש למישהו.
עוד סיבה חשובה להאצת ייצור המידע היא ענן המחשוב. הענן הוא פלטפורמה שמחיר האחסון בה הולך ויורד, מה שמאפשר ייצור של מידע בכמויות גדולות ואיחסונו בזיל זול. צניחת המחירים שדורשות ספקיות הענן הציבורי הגדולות, דוגמת אמזון, גוגל ומיקרוסופט, מגדילה את כמויות המידע הזה ללא הפסקה.
וגם אם לא נרצה בו, יש מי שאוגר את כל המידע הרב הזה למטרותיו. ההתייחסות לאוקיינוס המידע הזה היא כאל מאגר עצום שטומן בחובו הזדמנויות עסקיות והכנסות כספיות רבות.
הנה סרטון שמראה את כמויות המידע העצומות שמייצר המין האנושי כיום:
https://youtu.be/NTMkc0bLRlI
ומה הבעיה האנושית עם כמות המידע הזו:
https://youtu.be/VxfGuZ5Bsgk
ובחיוך, הנה האנשים שמוצפים במידע הרב ומתמכרים:
https://youtu.be/6MpfVD-c-QI
התפוצצות המידע (Information explosion) בעולם היא תופעה שלא תיאמן. אם פעם היו 33 מיליון הספרים השמורים בספריית הקונגרס האמריקני מרשימים אותנו בכמות שלהם, כדאי לדעת שהעולם האינטרנטי מייצר כיום כמות של כמה ספריות כאלה בכל יום!
רוצים נתונים? - בכל דקה מעלים משתמשים לפחות 100 שעות של וידאו לאתר האינטרנט יוטיוב. אל פייסבוק לבדה אנו מעלים כמות של 300 פטה-בייטים של מידע בכל שנה. הצילום הדיגיטלי מאפשר לנו להעלות בכל יום מעל שני מיליארד של תמונות חדשות. הן לבדן מציעות משהו כמו אקסה-בייט של מידע דיגיטלי ביום. בכל שנה אנו מייצרים מאות אקסה-בייטים, כמות מידע המקבילה לכמה מאות או אלפי ספריות קונגרס חדשות בשנה!
אין ספק שאחד הגורמים העיקריים שמאיצים את קצב יצירת המידע החדש הזה הוא תוכן הגולשים. אתרים אישיים, בלוגים, פורומים ורשתות חברתיות הביאו לכך שכל אחד מאיתנו יוצר המון מידע חדש בכל יום, לא פעם לאורך כל היום. לא כל המידע הזה חשוב. רובו מידע אישי וחסר חשיבות לאנושות, אבל בכל זאת - הוא נוצר ונערם בכמויות בלתי נתפסות ולא יימחק כל כך מהר. יש לו שימוש למישהו.
עוד סיבה חשובה להאצת ייצור המידע היא ענן המחשוב. הענן הוא פלטפורמה שמחיר האחסון בה הולך ויורד, מה שמאפשר ייצור של מידע בכמויות גדולות ואיחסונו בזיל זול. צניחת המחירים שדורשות ספקיות הענן הציבורי הגדולות, דוגמת אמזון, גוגל ומיקרוסופט, מגדילה את כמויות המידע הזה ללא הפסקה.
וגם אם לא נרצה בו, יש מי שאוגר את כל המידע הרב הזה למטרותיו. ההתייחסות לאוקיינוס המידע הזה היא כאל מאגר עצום שטומן בחובו הזדמנויות עסקיות והכנסות כספיות רבות.
הנה סרטון שמראה את כמויות המידע העצומות שמייצר המין האנושי כיום:
https://youtu.be/NTMkc0bLRlI
ומה הבעיה האנושית עם כמות המידע הזו:
https://youtu.be/VxfGuZ5Bsgk
ובחיוך, הנה האנשים שמוצפים במידע הרב ומתמכרים:
https://youtu.be/6MpfVD-c-QI
מהי אקראיות והאם מחשב מסוגל לייצר אותה?
אקראיות (Randomness) היא אי-סדר. כשאין שום תבנית או סדר מוגדרים, נוצרת אקראיות. מספר אקראי למשל, הוא מספר ש"הוגרל" ללא שום יכולת לחזות אותו, באופן מקרי לחלוטין.
הגרלת הכדורים של מפעל הפיס, או הגרלה של כרטיסים שעורבבו היטב בהגרלה - אלו נעשות תמיד בצורה אקראית, כדי שלכולם יהיה בדיוק אותו סיכוי לזכות. באופן דומה, ההסתברות לקבלת מספר כלשהו מקוביית משחק שנזרקת היא אחת מתוך 6 המספרים שעליה.
מחשב, לעומת אקראיות, הוא דטרמיניסטי. כל מספר שהמחשב יעלה על הדעת נקבע על ידי אירועים קודמים, או על ידי תכנות מראש. אין בו הגרלה או התנהגות בלתי צפויה. זה חלק מהיתרון שבו וסוד היציבות שלו, אבל בתחום האקראיות הוא לא משהו ואין בו שמץ של אקראיות.
ומכיוון שהמחשב אינו מסוגל לייצר אקראיות של ממש, כדי לקבל ממחשב מספר אקראי או סדרת מספרים שונה בכל הרצה של תכנית, על המחשב להשתמש במקור שתמיד יתן ערך שונה. המספרים שיופקו ממנו נראים אקראיים, אף שאינם כאלה.
כזה הוא למשל השעון הפנימי של המחשב, שמדמה מחולל אקראיות בצורה טובה מאד. אם ניקח למשל את מספר השניות שעבר מאז תאריך מסויים יתקבל ערך שהוא בלתי תלוי ולכן הוא קרוב לאקראיות של ממש. הפעלת מחולל, אלגוריתם שעוד יותר "מבלבל" אותו, יהפוך אותו למספר דומה ביותר למספר אקראי של ממש. בצורה דומה גם תנועות העכבר יכולות לספק מספרים שמדמים מספרים אקראיים.
הנה הדרך שבה מחשבים מתמודדים עם אקראיות (עברית):
http://youtu.be/Td3MUJ3I1Io
אקראיות (Randomness) היא אי-סדר. כשאין שום תבנית או סדר מוגדרים, נוצרת אקראיות. מספר אקראי למשל, הוא מספר ש"הוגרל" ללא שום יכולת לחזות אותו, באופן מקרי לחלוטין.
הגרלת הכדורים של מפעל הפיס, או הגרלה של כרטיסים שעורבבו היטב בהגרלה - אלו נעשות תמיד בצורה אקראית, כדי שלכולם יהיה בדיוק אותו סיכוי לזכות. באופן דומה, ההסתברות לקבלת מספר כלשהו מקוביית משחק שנזרקת היא אחת מתוך 6 המספרים שעליה.
מחשב, לעומת אקראיות, הוא דטרמיניסטי. כל מספר שהמחשב יעלה על הדעת נקבע על ידי אירועים קודמים, או על ידי תכנות מראש. אין בו הגרלה או התנהגות בלתי צפויה. זה חלק מהיתרון שבו וסוד היציבות שלו, אבל בתחום האקראיות הוא לא משהו ואין בו שמץ של אקראיות.
ומכיוון שהמחשב אינו מסוגל לייצר אקראיות של ממש, כדי לקבל ממחשב מספר אקראי או סדרת מספרים שונה בכל הרצה של תכנית, על המחשב להשתמש במקור שתמיד יתן ערך שונה. המספרים שיופקו ממנו נראים אקראיים, אף שאינם כאלה.
כזה הוא למשל השעון הפנימי של המחשב, שמדמה מחולל אקראיות בצורה טובה מאד. אם ניקח למשל את מספר השניות שעבר מאז תאריך מסויים יתקבל ערך שהוא בלתי תלוי ולכן הוא קרוב לאקראיות של ממש. הפעלת מחולל, אלגוריתם שעוד יותר "מבלבל" אותו, יהפוך אותו למספר דומה ביותר למספר אקראי של ממש. בצורה דומה גם תנועות העכבר יכולות לספק מספרים שמדמים מספרים אקראיים.
הנה הדרך שבה מחשבים מתמודדים עם אקראיות (עברית):
http://youtu.be/Td3MUJ3I1Io
מהו גרף עוגה ומה הוא מציג היטב?
גרף עוגה (Pie Chart), או דיאגרמת עוגה, הוא גרף נתונים ללא צירים המציג בפלחים צבעוניים את החלקים מתוך שלם.
יתרונו הוא בהצגת ההתפלגות של השלם לחלקים היחסיים, כמו גם של היחס שבין החלקים השונים ובין כל אחד מהם לבין השלם.
גרף עוגה נקרא כך כי צורתו כעין עוגה עגולה המחולקת לפרוסות. כל פרוסה מייצגת קטגוריה או חלק מסוים מתוך ה"עוגה" השלמה, וגודל הפרוסה (הזווית או השטח שלה) מראה את היחס או האחוז של אותו חלק מתוך השלם.
כל הפרוסות שמציגות חלוקת שלם לחלקים יוצרות מעגל שלם ולמעשה 100% מהנתון. גרף עוגה מאפשר לראות בבת-אחת איזה חלק תופסת כל קטגוריה מתוך הסך הכולל. כך ניתן להציג בעזרת גרף עוגה למשל את חלוקת התקציב חודשי של משק הבית: פרוסה אחת עבור אחוז ההוצאה על מזון, פרוסה אחרת עבור דיור, פרטסה לתחבורה, לבידור וכו'. כך רואים באילו סעיפים היה שיעור ההוצאות הגדול ביותר.
#יתרונות
גרף עוגה נותן תמונה מהירה של יחס החלקים בתוך שלם אחד. בניגוד לגרף עמודות המשווה כמויות מוחלטות, גרף העוגה מתמקד בהמחשת ההרכב היחסי – מה הגודל היחסי של כל חלק. הוא יעיל במיוחד כשיש רק כמה חלקים גדולים וברורים ומאפשר לזהות מיד למשל מה "הפרוסה הגדולה ביותר", או החלקים הגדולים יותר בחלוקה.
#מתי משתמשים בו?
גרף העוגה מתאים במיוחד להצגת אחוזים או חלקים מתוך סך הכל של השלם. בכל מצב שבו הנתונים הם חלקי סך (כלומר, סך הכול 100% מחולק בין קטגוריות), גרף עוגה יכול להתאים.
למשל, פילוח אוכלוסייה לפי קבוצות גיל, באחוזים מתוך כלל האוכלוסייה. או בפילוח חלוקת הזמן של סטודנט ביומיום שלו, כלומר כמה אחוזים מהזמן מוקדשים לכל פעילות.
#דוגמאות
יש דוגמאות מהמדע, כמו גרף עוגה שיכול להראות את ההרכב של האוויר שאנו נושמים: כ-78% חנקן, 21% חמצן, וכ-1% גזים אחרים. כל גז מיוצג בפרוסת עוגה בגודל מתאים.
דוגמה יומיומית היא חלוקת שעות היממה של תלמיד תיכון. אם ה"עוגה" כוללת 24 שעות, היא מחולקת לפרוסות – שינה, לימודים בבית הספר, שיעורי בית, שעות פנאי וכדומה. כך מראים בגרף אחד כמה משעות היום מוקדשות לכל פעילות.
הסבר של גרף העוגה:
https://youtu.be/GjJdZaQrItg
מצגת וידאו:
https://youtu.be/18o0iqU8Ke4
מהו גרף העוגה?
https://youtu.be/P2HIgjqIGiU
גרף עוגה (Pie Chart), או דיאגרמת עוגה, הוא גרף נתונים ללא צירים המציג בפלחים צבעוניים את החלקים מתוך שלם.
יתרונו הוא בהצגת ההתפלגות של השלם לחלקים היחסיים, כמו גם של היחס שבין החלקים השונים ובין כל אחד מהם לבין השלם.
גרף עוגה נקרא כך כי צורתו כעין עוגה עגולה המחולקת לפרוסות. כל פרוסה מייצגת קטגוריה או חלק מסוים מתוך ה"עוגה" השלמה, וגודל הפרוסה (הזווית או השטח שלה) מראה את היחס או האחוז של אותו חלק מתוך השלם.
כל הפרוסות שמציגות חלוקת שלם לחלקים יוצרות מעגל שלם ולמעשה 100% מהנתון. גרף עוגה מאפשר לראות בבת-אחת איזה חלק תופסת כל קטגוריה מתוך הסך הכולל. כך ניתן להציג בעזרת גרף עוגה למשל את חלוקת התקציב חודשי של משק הבית: פרוסה אחת עבור אחוז ההוצאה על מזון, פרוסה אחרת עבור דיור, פרטסה לתחבורה, לבידור וכו'. כך רואים באילו סעיפים היה שיעור ההוצאות הגדול ביותר.
#יתרונות
גרף עוגה נותן תמונה מהירה של יחס החלקים בתוך שלם אחד. בניגוד לגרף עמודות המשווה כמויות מוחלטות, גרף העוגה מתמקד בהמחשת ההרכב היחסי – מה הגודל היחסי של כל חלק. הוא יעיל במיוחד כשיש רק כמה חלקים גדולים וברורים ומאפשר לזהות מיד למשל מה "הפרוסה הגדולה ביותר", או החלקים הגדולים יותר בחלוקה.
#מתי משתמשים בו?
גרף העוגה מתאים במיוחד להצגת אחוזים או חלקים מתוך סך הכל של השלם. בכל מצב שבו הנתונים הם חלקי סך (כלומר, סך הכול 100% מחולק בין קטגוריות), גרף עוגה יכול להתאים.
למשל, פילוח אוכלוסייה לפי קבוצות גיל, באחוזים מתוך כלל האוכלוסייה. או בפילוח חלוקת הזמן של סטודנט ביומיום שלו, כלומר כמה אחוזים מהזמן מוקדשים לכל פעילות.
#דוגמאות
יש דוגמאות מהמדע, כמו גרף עוגה שיכול להראות את ההרכב של האוויר שאנו נושמים: כ-78% חנקן, 21% חמצן, וכ-1% גזים אחרים. כל גז מיוצג בפרוסת עוגה בגודל מתאים.
דוגמה יומיומית היא חלוקת שעות היממה של תלמיד תיכון. אם ה"עוגה" כוללת 24 שעות, היא מחולקת לפרוסות – שינה, לימודים בבית הספר, שיעורי בית, שעות פנאי וכדומה. כך מראים בגרף אחד כמה משעות היום מוקדשות לכל פעילות.
הסבר של גרף העוגה:
https://youtu.be/GjJdZaQrItg
מצגת וידאו:
https://youtu.be/18o0iqU8Ke4
מהו גרף העוגה?
https://youtu.be/P2HIgjqIGiU
מה זה גרף ולמה צריך גרפים?
גְּרָף (Graph Data), או גרף נתונים, הוא תיאור שבדרך כלל הוא דו-ממדי של מספר פרטי מידע המקושרים ביניהם על ידי יחסים כלשהם.
הגרף ישמש בדרך כלל להצגה חזותית של מידע כמותי. הוא מאפשר השוואה של הפריטים השונים זה לזה, בעזרת יחידות המידה שבדרך כלל מוצגות על הציר או על שני צירי הגרף. כי גם אם גרפים עתירי נתונים יוצגו לעתים עם מערכת צירים תלת-ממדית, בדרך כלל הם יוצגו בגרפים המבוססים על מערכת צירים דו-ממדית.
הציר האופקי, הציר שממש כמו האופק שאליו אנו מביטים נמתח לרוחב, יציג בדרך כלל את המשתנה. אם למשל נציג גרף של פופולריות של מוצר לאורך תקופה מסוימת, אז הציר האופקי יציג את הזמן, למשל את החודשים בשנה האחרונה.
הציר האנכי, העומד, יציג את הפונקציה. למשל בגרף של פופולריות המוצר בשנה האחרונה הציר הזה יציג את הפופולריות שלו, הפונקציה של המשתנה - כמה המוצר נמכר, או מה אחוז הנשאלים שאהבו את המוצר בסקר החודשי.
#למה צריך את זה?
גדולתו של הגרף היא בייצוג ויזואלי והשוואתי, באופן מופשט וללא מידע מיותר. כל זה לגבי קבוצת הפריטים או הנתונים, כשכולם מקושרים ביניהם באופן כלשהו.
יתרונם הגדול של הגרפים הוא בקלות ובמהירות של קליטת המידע מהם. גרף טוב יאפשר זיהוי מהיר של הקשר בין הנתונים והיחסים ביניהם, לעתים גם כולל המגמות שניתן לזהות בהם והחריגות שבין הנתונים.
#סוגי גרפים
ישנם כמה סוגי גרפים, כשלכל סוג יש יתרונות משלו ושימושים מתאימים לסוג המידע שהוא מציג היטב לצרכי ויזואליזציה של נתונים.
הגרפים הבולטים, השכיחים והשימושיים ביותר הם גרף עמודות, גרף קו, גרף עוגה, היסטוגרמה, גרף פיזור, תרשים קופסה (Box Plot), גרף בועות, גרף רציף, גרף נרות יפניים (גרף קו המציג את המדידות בניתוח טכני באופן משוכלל יותר מנקודות על הקו) ומפת חום (Heatmap) שהיא מעט שונה אבל נחשבת גם היא לסוג של גרף.
למחקר תאורטי נרחב זכו הגרפים במסגרת תורת הגרפים. ישנם סוגי גרפים שונים. להיכרות איתם ראו את תגית "סוגי גרפים".
הנה הסבר לילדים על מה זה גרף:
https://youtu.be/LW7I0Skjaew
כמה מסוגי הגרפים שמשתמשים בהם:
https://youtu.be/bmY28wdGL9M
איך יודעים באיזה גרף להשתמש בכל הקשר?
https://youtu.be/o7F-tbBl_hA
גרף נתונים בקו שמדגים את השינויים לאורך זמן (עברית):
https://youtu.be/siBhC7scAdQ
כך אפשר לזהות הטעיה באמצעות גרף (מתורגם):
https://youtu.be/E91bGT9BjYk
וגרף הנרות היפניים בעולם המסחר במניות (עברית):
https://youtu.be/FPZbtNtbMtc?long=yes
גְּרָף (Graph Data), או גרף נתונים, הוא תיאור שבדרך כלל הוא דו-ממדי של מספר פרטי מידע המקושרים ביניהם על ידי יחסים כלשהם.
הגרף ישמש בדרך כלל להצגה חזותית של מידע כמותי. הוא מאפשר השוואה של הפריטים השונים זה לזה, בעזרת יחידות המידה שבדרך כלל מוצגות על הציר או על שני צירי הגרף. כי גם אם גרפים עתירי נתונים יוצגו לעתים עם מערכת צירים תלת-ממדית, בדרך כלל הם יוצגו בגרפים המבוססים על מערכת צירים דו-ממדית.
הציר האופקי, הציר שממש כמו האופק שאליו אנו מביטים נמתח לרוחב, יציג בדרך כלל את המשתנה. אם למשל נציג גרף של פופולריות של מוצר לאורך תקופה מסוימת, אז הציר האופקי יציג את הזמן, למשל את החודשים בשנה האחרונה.
הציר האנכי, העומד, יציג את הפונקציה. למשל בגרף של פופולריות המוצר בשנה האחרונה הציר הזה יציג את הפופולריות שלו, הפונקציה של המשתנה - כמה המוצר נמכר, או מה אחוז הנשאלים שאהבו את המוצר בסקר החודשי.
#למה צריך את זה?
גדולתו של הגרף היא בייצוג ויזואלי והשוואתי, באופן מופשט וללא מידע מיותר. כל זה לגבי קבוצת הפריטים או הנתונים, כשכולם מקושרים ביניהם באופן כלשהו.
יתרונם הגדול של הגרפים הוא בקלות ובמהירות של קליטת המידע מהם. גרף טוב יאפשר זיהוי מהיר של הקשר בין הנתונים והיחסים ביניהם, לעתים גם כולל המגמות שניתן לזהות בהם והחריגות שבין הנתונים.
#סוגי גרפים
ישנם כמה סוגי גרפים, כשלכל סוג יש יתרונות משלו ושימושים מתאימים לסוג המידע שהוא מציג היטב לצרכי ויזואליזציה של נתונים.
הגרפים הבולטים, השכיחים והשימושיים ביותר הם גרף עמודות, גרף קו, גרף עוגה, היסטוגרמה, גרף פיזור, תרשים קופסה (Box Plot), גרף בועות, גרף רציף, גרף נרות יפניים (גרף קו המציג את המדידות בניתוח טכני באופן משוכלל יותר מנקודות על הקו) ומפת חום (Heatmap) שהיא מעט שונה אבל נחשבת גם היא לסוג של גרף.
למחקר תאורטי נרחב זכו הגרפים במסגרת תורת הגרפים. ישנם סוגי גרפים שונים. להיכרות איתם ראו את תגית "סוגי גרפים".
הנה הסבר לילדים על מה זה גרף:
https://youtu.be/LW7I0Skjaew
כמה מסוגי הגרפים שמשתמשים בהם:
https://youtu.be/bmY28wdGL9M
איך יודעים באיזה גרף להשתמש בכל הקשר?
https://youtu.be/o7F-tbBl_hA
גרף נתונים בקו שמדגים את השינויים לאורך זמן (עברית):
https://youtu.be/siBhC7scAdQ
כך אפשר לזהות הטעיה באמצעות גרף (מתורגם):
https://youtu.be/E91bGT9BjYk
וגרף הנרות היפניים בעולם המסחר במניות (עברית):
https://youtu.be/FPZbtNtbMtc?long=yes
