שלום,
נראה שכבר הכרתם את אאוריקה. בטח כבר גיליתם כאן דברים מדהימים, אולי כבר שאלתם שאלות וקיבלתם תשובות טובות.
נשמח לראות משהו מכם בספר האורחים שלנו: איזו מילה טובה, חוות דעת, עצה חכמה לשיפור או כל מה שיש לכם לספר לנו על אאוריקה, כפי שאתם חווים אותה.
»
«
 האם אפשר ללמוד מתמטיקה ברשת?
האם אפשר ללמוד מתמטיקה ברשת?
לימוד ברשת הוא היום אחד הטרנדים הכי מוצדקים שיש. בית הספר, כמו שאאוריקה מוכיחה יום יום, הוא לא המקום הבלעדי ואולי אף לא הטוב ביותר ללמוד היום. הרשת מכילה חומרי לימוד לכל רמה ולכל תחום אפשרי. רק צריך לבחור ולהחליט שלא מתייאשים.
אגב, זה העניין העיקרי, כי היום לומדים ברשת ובחינם אפילו קורסים אקדמיים של האוניברסיטאות היוקרתיות ביותר בעולם. הצרה היא שכמעט כולם נושרים בדרך ובממוצע מדהים ומבייש - רק 5% מאלו שהתחילו קורס כזה מסיימים אותו...
נחזור אלינו. אוסף הסרטונים של אלי נצר "שיעורטון" מציע לימוד מתמטיקה לתיכון בצורה קלה וידידותית. אלי, מורה למתמטיקה בתיכון בתל אביב, שילב את המילים שיעור וסרטון ויוצר בכל נושא סרטון קצר שמסביר ומלמד בקלות את הבעיה.
היתרונות של הלימוד עם הסרטונים הללו הוא שכל אחד יכול ללמוד את הנושא שהוא צריך, בזמן, בקצב ובמקום המתאים לו.
באתר "שיעורטון" יש מגוון ענק של שיעורטונים מתמטיים. הללו מסודרים וממויינים לפי תוכניות הלימוד ושאלוני הבגרות השונים.
הצפייה בסרטונים היא לגמרי בחינם. הלומדים יוכלו למצוא בכל דף שאלון גם פתרונות מלאים לשאלות הבגרות במתמטיקה, כשהם ממויינים לפי נושאים. כול הכבוד אלי!
הנה המורה שמלמד מתמטיקה באמצעות סרטוני לימוד מקוונים, אלי נצר (עברית):
https://youtu.be/En9Iv-I1Gbc
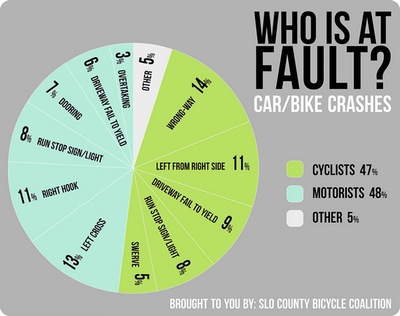 מהי סטטיסטיקה?
מהי סטטיסטיקה?
סטטיסטיקה היא תחום ידע שבו אוספים ומנתחים מידע כמותי, כדי להסיק מסקנות. כך למשל אוספים נתונים על אזרחי המדינה ומנתחים אותם וכך לומדים על חייהם, עיסוקיהם, מצבם הכלכלי ועוד. או שאוספים את נתוני הקליעה של שחקני כדורסל ואחרי ניתוח מגיעים למסקנות על הבולטים שבהם ואלו שעושים עבודה פחות טובה.
הסטטיסטיקה נחשבת מדע שאינו ניסויי, אך היא משרתת היטב את אנשי המדע. הסטטיסטיקאים משתמשים בכלים מתמטיים כדי לטפל בנתונים שלקוחים במרבית המקרים מהתחומים המדעיים של מדעי הטבע ומדעי החברה ומסייעים לגלות בהם דברים חשובים, שיכולים לתרום מאד.
אך לסטטיסטיקה יש גם מגבלות לא קטנות. למשל בכך שהיא עובדת טוב על מספרים גדולים ודי רע על מספרים קטנים. לדוגמה, הבה נביט על אדם שרגלו האחת בגיגית מים רותחים ורגלו השנייה בגיגית של מים קפואים. על פי הסטטיסטיקה יהיה מצבו טוב, שכן ממוצע החום שבין המים הרותחים והמים הקפואים יהיה נורמלי. עם זאת, ברור לנו שבמציאות אדם כזה יסבול מאד... אולי משום כך היה מי שהעיד שאמר פעם בנג'מין ד'יזראלי, ראש ממשלת בריטניה, "יש שלושה סוגי שקרים: שקרים, שקרים גסים וסטטיסטיקה"...
דוגמה נוספת לבעיה של הסטטיסטיקה היא היכולת לנבא ממדגם קטן על האוכלוסיה כולה. למשל, לא פעם חוזים הסוקרים הפוליטיים את תוצאות הבחירות. הם עושים זאת בעזרת מדגם (קבוצה קטנה שאמורה לייצג את האוכלוסיה כולה). אך לא פעם, עם פרסום תוצאות האמת, מסתבר שהם טעו. ברוב המקרים הסיבה לכך היא שסטטיסטיקה היא מנבא מוגבל ולא תמיד מדויק של המציאות.
הנה דוגמאות קטנות למסקנות מעולם הסטטיסטיקה (עברית):
https://youtu.be/o4oM-7UOYRQ
סרטון שמדגים כמה שסטטיסטיקה יכולה להטעות כשמבינים ממנה דברים לא נכונים (עברית):
http://youtu.be/cKHAfiqHwZc
הסבירות הגדולה שסטטיסטיקה תטעה (מתורגם):
https://youtu.be/sxYrzzy3cq8
והסטודנטים לסטטיסטיקה באוניברסיטה (עברית):
https://youtu.be/b-k13rnRFcU
 איך גרגרי אורז על לוח השחמט רוששו את המלך?
איך גרגרי אורז על לוח השחמט רוששו את המלך?
האם שאלתם את עצמכם פעם למה כדאי ללמוד מתמטיקה? - אם היה לכם ספק, אולי תסייע לכם האגדה שמסופרת בצורות שונות על ממציא משחק השחמט שהוזמן אל קיסר סין. הקיסר שאל מה ירצה כאות תודה על המשחק המופלא. לממציא השחמט הייתה בקשה מוזרה ודי צנועה: תן לי גרגרי אורז על משבצות לוח השחמט, כשבכל משבצת יש כמות כפולה של גרגרים מהקודמת לה - גרגיר אורז על המשבצת הראשונה, שני גרגירים על השנייה, ארבעה במשבצת השלישית וכן הלאה.
הקיסר, שהתרגל לבקשות גדולות יותר, שאל אם זה כל מה שירצה והממציא השיב לו בצניעות שדי לו בגרגירי האורז שביקש. "כמה טיפש יכול אדם להיות..." חשב ודאי הקיסר והסכים לבקשתו.
אבל מה גדול היה ההבדל שבין הקיסר הבור והממציא החכם. כל בעל ידע בסיסי במתימטיקה יזהה בחישוביו שהכמות של האורז שתונח על לוח השחמט היא בלתי נתפסת וגדלה באופן אקספוננציאלי, דוגמה מצוינת לגידול מעריכי בחשבון - מגרגר אחד ושני גרגרים במשבצות הראשונות תגדל הכמות לקילוגרם אורז במשבצת ה-15, טון אורז במשבצת ה-25, 1000 טון במשבצת ה-35 וכך הלאה.. במשבצת ה-55 יונח כל יבול האורז השנתי של העולם כולו ובמשבצת האחרונה תצטרך להיות כמות אורז שהיא גדולה מכל האורז שגדל אי-פעם בתולדות האדם!
אז אם יש לכם תכניות להמציא משהו גאוני והשליט שלכם הוא נדיב במיוחד, אולי כדאי לשקוד על לימודי המתמטיקה.
#דיון בכמות האורז
חישוב שקיבלנו ממשתמש אאוריקה מציע הסתייגות מתמטית מעניינת. הנה דבריו:
"קילוגרם אורז מכיל 45,000 גרגרים בממוצע. היבול השנתי של האורז בעולם הוא 700 מליון טון בממוצע של העשור האחרון. שהם 31.5E15 גרגרים.
הפרס הנדרש הוא 2^64, שזה סיכום של כל חזקות שתיים מאפס ועד 63. = 18.4E18
סך כל הפרס שווה ל-585 שנות גידול אורז. בהנחה שגידול האורז עלה עם השנים, ניתן להניח שכמות האורז שגדלה בששת אלפים שנות קיום העולם תספיק לממציא שלנו..."
אנו שואלים אתכם האם לדעתכם הכמות השנתית של ימינו היא זהה לכמות השנתית בעולם לפני אלף, אלפיים וששת אלפים שנה?"
הנה סרטון שמספר על אגדת האורז ולוח השחמט:
http://youtu.be/t3d0Y-JpRRg
וסרטון נוסף שמסביר את הסיפור במונחים החשבוניים של הגדילה המעריכית:
http://youtu.be/D9DvjkMMULw
 מה תרומת מכונת החישוב של בלז פסקל למחשב?
מה תרומת מכונת החישוב של בלז פסקל למחשב?
הפילוסוף, הפיזיקאי והמתמטיקאי הצרפתי בְּלֶז פסקל (Blaise Pascal) המציא למעשה את המחשב המכני הראשון בהיסטוריה. מכונת החישוב שבנה בשנת 1642 היא המחשב הראשון שידע לבצע פעולות חשבוניות כלשהן.
במשך כ-15 שנים מחייו בנה בלייז פסקאל מכונות חישוב שונות. היום מכנים אותן מכונות החישוב של פסקל (Pascal's calculators) והן הלכו והשתכללו. אולם "המחשב של פסקל", או "הפסקלין" כמו שקראו לו מאוחר יותר, נחשב באותה תקופה לגימיק או לאטרקציה בידורית.
למעט הממציא, איש לא התייחס למכונת החישוב שלו ברצינות מספקת. אולי זה משום שלא היה לה שימוש של ממש. ואגב, גם לשימוש מסחרי היא הייתה יקרה מדי.
מכונת החישוב של פסקאל, שנבנו ממנה כ-50 יחידות בלבד, ביצעה פעולות חשבוניות פשוטות כמו חיבור וחיסור. היא אפילו ידעה להעביר ספרות מושאלות - ספרות שיעברו לעשיריה הבאה, ממש כמו בתרגילים כתובים, מעמודה לעמודה.
במהלך השנים הבאות תשוכלל הפסקלין על ידי המתמטיקאי הגרמני גוטפריד לייבניץ, שיוסיף לה את האפשרות לפעולת הכפל.
כך פעלה מכונת החישוב של בלייז פסקאל:
http://youtu.be/3h71HAJWnVU
וקיצור חייו של בלז פסקאל:
https://youtu.be/IDMdnJDN1f4
 מהו פאי?
מהו פאי?
הפאי הוא מספר אי רציונאלי, מציין את היחס בין היקף מעגל לקוטרו. זהו מספר מסתורי, שמתמטיקאים וחובבי מתמטיקה מוקסמים ממנו כבר דורות רבים. ערכו של פאי שווה בקירוב ל 3.14.
הפאי מסומן באות היוונית π. הבבלים, ממציאי הגלגל, גילו אותו כבר לפני ששת אלפים שנה. התגלית של התופעה המרתקת של פאי, הייתה שבכל גודל מעגל שהוא, תוצאת החילוק של היקף המעגל ברדיוס שלו תהיה תמיד אותו המספר. 4000 שנה אחריהם, הצליחו מדעני מצרים העתיקה להגיע לערך מקורב של פאי. ארכימדס היווני הציג לראשונה, כבר במאה ה-3 לפני הספירה, שיטה שמאפשרת לאמוד את π.
הראשון שהצליח לחשב את פיי בדיוק גבוה היה אויילר. פיתוח החשבון הדיפרנציאלי והאינטגרלי סייע לו מאד והוא חישב את פאי עד 153 ספרות אחרי הנקודה. כמו הרבה דברים שאויילר תרם למתמטיקה, הוא גם זה שהעניק לפיי את שמו.
כיום, בעידן המחשב, המתמטיקאים עובדים על אלגוריתמים ונוסחאות אלגנטיות לחישוב פאי. השיא שנקבע עד 2011 הוא של 10 טריליון ספרות אחרי הנקודה!
הנה סרטון על משמעותו של הפיי (מתורגם):
http://youtu.be/9a5vHXsUvUw?t=13s
שיר לימודי באנגלית, להיכרות עם חישוב פאי:
http://youtu.be/eiHWHT_8WrE
מלחין שהחליט להלחין את המספר וכך לזכור אותו:
https://youtu.be/wM-x3pUcdeo
והביטוי המוסיקלי של המספר פאי ויחס הזהב שבנוי עליו:
https://youtu.be/9mozmHgg9Sk?long=yes
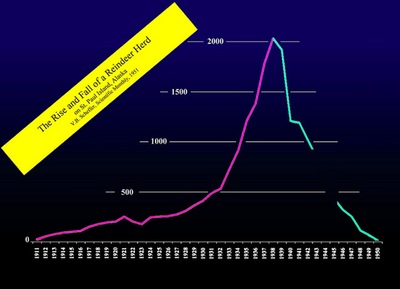 מהי גדילה מעריכית או אקספוננציאלית?
מהי גדילה מעריכית או אקספוננציאלית?
אם ניקח שטרות כסף עשויי נייר ונניח אותם זה על זה, כשכל פעם אנו מכפילים את מספר השטרות שלפנינו פי שניים, נקבל כבר אחרי 42 הכפלות הר של שטרות, כה גבוה עד שיגיע מפני הקרקע של כדור הארץ ועד לירח - מרחק מדהים של 380 אלף קילומטרים!
המספר המדהים הזה נובע מהגידול המעריכי (Exponential growth) של מספר השטרות.
גידול מעריכי, גדילה אקספוננציאלית, גדילה מעריכית, צמיחה מעריכית, גידול גאומטרי, טור גאומטרי ועוד הרבה שמות דומים - כולם מייצגים קצב גידול תלול במיוחד, שגדל בהכפלות ומשום כך הוא מהיר במיוחד.
לגידול האקספוננציאלי יש דוגמאות רבות בטבע. מסתבר שאם לא יאיימו עליהם מחלות או טורפים, תגדל אוכלוסיית החיידקים גדילה מעריכית, שתחדול לגדול רק כשייגמרו חומרי המזון על פני כדור הארץ, או שתורעל מחומרי הפסולת שהיא תשאיר אחריה.
באופן דומה יגדלו בגידול אקספוננציאלי גם אוכלוסיות של וירוסים שאין מולם חיסון (כמו שגילינו בהתפשטות המהירה של וירוס הקורונה), בשמרים שהם פטריות ומתפתחים במהירות ובחרקים שבבית הגידול שלהם יש מזון ואין איום עליהם.
גם בני אדם משתמשים בצמיחה מעריכית שכזו, במיזמים אנושיים שונים. "חוק מור" למשל, קבע שמהירות המחשבים מוכפלת כל שנה וחצי, מה שהופך את מהירותם לצומחת צמיחה אקספוננציאלית. כך גם מתנהגת ריבית דריבית, שנותנת החזר מעריכי למלווים, בתנאי כמובן שהתנאים נשארים קבועים, כולל שער הריבית.
משווקים בשיווק רב-שכבתי, כמו גם נוכלים ב"תרמיות פונזי" וב"משחקי פירמידה" - גם הם בונים את העיסקה על כך שכל מצטרף מגייס מספר אנשים, שיגייסו כל אחד כמה אחרים וכך הלאה. כך צומחת ההכנסה של כל משתתף, לא רק מרווחיו שלו, אלא גם מהמתגייסים שיצטרפו במורד השרשרת שמתחתיו - מגוייסיו, מגוייסיהם וכל מי שיגויס בהמשך.
בפיסיקה התגלה שבתגובת שרשרת גרעינית, שהיא הבסיס לכלי נשק גרעיני, פוגע כל גרעין אורניום שעבר ביקוע גרעיני, בגרעינים אחרים וגורם לביקועם, מה שיגרום לכל אחד מהם לפגוע בגרעינים אחרים ולבקעם וחוזר חלילה. אז אתם כבר יודעים איזו גדילה זו שיוצרת את הפיצוץ הנורא הזה - גדילה מעריכית, או בלעז: גידול אקספוננציאלי.
הנה סרטון שמדגים את הגדילה המעריכית (מתורגם):
https://youtu.be/AmFMJC45f1Q
התחזית של מלתוס מסוף המאה ה-19 על התפוצצות עתידית של אוכלוסיית העולם:
http://youtu.be/vZVOU5bfHrM
הכלכלה - האם היא תצמח לנצח?
https://youtu.be/mT3P0YSNonE
הסבר מתמטי (עברית):
https://youtu.be/6HsnjP0NzfE
יש מי שמסביר בעזרת הצמיחה המעריכית מדוע כדאי לבנות מסגרות פוליטיות "ללא כוכבים" (עברית):
https://youtu.be/Exg6ZdUpvkw
ושיעור באקדמיית קאן על גדילה מעריכית (עברית):
https://youtu.be/VZTDP9MvqLw?long=yes
 מיהו המתמטיקאי בלז פסקל שגם המציא את מכונת החישוב?
מיהו המתמטיקאי בלז פסקל שגם המציא את מכונת החישוב?
כנער במאה ה-17, שרצה לבלות זמן רב יותר עם אביו העסוק בחישובי מיסים עבור מלך צרפת, הוא המציא מכונת חישוב מכנית שתקל על אביו את החישובים החשבוניים ותפנה לו זמן לשחק איתו - עם בנו, בלז פסקל (Blaise Pascal).
ואכן, גם כשגדל היה הצרפתי בְּלֶז פסקל איש מדע רב-תחומי פעיל ומבריק. הוא פעל כמתמטיקאי, פיזיקאי ופילוסוף. מי שכבר מילדותו התעניין במספרים ובחשבון, הצליח ללמד את עצמו את חוקי הגאומטריה ומצא פתרונות מקוריים לבעיות גאומטריות שחלקן העסיקו מתמטיקאים מבוגרים. כמי שהחל מוקדם, הוא גם מת מוקדם. בגיל 39 הוא סיים את חייו, ובכל זאת הספיק לא מעט.
פסקל השתמש בכל כשרונו המתמטי כדי לבנות את מכונת החישוב המכאנית, אולי הראשונה בהיסטוריה - מכונת ה"פסקלין". המכונה שפיתח כדי לסייע בחישובי המס של אביו, נציב מס מטעם המלך, הייתה גאונית לזמנה וידעה לבצע פעולות חיבור וחיסור באמצעות גלגלי שיניים.
במאה ה-20 ידעו ראשוני המחשב להוקיר אותו כשקראו על שמו את שפת התכנות "פסקל".
אבל פסקל המגוון לא עסק רק במכונות חישוב שהקדימו את זמנן. הוא גם ניסח את הבסיס לתורת ההסתברות, ביחד עם המתמטיקאי פרמה. תורת ההסתברות שיצרו השניים היא מיסודות המדע המודרני.
הנה קצת על פסקל:
https://youtu.be/vu0nVuntD7g
סיפורו של פסקל:
https://youtu.be/xTaAx-f8mW8
סרטון על חייו:
https://youtu.be/IDMdnJDN1f4
הסבר המשולש של פסקל (ללא מילים):
http://youtu.be/YUqHdxxdbyM
והביוגרפיה המורחבת מעט של פסקל:
https://youtu.be/Tu1xNSEemuc
 איך ליצור רצועת מביוס לבד?
איך ליצור רצועת מביוס לבד?
 כמה מנגינות אפשר להמציא בכלל?
כמה מנגינות אפשר להמציא בכלל?
מספר המנגינות האפשריות הוא עצום, אבל ראשית כדאי שנקבע מה האורך שאנו רוצים לבדוק. אם מנגינה היא בת 8 צלילים, הרי שניתן לחבר כמעט 80 מיליארד מנגינות כאלה, מבלי לחזור על עצמן. אם תרצו לדעת את המספר המדויק של המנגינות האפשריות באורך כזה, במרווחים של 12 חצאי טונים בסולם, מדובר ב-78,364,164,096 אפשרויות בדיוק.
אז האם אין כמעט סיכוי שמנגינות יהיו כל כך דומות לאחרות? - אז זהו, שלא פעם זה קורה ואנחנו שמים לב ששירים מזכירים שירים אחרים שאנו מכירים.
התשובה היא תבניות. על אף שלכאורה יש לנו ביליוני אפשרויות של מנגינות שניתן לחבר, אנחנו נוטים לחבר מנגינות דומות ומוסיקה דומה לזו שכבר יש ושממנה אנו נהנים. אנחנו נוטים להשתמש בתבניות מוכרות לנו, כי אלה תבניות שאנו מתחברים אליהן תרבותית, מוסיקלית, מראש. הרי אם נכתוב שיר רוק, הרי שככל הנראה אנו חובבי רוק ומכירים שירי רוק, כך שמראש השיר יהיה בסגנון ועם מאגר ההשפעות "הרוקיות" ששמענו בעבר. לפעמים עלולות להיות בדמיון הזה אפילו היבטים משפטיים, של הפרת זכויות יוצרים.
כמובן שיש אנשים שנוטים יותר אל המוכר, גם אם לא במודע, ויש מקוריים יותר, פורצי דרך, אנשים שגם כשהם פועלים בסגנון מסוגלים להמציא לחנים מעניינים ומקוריים יותר. אבל זה כבר הבדל בין אנשים, יכולתם הקוגניטיבית והיצירתית ולא מתמטיקה. כי כמו "חוק העדר" שמושך את מרבית האנשים, מבלי שהם שמים לב לכך, להיצמד לאנשים, למשל על חוף ים ענקי וריק, ולא ללכת לשבת רחוק מכולם, כך גם כאן - מרבית המלחינים לא באמת יתרחקו מ"המוכר והטוב", מבחינתם.
הנה סרטון ארוך שמסביר את העניין בצורה מעניינת ורחבה אף יותר:
https://youtu.be/DAcjV60RnRw?long=yes
שימו לב לתבנית הרמונית בת 4 אקורדים, שמשמשת שוב ושוב לכתיבה של אינספור להיטי ענק:
https://youtu.be/oOlDewpCfZQ

לימוד ברשת הוא היום אחד הטרנדים הכי מוצדקים שיש. בית הספר, כמו שאאוריקה מוכיחה יום יום, הוא לא המקום הבלעדי ואולי אף לא הטוב ביותר ללמוד היום. הרשת מכילה חומרי לימוד לכל רמה ולכל תחום אפשרי. רק צריך לבחור ולהחליט שלא מתייאשים.
אגב, זה העניין העיקרי, כי היום לומדים ברשת ובחינם אפילו קורסים אקדמיים של האוניברסיטאות היוקרתיות ביותר בעולם. הצרה היא שכמעט כולם נושרים בדרך ובממוצע מדהים ומבייש - רק 5% מאלו שהתחילו קורס כזה מסיימים אותו...
נחזור אלינו. אוסף הסרטונים של אלי נצר "שיעורטון" מציע לימוד מתמטיקה לתיכון בצורה קלה וידידותית. אלי, מורה למתמטיקה בתיכון בתל אביב, שילב את המילים שיעור וסרטון ויוצר בכל נושא סרטון קצר שמסביר ומלמד בקלות את הבעיה.
היתרונות של הלימוד עם הסרטונים הללו הוא שכל אחד יכול ללמוד את הנושא שהוא צריך, בזמן, בקצב ובמקום המתאים לו.
באתר "שיעורטון" יש מגוון ענק של שיעורטונים מתמטיים. הללו מסודרים וממויינים לפי תוכניות הלימוד ושאלוני הבגרות השונים.
הצפייה בסרטונים היא לגמרי בחינם. הלומדים יוכלו למצוא בכל דף שאלון גם פתרונות מלאים לשאלות הבגרות במתמטיקה, כשהם ממויינים לפי נושאים. כול הכבוד אלי!
הנה המורה שמלמד מתמטיקה באמצעות סרטוני לימוד מקוונים, אלי נצר (עברית):
https://youtu.be/En9Iv-I1Gbc

סטטיסטיקה היא תחום ידע שבו אוספים ומנתחים מידע כמותי, כדי להסיק מסקנות. כך למשל אוספים נתונים על אזרחי המדינה ומנתחים אותם וכך לומדים על חייהם, עיסוקיהם, מצבם הכלכלי ועוד. או שאוספים את נתוני הקליעה של שחקני כדורסל ואחרי ניתוח מגיעים למסקנות על הבולטים שבהם ואלו שעושים עבודה פחות טובה.
הסטטיסטיקה נחשבת מדע שאינו ניסויי, אך היא משרתת היטב את אנשי המדע. הסטטיסטיקאים משתמשים בכלים מתמטיים כדי לטפל בנתונים שלקוחים במרבית המקרים מהתחומים המדעיים של מדעי הטבע ומדעי החברה ומסייעים לגלות בהם דברים חשובים, שיכולים לתרום מאד.
אך לסטטיסטיקה יש גם מגבלות לא קטנות. למשל בכך שהיא עובדת טוב על מספרים גדולים ודי רע על מספרים קטנים. לדוגמה, הבה נביט על אדם שרגלו האחת בגיגית מים רותחים ורגלו השנייה בגיגית של מים קפואים. על פי הסטטיסטיקה יהיה מצבו טוב, שכן ממוצע החום שבין המים הרותחים והמים הקפואים יהיה נורמלי. עם זאת, ברור לנו שבמציאות אדם כזה יסבול מאד... אולי משום כך היה מי שהעיד שאמר פעם בנג'מין ד'יזראלי, ראש ממשלת בריטניה, "יש שלושה סוגי שקרים: שקרים, שקרים גסים וסטטיסטיקה"...
דוגמה נוספת לבעיה של הסטטיסטיקה היא היכולת לנבא ממדגם קטן על האוכלוסיה כולה. למשל, לא פעם חוזים הסוקרים הפוליטיים את תוצאות הבחירות. הם עושים זאת בעזרת מדגם (קבוצה קטנה שאמורה לייצג את האוכלוסיה כולה). אך לא פעם, עם פרסום תוצאות האמת, מסתבר שהם טעו. ברוב המקרים הסיבה לכך היא שסטטיסטיקה היא מנבא מוגבל ולא תמיד מדויק של המציאות.
הנה דוגמאות קטנות למסקנות מעולם הסטטיסטיקה (עברית):
https://youtu.be/o4oM-7UOYRQ
סרטון שמדגים כמה שסטטיסטיקה יכולה להטעות כשמבינים ממנה דברים לא נכונים (עברית):
http://youtu.be/cKHAfiqHwZc
הסבירות הגדולה שסטטיסטיקה תטעה (מתורגם):
https://youtu.be/sxYrzzy3cq8
והסטודנטים לסטטיסטיקה באוניברסיטה (עברית):
https://youtu.be/b-k13rnRFcU

האם שאלתם את עצמכם פעם למה כדאי ללמוד מתמטיקה? - אם היה לכם ספק, אולי תסייע לכם האגדה שמסופרת בצורות שונות על ממציא משחק השחמט שהוזמן אל קיסר סין. הקיסר שאל מה ירצה כאות תודה על המשחק המופלא. לממציא השחמט הייתה בקשה מוזרה ודי צנועה: תן לי גרגרי אורז על משבצות לוח השחמט, כשבכל משבצת יש כמות כפולה של גרגרים מהקודמת לה - גרגיר אורז על המשבצת הראשונה, שני גרגירים על השנייה, ארבעה במשבצת השלישית וכן הלאה.
הקיסר, שהתרגל לבקשות גדולות יותר, שאל אם זה כל מה שירצה והממציא השיב לו בצניעות שדי לו בגרגירי האורז שביקש. "כמה טיפש יכול אדם להיות..." חשב ודאי הקיסר והסכים לבקשתו.
אבל מה גדול היה ההבדל שבין הקיסר הבור והממציא החכם. כל בעל ידע בסיסי במתימטיקה יזהה בחישוביו שהכמות של האורז שתונח על לוח השחמט היא בלתי נתפסת וגדלה באופן אקספוננציאלי, דוגמה מצוינת לגידול מעריכי בחשבון - מגרגר אחד ושני גרגרים במשבצות הראשונות תגדל הכמות לקילוגרם אורז במשבצת ה-15, טון אורז במשבצת ה-25, 1000 טון במשבצת ה-35 וכך הלאה.. במשבצת ה-55 יונח כל יבול האורז השנתי של העולם כולו ובמשבצת האחרונה תצטרך להיות כמות אורז שהיא גדולה מכל האורז שגדל אי-פעם בתולדות האדם!
אז אם יש לכם תכניות להמציא משהו גאוני והשליט שלכם הוא נדיב במיוחד, אולי כדאי לשקוד על לימודי המתמטיקה.
#דיון בכמות האורז
חישוב שקיבלנו ממשתמש אאוריקה מציע הסתייגות מתמטית מעניינת. הנה דבריו:
"קילוגרם אורז מכיל 45,000 גרגרים בממוצע. היבול השנתי של האורז בעולם הוא 700 מליון טון בממוצע של העשור האחרון. שהם 31.5E15 גרגרים.
הפרס הנדרש הוא 2^64, שזה סיכום של כל חזקות שתיים מאפס ועד 63. = 18.4E18
סך כל הפרס שווה ל-585 שנות גידול אורז. בהנחה שגידול האורז עלה עם השנים, ניתן להניח שכמות האורז שגדלה בששת אלפים שנות קיום העולם תספיק לממציא שלנו..."
אנו שואלים אתכם האם לדעתכם הכמות השנתית של ימינו היא זהה לכמות השנתית בעולם לפני אלף, אלפיים וששת אלפים שנה?"
הנה סרטון שמספר על אגדת האורז ולוח השחמט:
http://youtu.be/t3d0Y-JpRRg
וסרטון נוסף שמסביר את הסיפור במונחים החשבוניים של הגדילה המעריכית:
http://youtu.be/D9DvjkMMULw

הפילוסוף, הפיזיקאי והמתמטיקאי הצרפתי בְּלֶז פסקל (Blaise Pascal) המציא למעשה את המחשב המכני הראשון בהיסטוריה. מכונת החישוב שבנה בשנת 1642 היא המחשב הראשון שידע לבצע פעולות חשבוניות כלשהן.
במשך כ-15 שנים מחייו בנה בלייז פסקאל מכונות חישוב שונות. היום מכנים אותן מכונות החישוב של פסקל (Pascal's calculators) והן הלכו והשתכללו. אולם "המחשב של פסקל", או "הפסקלין" כמו שקראו לו מאוחר יותר, נחשב באותה תקופה לגימיק או לאטרקציה בידורית.
למעט הממציא, איש לא התייחס למכונת החישוב שלו ברצינות מספקת. אולי זה משום שלא היה לה שימוש של ממש. ואגב, גם לשימוש מסחרי היא הייתה יקרה מדי.
מכונת החישוב של פסקאל, שנבנו ממנה כ-50 יחידות בלבד, ביצעה פעולות חשבוניות פשוטות כמו חיבור וחיסור. היא אפילו ידעה להעביר ספרות מושאלות - ספרות שיעברו לעשיריה הבאה, ממש כמו בתרגילים כתובים, מעמודה לעמודה.
במהלך השנים הבאות תשוכלל הפסקלין על ידי המתמטיקאי הגרמני גוטפריד לייבניץ, שיוסיף לה את האפשרות לפעולת הכפל.
כך פעלה מכונת החישוב של בלייז פסקאל:
http://youtu.be/3h71HAJWnVU
וקיצור חייו של בלז פסקאל:
https://youtu.be/IDMdnJDN1f4
מתמטיקה

הפאי הוא מספר אי רציונאלי, מציין את היחס בין היקף מעגל לקוטרו. זהו מספר מסתורי, שמתמטיקאים וחובבי מתמטיקה מוקסמים ממנו כבר דורות רבים. ערכו של פאי שווה בקירוב ל 3.14.
הפאי מסומן באות היוונית π. הבבלים, ממציאי הגלגל, גילו אותו כבר לפני ששת אלפים שנה. התגלית של התופעה המרתקת של פאי, הייתה שבכל גודל מעגל שהוא, תוצאת החילוק של היקף המעגל ברדיוס שלו תהיה תמיד אותו המספר. 4000 שנה אחריהם, הצליחו מדעני מצרים העתיקה להגיע לערך מקורב של פאי. ארכימדס היווני הציג לראשונה, כבר במאה ה-3 לפני הספירה, שיטה שמאפשרת לאמוד את π.
הראשון שהצליח לחשב את פיי בדיוק גבוה היה אויילר. פיתוח החשבון הדיפרנציאלי והאינטגרלי סייע לו מאד והוא חישב את פאי עד 153 ספרות אחרי הנקודה. כמו הרבה דברים שאויילר תרם למתמטיקה, הוא גם זה שהעניק לפיי את שמו.
כיום, בעידן המחשב, המתמטיקאים עובדים על אלגוריתמים ונוסחאות אלגנטיות לחישוב פאי. השיא שנקבע עד 2011 הוא של 10 טריליון ספרות אחרי הנקודה!
הנה סרטון על משמעותו של הפיי (מתורגם):
http://youtu.be/9a5vHXsUvUw?t=13s
שיר לימודי באנגלית, להיכרות עם חישוב פאי:
http://youtu.be/eiHWHT_8WrE
מלחין שהחליט להלחין את המספר וכך לזכור אותו:
https://youtu.be/wM-x3pUcdeo
והביטוי המוסיקלי של המספר פאי ויחס הזהב שבנוי עליו:
https://youtu.be/9mozmHgg9Sk?long=yes

אם ניקח שטרות כסף עשויי נייר ונניח אותם זה על זה, כשכל פעם אנו מכפילים את מספר השטרות שלפנינו פי שניים, נקבל כבר אחרי 42 הכפלות הר של שטרות, כה גבוה עד שיגיע מפני הקרקע של כדור הארץ ועד לירח - מרחק מדהים של 380 אלף קילומטרים!
המספר המדהים הזה נובע מהגידול המעריכי (Exponential growth) של מספר השטרות.
גידול מעריכי, גדילה אקספוננציאלית, גדילה מעריכית, צמיחה מעריכית, גידול גאומטרי, טור גאומטרי ועוד הרבה שמות דומים - כולם מייצגים קצב גידול תלול במיוחד, שגדל בהכפלות ומשום כך הוא מהיר במיוחד.
לגידול האקספוננציאלי יש דוגמאות רבות בטבע. מסתבר שאם לא יאיימו עליהם מחלות או טורפים, תגדל אוכלוסיית החיידקים גדילה מעריכית, שתחדול לגדול רק כשייגמרו חומרי המזון על פני כדור הארץ, או שתורעל מחומרי הפסולת שהיא תשאיר אחריה.
באופן דומה יגדלו בגידול אקספוננציאלי גם אוכלוסיות של וירוסים שאין מולם חיסון (כמו שגילינו בהתפשטות המהירה של וירוס הקורונה), בשמרים שהם פטריות ומתפתחים במהירות ובחרקים שבבית הגידול שלהם יש מזון ואין איום עליהם.
גם בני אדם משתמשים בצמיחה מעריכית שכזו, במיזמים אנושיים שונים. "חוק מור" למשל, קבע שמהירות המחשבים מוכפלת כל שנה וחצי, מה שהופך את מהירותם לצומחת צמיחה אקספוננציאלית. כך גם מתנהגת ריבית דריבית, שנותנת החזר מעריכי למלווים, בתנאי כמובן שהתנאים נשארים קבועים, כולל שער הריבית.
משווקים בשיווק רב-שכבתי, כמו גם נוכלים ב"תרמיות פונזי" וב"משחקי פירמידה" - גם הם בונים את העיסקה על כך שכל מצטרף מגייס מספר אנשים, שיגייסו כל אחד כמה אחרים וכך הלאה. כך צומחת ההכנסה של כל משתתף, לא רק מרווחיו שלו, אלא גם מהמתגייסים שיצטרפו במורד השרשרת שמתחתיו - מגוייסיו, מגוייסיהם וכל מי שיגויס בהמשך.
בפיסיקה התגלה שבתגובת שרשרת גרעינית, שהיא הבסיס לכלי נשק גרעיני, פוגע כל גרעין אורניום שעבר ביקוע גרעיני, בגרעינים אחרים וגורם לביקועם, מה שיגרום לכל אחד מהם לפגוע בגרעינים אחרים ולבקעם וחוזר חלילה. אז אתם כבר יודעים איזו גדילה זו שיוצרת את הפיצוץ הנורא הזה - גדילה מעריכית, או בלעז: גידול אקספוננציאלי.
הנה סרטון שמדגים את הגדילה המעריכית (מתורגם):
https://youtu.be/AmFMJC45f1Q
התחזית של מלתוס מסוף המאה ה-19 על התפוצצות עתידית של אוכלוסיית העולם:
http://youtu.be/vZVOU5bfHrM
הכלכלה - האם היא תצמח לנצח?
https://youtu.be/mT3P0YSNonE
הסבר מתמטי (עברית):
https://youtu.be/6HsnjP0NzfE
יש מי שמסביר בעזרת הצמיחה המעריכית מדוע כדאי לבנות מסגרות פוליטיות "ללא כוכבים" (עברית):
https://youtu.be/Exg6ZdUpvkw
ושיעור באקדמיית קאן על גדילה מעריכית (עברית):
https://youtu.be/VZTDP9MvqLw?long=yes

כנער במאה ה-17, שרצה לבלות זמן רב יותר עם אביו העסוק בחישובי מיסים עבור מלך צרפת, הוא המציא מכונת חישוב מכנית שתקל על אביו את החישובים החשבוניים ותפנה לו זמן לשחק איתו - עם בנו, בלז פסקל (Blaise Pascal).
ואכן, גם כשגדל היה הצרפתי בְּלֶז פסקל איש מדע רב-תחומי פעיל ומבריק. הוא פעל כמתמטיקאי, פיזיקאי ופילוסוף. מי שכבר מילדותו התעניין במספרים ובחשבון, הצליח ללמד את עצמו את חוקי הגאומטריה ומצא פתרונות מקוריים לבעיות גאומטריות שחלקן העסיקו מתמטיקאים מבוגרים. כמי שהחל מוקדם, הוא גם מת מוקדם. בגיל 39 הוא סיים את חייו, ובכל זאת הספיק לא מעט.
פסקל השתמש בכל כשרונו המתמטי כדי לבנות את מכונת החישוב המכאנית, אולי הראשונה בהיסטוריה - מכונת ה"פסקלין". המכונה שפיתח כדי לסייע בחישובי המס של אביו, נציב מס מטעם המלך, הייתה גאונית לזמנה וידעה לבצע פעולות חיבור וחיסור באמצעות גלגלי שיניים.
במאה ה-20 ידעו ראשוני המחשב להוקיר אותו כשקראו על שמו את שפת התכנות "פסקל".
אבל פסקל המגוון לא עסק רק במכונות חישוב שהקדימו את זמנן. הוא גם ניסח את הבסיס לתורת ההסתברות, ביחד עם המתמטיקאי פרמה. תורת ההסתברות שיצרו השניים היא מיסודות המדע המודרני.
הנה קצת על פסקל:
https://youtu.be/vu0nVuntD7g
סיפורו של פסקל:
https://youtu.be/xTaAx-f8mW8
סרטון על חייו:
https://youtu.be/IDMdnJDN1f4
הסבר המשולש של פסקל (ללא מילים):
http://youtu.be/YUqHdxxdbyM
והביוגרפיה המורחבת מעט של פסקל:
https://youtu.be/Tu1xNSEemuc

מהו הניסוי המתמטי במשטח נייר עם צד אחד בלבד?
האם אפשר ליצור משטח נייר עם צד אחד בלבד?
הנה ניסוי מדהים שמראה איך המתמטיקה היא דבר שאפשר להרגיש בידיים וכמה שהיא מופלאה. כל מה שצריך הוא פיסת נייר ארוכה ונייר דבק.
הנה סרטון עם ניסוי ליצירת רצועת מביוס בעצמך (עברית):
http://youtu.be/EaG4_EgIZPE
האם אפשר ליצור משטח נייר עם צד אחד בלבד?
הנה ניסוי מדהים שמראה איך המתמטיקה היא דבר שאפשר להרגיש בידיים וכמה שהיא מופלאה. כל מה שצריך הוא פיסת נייר ארוכה ונייר דבק.
הנה סרטון עם ניסוי ליצירת רצועת מביוס בעצמך (עברית):
http://youtu.be/EaG4_EgIZPE

מספר המנגינות האפשריות הוא עצום, אבל ראשית כדאי שנקבע מה האורך שאנו רוצים לבדוק. אם מנגינה היא בת 8 צלילים, הרי שניתן לחבר כמעט 80 מיליארד מנגינות כאלה, מבלי לחזור על עצמן. אם תרצו לדעת את המספר המדויק של המנגינות האפשריות באורך כזה, במרווחים של 12 חצאי טונים בסולם, מדובר ב-78,364,164,096 אפשרויות בדיוק.
אז האם אין כמעט סיכוי שמנגינות יהיו כל כך דומות לאחרות? - אז זהו, שלא פעם זה קורה ואנחנו שמים לב ששירים מזכירים שירים אחרים שאנו מכירים.
התשובה היא תבניות. על אף שלכאורה יש לנו ביליוני אפשרויות של מנגינות שניתן לחבר, אנחנו נוטים לחבר מנגינות דומות ומוסיקה דומה לזו שכבר יש ושממנה אנו נהנים. אנחנו נוטים להשתמש בתבניות מוכרות לנו, כי אלה תבניות שאנו מתחברים אליהן תרבותית, מוסיקלית, מראש. הרי אם נכתוב שיר רוק, הרי שככל הנראה אנו חובבי רוק ומכירים שירי רוק, כך שמראש השיר יהיה בסגנון ועם מאגר ההשפעות "הרוקיות" ששמענו בעבר. לפעמים עלולות להיות בדמיון הזה אפילו היבטים משפטיים, של הפרת זכויות יוצרים.
כמובן שיש אנשים שנוטים יותר אל המוכר, גם אם לא במודע, ויש מקוריים יותר, פורצי דרך, אנשים שגם כשהם פועלים בסגנון מסוגלים להמציא לחנים מעניינים ומקוריים יותר. אבל זה כבר הבדל בין אנשים, יכולתם הקוגניטיבית והיצירתית ולא מתמטיקה. כי כמו "חוק העדר" שמושך את מרבית האנשים, מבלי שהם שמים לב לכך, להיצמד לאנשים, למשל על חוף ים ענקי וריק, ולא ללכת לשבת רחוק מכולם, כך גם כאן - מרבית המלחינים לא באמת יתרחקו מ"המוכר והטוב", מבחינתם.
הנה סרטון ארוך שמסביר את העניין בצורה מעניינת ורחבה אף יותר:
https://youtu.be/DAcjV60RnRw?long=yes
שימו לב לתבנית הרמונית בת 4 אקורדים, שמשמשת שוב ושוב לכתיבה של אינספור להיטי ענק:
https://youtu.be/oOlDewpCfZQ
איך פתר אוילר את חידת גשרי קניגסברג?
המתמטיקאי החשוב ביותר של המאה ה-18 היה לאונרד אוֹילֶר השווייצרי, שאת רוב חייו בילה ברוסיה ובגרמניה. עם 886 ספרים ומאמרים שפרסם בחייו, רובם בשנים שבהן סבל מעיוורון ולמעשה התעוור לחלוטין.
הוא נחשב מהפוריים שבמתמטיקאים והפורה ביותר בבני דורו.
אוילר תרם תרומה מכרעת לתחומים רבים ומגוונים במתמטיקה. הוא גם היה זה שהכניס לשימוש סימנים מתמטיים רבים שמקובלים כיום, כמו למשל, בקביעת האות היוונית פיי לסימון היחס בין הקף של מעגל לקוטר שלו.
אוילר הוא גם המייסד של תורת הגרפים, שחשיבותה בחייו לא נראתה אולי גדולה מדי, אך בעידן המודרני יש לגרפים חשיבות רבה. כמעט אי-אפשר לראות התנהלות מדעית, הנדסית וכלכלית ללא הגרפים שמציגים רעיונות ותהליכים כל כך טוב.
חידת גשרי קניגסברג היא חידה שבה יש מערכת גשרים (בעיר אמיתית, אגב) שבה רצה אוילר למצוא מסלול שעובר בכל הגשרים ופעם אחת בלבד בכל גשר. זו נשמעת חידה סתמית אבל מדובר במתמטיקה והוא היה המתמטיקאי שפתר אותה.
הנה סרטון שמציג את בעיית גשרי קניגסברג (מתורגם):
https://youtu.be/nZwSo4vfw6c
קביעתו החכמה של אוילר לגבי פתרונה (עברית):
http://youtu.be/-LqxT1SMgR0?t=3m13s
יצוג מוסרט של בעיית הגשרים של קניגסברג:
http://youtu.be/2qBZ1-9VuLA
וסרטון קצר על לאונרד אוילר:
http://youtu.be/Ty6ejK1rAkg
המתמטיקאי החשוב ביותר של המאה ה-18 היה לאונרד אוֹילֶר השווייצרי, שאת רוב חייו בילה ברוסיה ובגרמניה. עם 886 ספרים ומאמרים שפרסם בחייו, רובם בשנים שבהן סבל מעיוורון ולמעשה התעוור לחלוטין.
הוא נחשב מהפוריים שבמתמטיקאים והפורה ביותר בבני דורו.
אוילר תרם תרומה מכרעת לתחומים רבים ומגוונים במתמטיקה. הוא גם היה זה שהכניס לשימוש סימנים מתמטיים רבים שמקובלים כיום, כמו למשל, בקביעת האות היוונית פיי לסימון היחס בין הקף של מעגל לקוטר שלו.
אוילר הוא גם המייסד של תורת הגרפים, שחשיבותה בחייו לא נראתה אולי גדולה מדי, אך בעידן המודרני יש לגרפים חשיבות רבה. כמעט אי-אפשר לראות התנהלות מדעית, הנדסית וכלכלית ללא הגרפים שמציגים רעיונות ותהליכים כל כך טוב.
חידת גשרי קניגסברג היא חידה שבה יש מערכת גשרים (בעיר אמיתית, אגב) שבה רצה אוילר למצוא מסלול שעובר בכל הגשרים ופעם אחת בלבד בכל גשר. זו נשמעת חידה סתמית אבל מדובר במתמטיקה והוא היה המתמטיקאי שפתר אותה.
הנה סרטון שמציג את בעיית גשרי קניגסברג (מתורגם):
https://youtu.be/nZwSo4vfw6c
קביעתו החכמה של אוילר לגבי פתרונה (עברית):
http://youtu.be/-LqxT1SMgR0?t=3m13s
יצוג מוסרט של בעיית הגשרים של קניגסברג:
http://youtu.be/2qBZ1-9VuLA
וסרטון קצר על לאונרד אוילר:
http://youtu.be/Ty6ejK1rAkg
מי היה פייר דה פרמה?
פייר דה פרמה היה כנראה גדול חובבי המתמטיקה. הוא היה בכלל עורך דין ובמתמטיקה הוא עסק בתור תחביב. פרמה התפרסם בזכות עבודתו בתורת המספרים. בעיקר זכור "משפט פרמה" שטוען כי למשוואה מסוימת אין פתרונות שלמים שאינם אפס עבור המשתנים שלה. מתמטיקאים רבים ניסו במהלך השנים להוכיח את המשפט ורק בשנת 1994 הוא הוכח סופית.
פרמה ובלז פסקל הם שהניחו את היסודות לתורת ההסתברות. פרמה גם הניח עקרון בסיסי באופטיקה גיאומטרית, שקובע שהאור בוחר במסלול המהיר ביותר.
הנה סרטון על פרמה:
http://youtu.be/Ij01HGgxnkA
ותיאור ויזואלי למשפט האחרון של פרמה:
http://youtu.be/xG63O03lWZI
פייר דה פרמה היה כנראה גדול חובבי המתמטיקה. הוא היה בכלל עורך דין ובמתמטיקה הוא עסק בתור תחביב. פרמה התפרסם בזכות עבודתו בתורת המספרים. בעיקר זכור "משפט פרמה" שטוען כי למשוואה מסוימת אין פתרונות שלמים שאינם אפס עבור המשתנים שלה. מתמטיקאים רבים ניסו במהלך השנים להוכיח את המשפט ורק בשנת 1994 הוא הוכח סופית.
פרמה ובלז פסקל הם שהניחו את היסודות לתורת ההסתברות. פרמה גם הניח עקרון בסיסי באופטיקה גיאומטרית, שקובע שהאור בוחר במסלול המהיר ביותר.
הנה סרטון על פרמה:
http://youtu.be/Ij01HGgxnkA
ותיאור ויזואלי למשפט האחרון של פרמה:
http://youtu.be/xG63O03lWZI
מה מקורו של סמל האינסוף?
סמל האינסוף הוא ∞. הוא נראה כ"ספרה 8 שוכבת" ולהיסטוריונים לא ברור מדוע הוא נבחר לייצג את מושג האינסוף החמקמק כל כך.
אולי משום כך הוא פופולרי בתרבות המערבית ורק לאחרונה בחרה פייסבוק בסמל הזה לייצג את Meta, החברה החדשה שתנהל את כל הטכנולוגיה שלה.
נראה שהסמל נבחר במאה ה-17, על ידי המתמטיקאי האנגלי ג'ון ואליס, שעסק בפיתוח החשבון הדיפרנציאלי והאינטגראלי.
מקור הרעיון לסמל זה לא ברור. אולי צורת הספרות הרומיות העתיקות CIƆ, שמסמנות את המספר 1000 שמשמעותו בתרבות הרומית "הרבה". סברה אחרת קושרת אותו לאות היוונית האחרונה, שסמל האינסוף מזכיר - אומגה ω. אחרים טוענים שצורת סמל האינסוף מזכירה את טבעת מביוס שאינה נגמרת (ראו באאוריקה בתגית "טבעת מביוס") והיא גם זו שנתנה לו את השם הלטיני "למינסקוס" (lemniscus) שפירושו רצועה.
יש גם הקושרים את סימן האינסוף לסמל הפגאני (האלילי) העתיק אורובורוס (Ouroboros), שהוא הנחש הבולע את זנבו. בתרבויות רבות סימן סמל האורובורוס מחזוריות אינסופית, שאומרת שהכל חוזר שוב ושוב ושום דבר לא מסתיים, אלא מתחיל מחדש..
אין סרטון על סמל האינסוף אז תירגעו:
http://youtu.be/zj4azK2DcK4
הרצאונת על האינסוף והסמל שלו:
http://youtu.be/mXnP7CtvC-A
כינוס שלם בנושא:
http://youtu.be/KDCJZ81PwVM
ומסתבר שסמל האינסוף הוא אמצעי מצויין להירגע:
http://youtu.be/cn7559OzYEs
סמל האינסוף הוא ∞. הוא נראה כ"ספרה 8 שוכבת" ולהיסטוריונים לא ברור מדוע הוא נבחר לייצג את מושג האינסוף החמקמק כל כך.
אולי משום כך הוא פופולרי בתרבות המערבית ורק לאחרונה בחרה פייסבוק בסמל הזה לייצג את Meta, החברה החדשה שתנהל את כל הטכנולוגיה שלה.
נראה שהסמל נבחר במאה ה-17, על ידי המתמטיקאי האנגלי ג'ון ואליס, שעסק בפיתוח החשבון הדיפרנציאלי והאינטגראלי.
מקור הרעיון לסמל זה לא ברור. אולי צורת הספרות הרומיות העתיקות CIƆ, שמסמנות את המספר 1000 שמשמעותו בתרבות הרומית "הרבה". סברה אחרת קושרת אותו לאות היוונית האחרונה, שסמל האינסוף מזכיר - אומגה ω. אחרים טוענים שצורת סמל האינסוף מזכירה את טבעת מביוס שאינה נגמרת (ראו באאוריקה בתגית "טבעת מביוס") והיא גם זו שנתנה לו את השם הלטיני "למינסקוס" (lemniscus) שפירושו רצועה.
יש גם הקושרים את סימן האינסוף לסמל הפגאני (האלילי) העתיק אורובורוס (Ouroboros), שהוא הנחש הבולע את זנבו. בתרבויות רבות סימן סמל האורובורוס מחזוריות אינסופית, שאומרת שהכל חוזר שוב ושוב ושום דבר לא מסתיים, אלא מתחיל מחדש..
אין סרטון על סמל האינסוף אז תירגעו:
http://youtu.be/zj4azK2DcK4
הרצאונת על האינסוף והסמל שלו:
http://youtu.be/mXnP7CtvC-A
כינוס שלם בנושא:
http://youtu.be/KDCJZ81PwVM
ומסתבר שסמל האינסוף הוא אמצעי מצויין להירגע:
http://youtu.be/cn7559OzYEs
מי המתמטיקאי שהראה את חוסר השלמות של המתמטיקה?
הלוגיקן והמתמטיקאי יליד אוסטריה, קורט גדל, היה גאון ומגדולי הלוגיקאים. רבים רואים בו את גדול הלוגיקאים מאז אריסטו. התגלית הגדולה בקריירה שלו הייתה צמד "משפטי אי השלמות של גדל". בתפיסה כמעט רוחנית, הוא הצליח לחשוף בעיה שאין לה פתרון בהשלטת שיטה בחשיבה המתימטית. גדל ראה בכך הוכחה לקיומה של אמת נצחית, שבן האנוש יכול לתפוס רק את הקצה שלה, מבלי יכולת להכילה.
גדל היה גם חבר קרוב ביותר של אלברט איינשטיין בסוף חייו. על אף גאונותו, הוא נחשב תמהוני וסבל מפראנויה. זוהי מחלת נפש שגם תביא למותו, כתוצאה מתת-תזונה שנבעה מחשש שמנסים להרעילו ושהביאה לכך שהפסיק לאכול לחלוטין.
הנה סרטון קצר על תיאוריית חוסר השלמות של גדל:
http://youtu.be/xjT6x8yZvpY
וקורט גדל, מי שכונה הלוגיקן הגדול ביותר מאז אריסטו:
http://youtu.be/B2DY8WvSOLU?t=21s
הלוגיקן והמתמטיקאי יליד אוסטריה, קורט גדל, היה גאון ומגדולי הלוגיקאים. רבים רואים בו את גדול הלוגיקאים מאז אריסטו. התגלית הגדולה בקריירה שלו הייתה צמד "משפטי אי השלמות של גדל". בתפיסה כמעט רוחנית, הוא הצליח לחשוף בעיה שאין לה פתרון בהשלטת שיטה בחשיבה המתימטית. גדל ראה בכך הוכחה לקיומה של אמת נצחית, שבן האנוש יכול לתפוס רק את הקצה שלה, מבלי יכולת להכילה.
גדל היה גם חבר קרוב ביותר של אלברט איינשטיין בסוף חייו. על אף גאונותו, הוא נחשב תמהוני וסבל מפראנויה. זוהי מחלת נפש שגם תביא למותו, כתוצאה מתת-תזונה שנבעה מחשש שמנסים להרעילו ושהביאה לכך שהפסיק לאכול לחלוטין.
הנה סרטון קצר על תיאוריית חוסר השלמות של גדל:
http://youtu.be/xjT6x8yZvpY
וקורט גדל, מי שכונה הלוגיקן הגדול ביותר מאז אריסטו:
http://youtu.be/B2DY8WvSOLU?t=21s
מהי רקורסיה?
רקורסיה היא הליך שפונה לעצמו. קצת יותר מורכב הוא ההסבר או המיקוד של בעיה כללית אל בעיה "קטנה" יותר, אך זהה לבעיה המקורית.
לפיכך, גם הגדרה רקורסיבית היא הגדרה שחייבת לפנות לאותה הגדרה, אבל בתנאים שונים. ותמיד יהיה שם תנאי עצירה, כדי שהרקורסיה לא תהיה אינסופית..
הגדרה אחרת לרקורסיה היא "הגדרת בעיה במונחים של עצמה".
רוצים דוגמה:
"אם הבנת מהי רקורסיה, חזור אל הדף ממנו הגעת. אם לא – קרא בדף זה מהי רקורסיה".
הדוגמה הזו מסבירה בדיוק את הרקורסיה, כי תנאי העצירה הוא "אם הבנת.." ,בעוד ש"אם לא" אז חוזרים לאותה דוגמה כדי ללמוד מהי רקורסיה מחדש ולבסוף מבינים שהרקורסיה היא מה שאתה מתבקש לעשות...
#בתכנות
מתכנתים משתמשים הרבה ברקורסיה. הם מתארים פונקציה רקורסיבית כ"פונקציה שקוראת לעצמה". נכון היה יותר לומר שפונקציה כזו קוראת לעותק של עצמה אבל בכל מקרה הפונקציה הזו קוראת לעצמה בלולאה (Loop) עד שלא ניתן יותר לעשות זאת - כלומר, יש תנאי יציאה שמבטיח שהיא לא תעשה את זה עד אינסוף ויהיה stack overflow...
לרוב נותנים לרקורסיה כזו את הדוגמה של חישוב n-עצרת במתמטיקה (=מכפלת 1 כפול 2 כפול 3… עד כפול n).
ואגב, הנה משפט נכון ומשעשע, אחד הממים השנונים של האינטרנט הגיקי: "כדי להגדיר רקורסיה, קודם-כל צריך להגדיר רקורסיה.."
הנה הסבר יפה לרקורסיה עם דוגמה קולנועית:
https://youtu.be/Q83nN97LVOU
סרטון שמדגים איך רקורסיה עובדת כשעושים בעזרתה גרפיקה ממוחשבת:
http://youtu.be/ghZKKaZkzrE
כניסה פנימה לפרקטל - צורה גרפית שנקראת "משולש סירפינסקי" ונבנתה בפונקציה רקורסיבית:
http://youtu.be/P5EkdJRtF-4
בקצרה:
https://youtu.be/rf60MejMz3E
והסבר למתכנתים (עברית):
https://youtu.be/B19qH3XFnxY?long=yes
רקורסיה היא הליך שפונה לעצמו. קצת יותר מורכב הוא ההסבר או המיקוד של בעיה כללית אל בעיה "קטנה" יותר, אך זהה לבעיה המקורית.
לפיכך, גם הגדרה רקורסיבית היא הגדרה שחייבת לפנות לאותה הגדרה, אבל בתנאים שונים. ותמיד יהיה שם תנאי עצירה, כדי שהרקורסיה לא תהיה אינסופית..
הגדרה אחרת לרקורסיה היא "הגדרת בעיה במונחים של עצמה".
רוצים דוגמה:
"אם הבנת מהי רקורסיה, חזור אל הדף ממנו הגעת. אם לא – קרא בדף זה מהי רקורסיה".
הדוגמה הזו מסבירה בדיוק את הרקורסיה, כי תנאי העצירה הוא "אם הבנת.." ,בעוד ש"אם לא" אז חוזרים לאותה דוגמה כדי ללמוד מהי רקורסיה מחדש ולבסוף מבינים שהרקורסיה היא מה שאתה מתבקש לעשות...
#בתכנות
מתכנתים משתמשים הרבה ברקורסיה. הם מתארים פונקציה רקורסיבית כ"פונקציה שקוראת לעצמה". נכון היה יותר לומר שפונקציה כזו קוראת לעותק של עצמה אבל בכל מקרה הפונקציה הזו קוראת לעצמה בלולאה (Loop) עד שלא ניתן יותר לעשות זאת - כלומר, יש תנאי יציאה שמבטיח שהיא לא תעשה את זה עד אינסוף ויהיה stack overflow...
לרוב נותנים לרקורסיה כזו את הדוגמה של חישוב n-עצרת במתמטיקה (=מכפלת 1 כפול 2 כפול 3… עד כפול n).
ואגב, הנה משפט נכון ומשעשע, אחד הממים השנונים של האינטרנט הגיקי: "כדי להגדיר רקורסיה, קודם-כל צריך להגדיר רקורסיה.."
הנה הסבר יפה לרקורסיה עם דוגמה קולנועית:
https://youtu.be/Q83nN97LVOU
סרטון שמדגים איך רקורסיה עובדת כשעושים בעזרתה גרפיקה ממוחשבת:
http://youtu.be/ghZKKaZkzrE
כניסה פנימה לפרקטל - צורה גרפית שנקראת "משולש סירפינסקי" ונבנתה בפונקציה רקורסיבית:
http://youtu.be/P5EkdJRtF-4
בקצרה:
https://youtu.be/rf60MejMz3E
והסבר למתכנתים (עברית):
https://youtu.be/B19qH3XFnxY?long=yes
איך מחשבים ספרת ביקורת בתעודת זהות?
ספרת ביקורת בתעודת זהות נועדה למנוע שגיאות בכתיבת המספר. כן, בניגוד למה שרבים חושבים, אין לה כלל תפקיד של אבטחה.
לחישוב ספרת הביקורת משתמשים באלגוריתם שנקרא אלגוריתם לוהן (Luhn), על שמו של איש מעבדות IBM בשנות ה-50 שפיתח אותו.
החישוב הוא זה: הימנית מתשע ספרות של מספר הזהות בישראל היא ספרת הביקורת.
לכל אחת משמונה הספרות הראשונות נותנים משקל - כל ספרה זוגית מוכפלת ואי זוגית לא. כלומר, המשקל יהיה 1 (לספרה ראשונה), 2, 1, 2, 1, 2, 1, 2.
מכפילים כל ספרה במשקל שלה ואז מחברים את כל הספרות של התוצאות יחדיו. אגב, שימו לב שאם התוצאה של הכפלת הספרה במשקלה היא בת שתי ספרות, מסכמים כל אחת משתי הספרות של התוצאה בנפרד. 12 למשל, תחובר כ-1 ואחריו 2.
את הסכום שמתקבל משלימים לכפולה הקרובה של 10, כלפי מעלה. אם הסכום שהתקבל הוא 34 למשל, ההשלמה תהיה ל-40 ולכן היא 6. זוהי ספרת הביקורת.
אז זהו. כך מחברים את ספרת הביקורת במספר תעודת הזהות שלכם. אגב, ספרת ביקורת יש גם במספר של כרטיס אשראי, מספרי ברקוד ובמספר חשבון הבנק שלכם.
הנה חישוב של מספר כרטיס אשראי (זהה לת"ז):
https://youtu.be/Yr9s5NjsVAo
ושל ספרת ביקורת בברקוד:
https://youtu.be/4C3uwfoR88c
ספרת ביקורת בתעודת זהות נועדה למנוע שגיאות בכתיבת המספר. כן, בניגוד למה שרבים חושבים, אין לה כלל תפקיד של אבטחה.
לחישוב ספרת הביקורת משתמשים באלגוריתם שנקרא אלגוריתם לוהן (Luhn), על שמו של איש מעבדות IBM בשנות ה-50 שפיתח אותו.
החישוב הוא זה: הימנית מתשע ספרות של מספר הזהות בישראל היא ספרת הביקורת.
לכל אחת משמונה הספרות הראשונות נותנים משקל - כל ספרה זוגית מוכפלת ואי זוגית לא. כלומר, המשקל יהיה 1 (לספרה ראשונה), 2, 1, 2, 1, 2, 1, 2.
מכפילים כל ספרה במשקל שלה ואז מחברים את כל הספרות של התוצאות יחדיו. אגב, שימו לב שאם התוצאה של הכפלת הספרה במשקלה היא בת שתי ספרות, מסכמים כל אחת משתי הספרות של התוצאה בנפרד. 12 למשל, תחובר כ-1 ואחריו 2.
את הסכום שמתקבל משלימים לכפולה הקרובה של 10, כלפי מעלה. אם הסכום שהתקבל הוא 34 למשל, ההשלמה תהיה ל-40 ולכן היא 6. זוהי ספרת הביקורת.
אז זהו. כך מחברים את ספרת הביקורת במספר תעודת הזהות שלכם. אגב, ספרת ביקורת יש גם במספר של כרטיס אשראי, מספרי ברקוד ובמספר חשבון הבנק שלכם.
הנה חישוב של מספר כרטיס אשראי (זהה לת"ז):
https://youtu.be/Yr9s5NjsVAo
ושל ספרת ביקורת בברקוד:
https://youtu.be/4C3uwfoR88c
איך ארטוסתנס גילה את קוטר כדור הארץ ואת המספרים הראשוניים?
המתמטיקאי, הגאוגרף והאסטרונום היווני אֵרָטוֹסְתֶנֶס (Eratosthenes), שחי במאה השלישית לפני הספירה, חי את רוב חייו באלכסנדריה שבמצרים. שם הוא היה הספרן הראשי ומי שניהל את הספרייה הגדולה של אלכסנדריה.
בין השגיו המדעיים נחשבת השיטה למציאת כל המספרים הראשוניים. לשם כך הוא פיתח את "הנפה של ארטוסתנס" - אלגוריתם פשוט ויעיל למציאת כל המספרים הראשוניים עד למספר שלם מסוים.
אבל ארטוסתנס נודע במיוחד בהישגו החשוב ביותר - מדידת ההיקף של כדור הארץ. בעזרת מקל פשוט ואינטליגנציה מופלאה, הוא הצליח לדייק בסטיה של 15% בלבד מההיקף האמיתי של כדור הארץ.
זוהי רמת דיוק מצוינת לתקופתו. בחישובים שלו התעלה ארטוסתנס במשך מאות שנים על חוקרים שכשלו בכך. שיטתו נחשבת למדויקת אף מזו של תלמי, האסטרונום החשוב ביותר בעת העתיקה, ש-500 שנה אחריו, חישב את היקף כדור-הארץ באופן שגוי.
כך גילה ארתוסטנס את קוטר כדור הארץ (מתורגם):
http://youtu.be/F8UFGu2M2gM?t=1m25s
שלב אחרי שלב, הנה הדרך בה חוקר הגאון את היקף כדור הארץ:
https://youtu.be/EfZ2HZH5CkA
קרל סאגאן האגדי מספר עליו באלכסנדריה:
https://youtu.be/G8cbIWMv0rI
ומדע הגיאודזיה שנולד מתגליתו של ארטוסתנס (מתורגם):
http://youtu.be/wKzhaTFmS5w
המתמטיקאי, הגאוגרף והאסטרונום היווני אֵרָטוֹסְתֶנֶס (Eratosthenes), שחי במאה השלישית לפני הספירה, חי את רוב חייו באלכסנדריה שבמצרים. שם הוא היה הספרן הראשי ומי שניהל את הספרייה הגדולה של אלכסנדריה.
בין השגיו המדעיים נחשבת השיטה למציאת כל המספרים הראשוניים. לשם כך הוא פיתח את "הנפה של ארטוסתנס" - אלגוריתם פשוט ויעיל למציאת כל המספרים הראשוניים עד למספר שלם מסוים.
אבל ארטוסתנס נודע במיוחד בהישגו החשוב ביותר - מדידת ההיקף של כדור הארץ. בעזרת מקל פשוט ואינטליגנציה מופלאה, הוא הצליח לדייק בסטיה של 15% בלבד מההיקף האמיתי של כדור הארץ.
זוהי רמת דיוק מצוינת לתקופתו. בחישובים שלו התעלה ארטוסתנס במשך מאות שנים על חוקרים שכשלו בכך. שיטתו נחשבת למדויקת אף מזו של תלמי, האסטרונום החשוב ביותר בעת העתיקה, ש-500 שנה אחריו, חישב את היקף כדור-הארץ באופן שגוי.
כך גילה ארתוסטנס את קוטר כדור הארץ (מתורגם):
http://youtu.be/F8UFGu2M2gM?t=1m25s
שלב אחרי שלב, הנה הדרך בה חוקר הגאון את היקף כדור הארץ:
https://youtu.be/EfZ2HZH5CkA
קרל סאגאן האגדי מספר עליו באלכסנדריה:
https://youtu.be/G8cbIWMv0rI
ומדע הגיאודזיה שנולד מתגליתו של ארטוסתנס (מתורגם):
http://youtu.be/wKzhaTFmS5w
מהי בעיית מונטי הול?
זו אחת החידות המתמטיות המפורסמות בעולם, שמקורה בתורת המשחקים ויש לה הסבר סטטיסטי די פשוט, אבל רבים מתקשים לקבל ולהבין אותו והוא נתפס אצלם כפרדוקסלי ונוגד את ההיגיון.
בעיית "מונטי הול" (Monty Hall problem) היא בעיה מפורסמת בתורת ההסתברות, שפתרונה אינו אינטואיטיבי, כלומר סותר את האינטואיציה שלנו (ההיגיון העממי).
החידה, שיש הקוראים לה "הפרדוקס של מונטי הול", מבוססת על שעשועון טלוויזיה אמריקאי פופולרי משנות ה-60 שנקרא "Let's Make a Deal".
שמו של מנחה התכנית היה מונטי הול והוא גילם את תפקיד המנחה הערמומי בהצלחה כה רבה, שהבעיה נקראת על שמו. ואגב, הבעיה היא ממש לא חדשה ומקורה עוד במאה ה-19 כשבסוף שנות ה-50 פרסם אותה מחדש מרטין גרדנר.
בישראל קראו לתכנית הטלוויזיה הזו "עשינו עסק" ומכאן שיש המכנים אותה "בעיית עשינו עסק".
#מה הבעיה?
נציג את הבעיה באופן כזה:
ישנן 3 דלתות סגורות. מאחורי אחת מהן יש פרס יקר ערך, בדרך כלל מכונית, ומאחורי שתי האחרות יש עזים. מן הסתם הן גם לא נוסעות טוב וערכן גם נמוך צזה של מכונית.
המשתתף, או "השחקן" בשעשועון, בוחר באקראי דלת אחת. לאחר שבחר, פותח המנחה, שיודע מה מסתתר מאחורי כל דלת, דלת אחרת שבה בוודאות יש עז.
עכשיו, משנפתחה דלת עם עז, מקבל השחקן את האפשרות לשנות את בחירתו ולבחור בדלת הנותרת הסגורה במקום בדלת שבחר בה בתחילה.
וכאן נשאלת השאלה המרכזית: האם כדאי לו לשנות את הבחירה?
זו דילמה. התלבטות. האם כדאי לו? - כדי שלא תישארו במתח נאמר מיד שכן.
כדאי לו לשנות את בחירתו, מכיוון ש:
- בהתחלה הסיכוי שהמכונית מאחורי הדלת שבחרת הוא 1/3.
- הסיכוי שהמכונית מאחורי אחת מהדלתות האחרות הוא 2/3.
- כשהמנחה פותח דלת עם עז ומאפשר לשחקן לבחור שוב, הסיכוי שהמכונית נמצאת מאחורי הדלת שלא נבחרה וטרם נפתחה הוא 2/3.
וזו בדיוק הסיבה שהעברת הבחירה לדלת השנייה מגדילה את סיכוייו לזכות במכונית מסיכוי של 1/3 לסיכוי טוב יותר - של 2/3.
#הסבר
הבעיה מבהירה כיצד הידע הנוסף של המנחה (הידיעה מה מאחורי הדלתות) משנה את ההסתברויות, וזה לא אינטואיטיבי בהתחלה. אם נחשב את האפשרויות עם מספר גדול של דלתות (למשל 1,000 דלתות), יהיה קל לראות שהחלפת הבחירה כמעט תמיד מביאה להצלחה.
כך שברור שברוב המקרים כדאי לשנות את הבחירה לאחר שהמנחה חושף דלת עם עז.
#אנקדוטה היסטורית
מי שאחראית לפרסום של הבעיה היא בעלת הטור האמריקאית מרילין ווס סוונט (Vos Savant), מי שלפי ספר השיאים של גינס נחשבה לבעלת ה-IQ הגבוה ביותר בעולם.
בטור השאלות והתשובות שלה סוונט התייחסה לבעיית מונטי הול וגם נתנה לה את הפתרון הנכון, שאומר שעדיף להחליף את הבחירה. בימים שאחרי הפרסום והתקיפו אותה המוני קוראים, אלפים שלעגו ומיהרו להוקיע אותה, על מה שהם הגדירו כ“טעות”. ביניהם היו גם מספר מתמטיקאים מכובדים.
כמובן שבסוף הסתבר שהיא צדקה ומי שטעו הם דווקא הלועגים. במהלך השנים, אגב, הופיע הספר “המקרה המוזר של הכלב בשעת לילה”, בו תוארה התנפלות הקןראים עליה וצוטטו אמירות מתוך חלק מאותם מכתבים נזעמים שהם שלחו לה.
הנה דילמת מונטי הול (עברית):
https://youtu.be/4stFDiXWuYk
במה תבחרו? (מתורגם)
https://youtu.be/9vRUxbzJZ9Y
סיפורו של שעשועון הטלוויזיה הזה:
https://youtu.be/4Lb-6rxZxx0
הסבר של פרדוקס מונטי הול (עברית):
https://youtu.be/I4dlT9s2zP8
ודוגמה לפתרון מעולם הסרטים (מתורגם):
https://youtu.be/Q5nCtgcL4jU
את העניין הזה מלמדים בקורסים לסטטיסטיקה (עברית):
https://youtu.be/m6S91Uh7rEg?long=yes
זו אחת החידות המתמטיות המפורסמות בעולם, שמקורה בתורת המשחקים ויש לה הסבר סטטיסטי די פשוט, אבל רבים מתקשים לקבל ולהבין אותו והוא נתפס אצלם כפרדוקסלי ונוגד את ההיגיון.
בעיית "מונטי הול" (Monty Hall problem) היא בעיה מפורסמת בתורת ההסתברות, שפתרונה אינו אינטואיטיבי, כלומר סותר את האינטואיציה שלנו (ההיגיון העממי).
החידה, שיש הקוראים לה "הפרדוקס של מונטי הול", מבוססת על שעשועון טלוויזיה אמריקאי פופולרי משנות ה-60 שנקרא "Let's Make a Deal".
שמו של מנחה התכנית היה מונטי הול והוא גילם את תפקיד המנחה הערמומי בהצלחה כה רבה, שהבעיה נקראת על שמו. ואגב, הבעיה היא ממש לא חדשה ומקורה עוד במאה ה-19 כשבסוף שנות ה-50 פרסם אותה מחדש מרטין גרדנר.
בישראל קראו לתכנית הטלוויזיה הזו "עשינו עסק" ומכאן שיש המכנים אותה "בעיית עשינו עסק".
#מה הבעיה?
נציג את הבעיה באופן כזה:
ישנן 3 דלתות סגורות. מאחורי אחת מהן יש פרס יקר ערך, בדרך כלל מכונית, ומאחורי שתי האחרות יש עזים. מן הסתם הן גם לא נוסעות טוב וערכן גם נמוך צזה של מכונית.
המשתתף, או "השחקן" בשעשועון, בוחר באקראי דלת אחת. לאחר שבחר, פותח המנחה, שיודע מה מסתתר מאחורי כל דלת, דלת אחרת שבה בוודאות יש עז.
עכשיו, משנפתחה דלת עם עז, מקבל השחקן את האפשרות לשנות את בחירתו ולבחור בדלת הנותרת הסגורה במקום בדלת שבחר בה בתחילה.
וכאן נשאלת השאלה המרכזית: האם כדאי לו לשנות את הבחירה?
זו דילמה. התלבטות. האם כדאי לו? - כדי שלא תישארו במתח נאמר מיד שכן.
כדאי לו לשנות את בחירתו, מכיוון ש:
- בהתחלה הסיכוי שהמכונית מאחורי הדלת שבחרת הוא 1/3.
- הסיכוי שהמכונית מאחורי אחת מהדלתות האחרות הוא 2/3.
- כשהמנחה פותח דלת עם עז ומאפשר לשחקן לבחור שוב, הסיכוי שהמכונית נמצאת מאחורי הדלת שלא נבחרה וטרם נפתחה הוא 2/3.
וזו בדיוק הסיבה שהעברת הבחירה לדלת השנייה מגדילה את סיכוייו לזכות במכונית מסיכוי של 1/3 לסיכוי טוב יותר - של 2/3.
#הסבר
הבעיה מבהירה כיצד הידע הנוסף של המנחה (הידיעה מה מאחורי הדלתות) משנה את ההסתברויות, וזה לא אינטואיטיבי בהתחלה. אם נחשב את האפשרויות עם מספר גדול של דלתות (למשל 1,000 דלתות), יהיה קל לראות שהחלפת הבחירה כמעט תמיד מביאה להצלחה.
כך שברור שברוב המקרים כדאי לשנות את הבחירה לאחר שהמנחה חושף דלת עם עז.
#אנקדוטה היסטורית
מי שאחראית לפרסום של הבעיה היא בעלת הטור האמריקאית מרילין ווס סוונט (Vos Savant), מי שלפי ספר השיאים של גינס נחשבה לבעלת ה-IQ הגבוה ביותר בעולם.
בטור השאלות והתשובות שלה סוונט התייחסה לבעיית מונטי הול וגם נתנה לה את הפתרון הנכון, שאומר שעדיף להחליף את הבחירה. בימים שאחרי הפרסום והתקיפו אותה המוני קוראים, אלפים שלעגו ומיהרו להוקיע אותה, על מה שהם הגדירו כ“טעות”. ביניהם היו גם מספר מתמטיקאים מכובדים.
כמובן שבסוף הסתבר שהיא צדקה ומי שטעו הם דווקא הלועגים. במהלך השנים, אגב, הופיע הספר “המקרה המוזר של הכלב בשעת לילה”, בו תוארה התנפלות הקןראים עליה וצוטטו אמירות מתוך חלק מאותם מכתבים נזעמים שהם שלחו לה.
הנה דילמת מונטי הול (עברית):
https://youtu.be/4stFDiXWuYk
במה תבחרו? (מתורגם)
https://youtu.be/9vRUxbzJZ9Y
סיפורו של שעשועון הטלוויזיה הזה:
https://youtu.be/4Lb-6rxZxx0
הסבר של פרדוקס מונטי הול (עברית):
https://youtu.be/I4dlT9s2zP8
ודוגמה לפתרון מעולם הסרטים (מתורגם):
https://youtu.be/Q5nCtgcL4jU
את העניין הזה מלמדים בקורסים לסטטיסטיקה (עברית):
https://youtu.be/m6S91Uh7rEg?long=yes
מהו המספר גוגול?
לא שחסרים מספרים גדולים במתמטיקה, אבל המפורסם שבמספרים הגדולים הוא ללא ספק הגוגול (Googol). גוגול הוא המספר שהיה ההשראה לשם שבחרו מקימי חברת האינטרנט גוגל, אחת החברות המצליחות בכל הזמנים, לחברה שהקימו. אבל אפילו הרווחים האדירים של חברת האינטרנט "גוגל" לא מתקרבים אליו.. גוגול הוא 10100 (10 בחזקת 100) והוא נכתב כ-1 עם מאה אפסים.
השם "גוגול" הוצע למספר העצום על ידי האחיין בן ה-9 של המתמטיקאי אדוארד קסנר. קסנר רצה להמחיש מספר גדול באמת לתלמידי המתמטיקה שלו ונדרש לשם "חיבה" בשבילו. הוא הצליח - כיום כל תלמיד מתמטיקה מכיר אותו.
רוצים לדעת כמה גדול הוא הגוגול? - דמיינו שאם נספור את כל האטומים הקיימים ביקום כולו המספר גוגול עדיין יהיה גדול מהם, זאת מכיוון שעל פי הערכות המדענים מספר האטומים שביקום כולו הוא כ- 1080
מיד אחרי שקנסר ואחיינו הגדירו את הגוגל הם הגדירו גם את המספר גוגלפלקס (Googolplex). המוגדר כספרה 1 ואחריה Googol אפסים. ניתן להציג אותו בצורה מתמטית גם כך 10googol או כך 10 (10100).
הנה המדען הגאון קרל סגן מראה בצורה ברורה כמה עצום גודלם של המספרים גוגול וגוגולפלקס:
https://youtu.be/0lFQOmb6mVs
עוד סרטון על המספרים גוגול וגוגולפלקס:
https://youtu.be/8GEebx72-qs
ואפשר פשוט לשיר את גוגול והוא יירשם מעצמו:
https://youtu.be/5JOAoiX1LHA
לא שחסרים מספרים גדולים במתמטיקה, אבל המפורסם שבמספרים הגדולים הוא ללא ספק הגוגול (Googol). גוגול הוא המספר שהיה ההשראה לשם שבחרו מקימי חברת האינטרנט גוגל, אחת החברות המצליחות בכל הזמנים, לחברה שהקימו. אבל אפילו הרווחים האדירים של חברת האינטרנט "גוגל" לא מתקרבים אליו.. גוגול הוא 10100 (10 בחזקת 100) והוא נכתב כ-1 עם מאה אפסים.
השם "גוגול" הוצע למספר העצום על ידי האחיין בן ה-9 של המתמטיקאי אדוארד קסנר. קסנר רצה להמחיש מספר גדול באמת לתלמידי המתמטיקה שלו ונדרש לשם "חיבה" בשבילו. הוא הצליח - כיום כל תלמיד מתמטיקה מכיר אותו.
רוצים לדעת כמה גדול הוא הגוגול? - דמיינו שאם נספור את כל האטומים הקיימים ביקום כולו המספר גוגול עדיין יהיה גדול מהם, זאת מכיוון שעל פי הערכות המדענים מספר האטומים שביקום כולו הוא כ- 1080
מיד אחרי שקנסר ואחיינו הגדירו את הגוגל הם הגדירו גם את המספר גוגלפלקס (Googolplex). המוגדר כספרה 1 ואחריה Googol אפסים. ניתן להציג אותו בצורה מתמטית גם כך 10googol או כך 10 (10100).
הנה המדען הגאון קרל סגן מראה בצורה ברורה כמה עצום גודלם של המספרים גוגול וגוגולפלקס:
https://youtu.be/0lFQOmb6mVs
עוד סרטון על המספרים גוגול וגוגולפלקס:
https://youtu.be/8GEebx72-qs
ואפשר פשוט לשיר את גוגול והוא יירשם מעצמו:
https://youtu.be/5JOAoiX1LHA
מהם מגדלי האנוי?
מגדלי האנוי הם שם של חידה מפורסמת שהומצאה על ידי המתמטיקאי הצרפתי אדוארד לוקאס בשנת 1883. ב"מגדלי הנוי" נתון מגדל עם דיסקיות שהיקפן הולך ונעשה קטן ככל שהן עליונות (הרחבות למטה). מטרת החידה היא להעביר את כל המגדל בשלמותו לאחד משני העמודים הריקים שלידו. כמובן שיש להעביר את הדיסקיות במה שפחות צעדים וכמה שיותר מהר.
החידה משמשת ללימוד מתמטיקה ומדעי המחשב ולהמחשת מושגים כמו רקורסיה (ראו באאוריקה בתגית "רקורסיה"). עוד פרט מעניין - אם נסמן בנקודה כל מצב חוקי במשחק מגדלי האנוי, ונקשר בקווים את המצבים שבהם אפשר לעבור מאחד לשני, נקבל למול עינינו את גרף המשחק, בצורה של הפרקטל המוכר כ"משולש שרפינסקי".
אגב, לוקאס המציא גם אגדה שמדובר במקדש בראהמי שבו הכהנים מעבירים מגדל בן 64 דיסקיות. על פי האגדה שלו, כשיסיימו הכהנים את עבודתם, יגיע גם סוף העולם..
ישנם כללים להעברה:
א. בכל שלב תעבור רק דיסקית אחת מקום.
ב. אסור שיהיה מצב שדיסקית תהיה מונחת על דיסקית קטנה יותר.
הנה דרך לפתרון של חידת מגדלי האנוי:
http://youtu.be/BMkOBNZHcIs
מגדלי האנוי הם שם של חידה מפורסמת שהומצאה על ידי המתמטיקאי הצרפתי אדוארד לוקאס בשנת 1883. ב"מגדלי הנוי" נתון מגדל עם דיסקיות שהיקפן הולך ונעשה קטן ככל שהן עליונות (הרחבות למטה). מטרת החידה היא להעביר את כל המגדל בשלמותו לאחד משני העמודים הריקים שלידו. כמובן שיש להעביר את הדיסקיות במה שפחות צעדים וכמה שיותר מהר.
החידה משמשת ללימוד מתמטיקה ומדעי המחשב ולהמחשת מושגים כמו רקורסיה (ראו באאוריקה בתגית "רקורסיה"). עוד פרט מעניין - אם נסמן בנקודה כל מצב חוקי במשחק מגדלי האנוי, ונקשר בקווים את המצבים שבהם אפשר לעבור מאחד לשני, נקבל למול עינינו את גרף המשחק, בצורה של הפרקטל המוכר כ"משולש שרפינסקי".
אגב, לוקאס המציא גם אגדה שמדובר במקדש בראהמי שבו הכהנים מעבירים מגדל בן 64 דיסקיות. על פי האגדה שלו, כשיסיימו הכהנים את עבודתם, יגיע גם סוף העולם..
ישנם כללים להעברה:
א. בכל שלב תעבור רק דיסקית אחת מקום.
ב. אסור שיהיה מצב שדיסקית תהיה מונחת על דיסקית קטנה יותר.
הנה דרך לפתרון של חידת מגדלי האנוי:
http://youtu.be/BMkOBNZHcIs
מהו משולש סירפינסקי?
משולש שרפינסקי, שנקרא גם ספוג שרפינסקי או משולש סירפינסקי, הוא אחד הפרקטלים המפורסמים. את ההיכרות עימו עשו המתמטיקאים בשנת 1915. המשולש קיבל את שמו מהמתמטיקאי הפולני שתיאר אותו לראשונה, ואצלב שרפינסקי.
משולש שרפינסקי הוא דוגמה מצוינת ופשוטה במיוחד לפרקטל, צורה שמורכבת מעותקים מוקטנים של עצמה, עד אינסוף. הוא בנוי משלושה עותקים שלו שהוקטנו בחצי שוב ושוב.
הנה משולש סרפינסקי שלא נגמר, להדגמת הרקורסיה הפשוטה:
http://youtu.be/QsMvoui5WlQ?t=10s
סרט אפל מתורגם ומדהים על הפרקטלים ומשולש שרפינסקי בתוכם (מתורגם):
https://youtu.be/0C75vRVL5lE
סרטון בגרפיקת מחשב של "משולש סירפינסקי" שנבנה ברקורסיה בתלת-מימד:
http://youtu.be/P5EkdJRtF-4
משולש שרפינסקי מסוכריות של החג הנוצרי המעט מפחיד "ליל כל הקדושים":
http://youtu.be/z8ZWlUamNPI
וכך יוצרים פרקטלים כמו משולש סרפינסקי:
http://youtu.be/XwWyTts06tU?t=1m22s
משולש שרפינסקי, שנקרא גם ספוג שרפינסקי או משולש סירפינסקי, הוא אחד הפרקטלים המפורסמים. את ההיכרות עימו עשו המתמטיקאים בשנת 1915. המשולש קיבל את שמו מהמתמטיקאי הפולני שתיאר אותו לראשונה, ואצלב שרפינסקי.
משולש שרפינסקי הוא דוגמה מצוינת ופשוטה במיוחד לפרקטל, צורה שמורכבת מעותקים מוקטנים של עצמה, עד אינסוף. הוא בנוי משלושה עותקים שלו שהוקטנו בחצי שוב ושוב.
הנה משולש סרפינסקי שלא נגמר, להדגמת הרקורסיה הפשוטה:
http://youtu.be/QsMvoui5WlQ?t=10s
סרט אפל מתורגם ומדהים על הפרקטלים ומשולש שרפינסקי בתוכם (מתורגם):
https://youtu.be/0C75vRVL5lE
סרטון בגרפיקת מחשב של "משולש סירפינסקי" שנבנה ברקורסיה בתלת-מימד:
http://youtu.be/P5EkdJRtF-4
משולש שרפינסקי מסוכריות של החג הנוצרי המעט מפחיד "ליל כל הקדושים":
http://youtu.be/z8ZWlUamNPI
וכך יוצרים פרקטלים כמו משולש סרפינסקי:
http://youtu.be/XwWyTts06tU?t=1m22s
מהי הסתברות?
אי-ודאות היא אחד הדברים שמלווים אותנו בחיים. לא פעם אנו חשים בחוסר וודאות, מכיוון שאין לנו יכולת לחזות את מזג האוויר, תוצאות של אירועי ספורט, או תוצאות של בחירות. למצבים כאלו יש כלי שיכול לסייע - הִסְתַּבְּרוּת (Probability).
הסתברות היא מושג מתמטי שמבטא את הסבירות שמאורע מסוים יתרחש. לעיתים יש לנו מושג מה סביר שיקרה, גם אם איננו יודעים בודאות מה יקרה. תורת ההסתברות מכמתת את "הסביר" ומודדת אותו באופן מדויק.
מדידת הסתברות של מאורע מסוים היא בסקאלה שבין 0 ל־1. מאורע בלתי אפשרי מקבל הסתברות 0, בעוד הסתברות 1 ניתנת למאורע שיש ודאות מוחלטת שיקרה. לעיתים קורה שמשתמשים באחוזים, בין 0% ל־100%, כדי לבטא הסתברות.
כשאנו מטילים מטבע, ההסתברות שהוא יפול על צד מסוים שלו היא 0.5, כלומר שבממוצע המטבע תיפול על אותו צד באחת מכל שתי זריקות. באופן דומה, ההסתברות שהכדור ברולטה ייפול על כל אחד מהמספרים, היא שווה.
היסטורית יש להסתברות עבר ארוך. עוד במאה ה-16 עסקו בחישובי הסתברויות. מאז הלך הענף הזה במתמטיקה והתפתח, כשהשימוש בו מסייע בתחומי הכלכלה, העסקים, ההימורים ועוד.
כך למשל קובעות חברות ביטוח את מחיר ביטוח החיים על פי ההסתברות שהמבוטח ייפגע או ימות במהלך תקופת הביטוח. חזאי מזג אוויר בוחנים את ההסתברות לגשם, בכדי להציע תחזית אמינה.
גם מהמרים נעזרים בחישובים כדי לדעת את הסיכויים שיזכו בהגרלות או במשחקים וכך הלאה.
הנה הדרך שבה ניתן לראות הסתברות (מתורגם):
https://youtu.be/Kgudt4PXs28
הדגמת ההסתברות דרך ניחושים (מתורגם):
https://youtu.be/3V2omKRX9gc
בעיית מונטי הול מדגימה יפה את ההסתברות וכמה שאינה אינטואיטיבית (עברית):
https://youtu.be/4stFDiXWuYk
מה ההסתברות לזכות בפיס כלומר בלוטו (עברית)?
https://youtu.be/_vyjrgU7hng
ודוגמה להסתברות שנוגדת את האינטואיציה שלנו (מתורגם):
https://youtu.be/Ghbkv0MKV-w
אי-ודאות היא אחד הדברים שמלווים אותנו בחיים. לא פעם אנו חשים בחוסר וודאות, מכיוון שאין לנו יכולת לחזות את מזג האוויר, תוצאות של אירועי ספורט, או תוצאות של בחירות. למצבים כאלו יש כלי שיכול לסייע - הִסְתַּבְּרוּת (Probability).
הסתברות היא מושג מתמטי שמבטא את הסבירות שמאורע מסוים יתרחש. לעיתים יש לנו מושג מה סביר שיקרה, גם אם איננו יודעים בודאות מה יקרה. תורת ההסתברות מכמתת את "הסביר" ומודדת אותו באופן מדויק.
מדידת הסתברות של מאורע מסוים היא בסקאלה שבין 0 ל־1. מאורע בלתי אפשרי מקבל הסתברות 0, בעוד הסתברות 1 ניתנת למאורע שיש ודאות מוחלטת שיקרה. לעיתים קורה שמשתמשים באחוזים, בין 0% ל־100%, כדי לבטא הסתברות.
כשאנו מטילים מטבע, ההסתברות שהוא יפול על צד מסוים שלו היא 0.5, כלומר שבממוצע המטבע תיפול על אותו צד באחת מכל שתי זריקות. באופן דומה, ההסתברות שהכדור ברולטה ייפול על כל אחד מהמספרים, היא שווה.
היסטורית יש להסתברות עבר ארוך. עוד במאה ה-16 עסקו בחישובי הסתברויות. מאז הלך הענף הזה במתמטיקה והתפתח, כשהשימוש בו מסייע בתחומי הכלכלה, העסקים, ההימורים ועוד.
כך למשל קובעות חברות ביטוח את מחיר ביטוח החיים על פי ההסתברות שהמבוטח ייפגע או ימות במהלך תקופת הביטוח. חזאי מזג אוויר בוחנים את ההסתברות לגשם, בכדי להציע תחזית אמינה.
גם מהמרים נעזרים בחישובים כדי לדעת את הסיכויים שיזכו בהגרלות או במשחקים וכך הלאה.
הנה הדרך שבה ניתן לראות הסתברות (מתורגם):
https://youtu.be/Kgudt4PXs28
הדגמת ההסתברות דרך ניחושים (מתורגם):
https://youtu.be/3V2omKRX9gc
בעיית מונטי הול מדגימה יפה את ההסתברות וכמה שאינה אינטואיטיבית (עברית):
https://youtu.be/4stFDiXWuYk
מה ההסתברות לזכות בפיס כלומר בלוטו (עברית)?
https://youtu.be/_vyjrgU7hng
ודוגמה להסתברות שנוגדת את האינטואיציה שלנו (מתורגם):
https://youtu.be/Ghbkv0MKV-w
