מה גילה בנואה מנדלברוט?
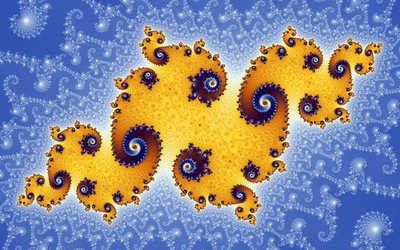
בנואה מנדלברוט היה מתמטיקאי שמצא שיש צורות רבות שכל חלק שלהן הוא כמו השלם, או מזכיר אותו. מדידה של שטח הפנים של צורות כאלה תלוייה ביכולת שלנו לבחון אותו, מכיוון שככל שנתקרב אל העצם, נגלה חספוס הולך וגובר, שיגדיל את שטח הפנים.
מנדלברוט מצא שכלל מתמטי פשוט, או נוסחה פשוטה, יכולים להגדיר מצוין את העצם שנראה שאין בו חוקיות או היגיון כלשהם.
אגב, בנואה מנדלברוט עצמו מעדיף את המונח "חספוס" ולא אי-יציבות או אי-סדר, מכיוון שהוא רואה סדר בכל דבר ואין בעיניו שום דבר שאין בו סדר מסוים. להוכחה, המילה "פרקטל" שהוא בחר לתיאור של המחוספס והשבור באה מהמילה הלטינית פרקטוס (fractus), שפירושה "שבור".
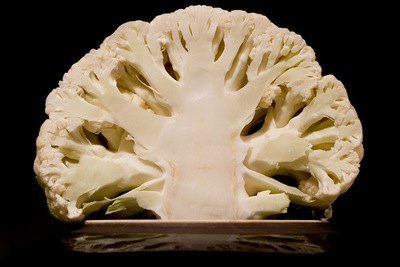
למשל בכרובית הוא רואה גם תחכום וגם פשטות. אותם קונוסים שאנו רואים בברוקולי, חוזרים גם אם נביט בחלק מקונוס כזה ויחזרו שוב ושוב בכל קנה מידה שנביט בו. כך יהיה גם בעננים, בקווי חוף עם מפרצים בגדלים (מפיורדים עצומים ועד מפרצונים בגוגל מילימטרים), עצים (בהם עורקי העלה נראים כענפים וענפי העץ דומים לעצים) ועוד המון צורות שהן לכאורה אקראיות ולא בנויות בסדר של ממש, אבל כשנביט בחלק מהם נראה בגדלים שונים, תבנית דומה לזו שראינו בעצם המלא.
איך זה מסתדר? - ובכן, בכולם יש מרכיב שניתן למצוא והוא "הדמיון העצמי" (Self similarity), שבו אותה צורה חוזרת שוב ושוב, ככל שנתקרב. ומסתבר שאותה צורה שבה ענפים יוצאים מענפים בעץ, היא גם הצורה של צינורות הדם בגופנו, נימי העלים של העץ, נהרות על פני כדור הארץ וכן הלאה. מסתבר שהטבע עושה שימוש בחוק זהה להמון מקרים שאינם קשורים זה בזה ושכביכול אין בהם שום סדר הגיוני.
ל"דמיון העצמי" מנדלברוט קרא "פרקטל". הוא גם הבין שניתן לעבוד עם הפרקטלים הפוך ולהשתמש בסדרה של חוקים מתמטיים פשוטים, כדי לייצר צורות כאלה. בסוף שנות ה-50 הוא השתמש במחשב כדי לייצר צורות כאלה. הוא עשה מהפכה של ממש בגאומטריה, שכן הוא החל לקרב אותה לעולם הטבע.
אם קודם לפרקטלים לא סייעה הגאומטריה לתאר את הצורות של גורמים בטבע, כמו הרים, עננים, עצים, ירקות וקווי חוף, הרי שהפרקטל, שמסייע למצוא סדר בדפוסים מורכבים ביותר, שינה את זה והראה את הסדר המתמטי שבו מתנהל הטבע והעולם הכאוטי. או במילים שלו כפי שכתב בהקדמת ספרו "עננים הם לא כדורים, הרים אינם בעלי צורה של חרוט, קו החוף לא עשוי ממעגלים, קליפת העץ איננה חלקה והברק אינו מתקדם בקו ישר".
בחייו סבל מנדלברוט לא מעט בשל הפרקטלים. הממסד המתמטי ממש נידה אותו בשל ההתעסקות בתמונות, שלא יאה למתמטיקאי רציני. מי שהצילה אותו מחוסר תעסוקה הייתה חברת IBM, שלא זו בלבד שהעסיקה אותו במרכז המחקר שלה, אלא אף נתנה לו לעשות כרצונו. בעזרת חוק רקורסיבי פשוט מאוד הוא מצליח עתה לייצר תמונות בעלות מורכבות הולכת וגדלה, בה רואים ברמות שונות, כאמור, צורות דומות.
גם הציבור הרחב מתחיל להתחבר לרעיונות שלו, שבניגוד לרעיונות מתמטיים רגילים, קל להבינם. מה עוד שניתן היה לראותם לפתע, בתוצרי מחשב מודפסים. את הצד הגרפי של הפרקטלים ניתן היה גם לחקור וליישם באדריכלות, בעיצוב מוצר ובתעשיות שונות.
וכך זוכה מי שכילד בן 12 הפך לפליט פולני בצרפת ולימד את עצמו מתמטיקה לבדו, הוא זוכה בשלב מסוים בציבור לכינוי "כוכב הרוק של המתמטיקה". כי גם אם רעיונותיו על הפרקטלים עדיין לא מתקבלים אצל הקהילה המדעית, מעל ראשם הוא הופך די מהר לאחד המתמטיקאים המשפיעים בהיסטוריה.
בנואה מנדלברוט היה מתמטיקאי שמצא שיש צורות רבות שכל חלק שלהן הוא כמו השלם, או מזכיר אותו. מדידה של שטח הפנים של צורות כאלה תלוייה ביכולת שלנו לבחון אותו, מכיוון שככל שנתקרב אל העצם, נגלה חספוס הולך וגובר, שיגדיל את שטח הפנים.
מנדלברוט מצא שכלל מתמטי פשוט, או נוסחה פשוטה, יכולים להגדיר מצוין את העצם שנראה שאין בו חוקיות או היגיון כלשהם.
אגב, בנואה מנדלברוט עצמו מעדיף את המונח "חספוס" ולא אי-יציבות או אי-סדר, מכיוון שהוא רואה סדר בכל דבר ואין בעיניו שום דבר שאין בו סדר מסוים. להוכחה, המילה "פרקטל" שהוא בחר לתיאור של המחוספס והשבור באה מהמילה הלטינית פרקטוס (fractus), שפירושה "שבור".
למשל בכרובית הוא רואה גם תחכום וגם פשטות. אותם קונוסים שאנו רואים בברוקולי, חוזרים גם אם נביט בחלק מקונוס כזה ויחזרו שוב ושוב בכל קנה מידה שנביט בו. כך יהיה גם בעננים, בקווי חוף עם מפרצים בגדלים (מפיורדים עצומים ועד מפרצונים בגוגל מילימטרים), עצים (בהם עורקי העלה נראים כענפים וענפי העץ דומים לעצים) ועוד המון צורות שהן לכאורה אקראיות ולא בנויות בסדר של ממש, אבל כשנביט בחלק מהם נראה בגדלים שונים, תבנית דומה לזו שראינו בעצם המלא.
איך זה מסתדר? - ובכן, בכולם יש מרכיב שניתן למצוא והוא "הדמיון העצמי" (Self similarity), שבו אותה צורה חוזרת שוב ושוב, ככל שנתקרב. ומסתבר שאותה צורה שבה ענפים יוצאים מענפים בעץ, היא גם הצורה של צינורות הדם בגופנו, נימי העלים של העץ, נהרות על פני כדור הארץ וכן הלאה. מסתבר שהטבע עושה שימוש בחוק זהה להמון מקרים שאינם קשורים זה בזה ושכביכול אין בהם שום סדר הגיוני.
ל"דמיון העצמי" מנדלברוט קרא "פרקטל". הוא גם הבין שניתן לעבוד עם הפרקטלים הפוך ולהשתמש בסדרה של חוקים מתמטיים פשוטים, כדי לייצר צורות כאלה. בסוף שנות ה-50 הוא השתמש במחשב כדי לייצר צורות כאלה. הוא עשה מהפכה של ממש בגאומטריה, שכן הוא החל לקרב אותה לעולם הטבע.
אם קודם לפרקטלים לא סייעה הגאומטריה לתאר את הצורות של גורמים בטבע, כמו הרים, עננים, עצים, ירקות וקווי חוף, הרי שהפרקטל, שמסייע למצוא סדר בדפוסים מורכבים ביותר, שינה את זה והראה את הסדר המתמטי שבו מתנהל הטבע והעולם הכאוטי. או במילים שלו כפי שכתב בהקדמת ספרו "עננים הם לא כדורים, הרים אינם בעלי צורה של חרוט, קו החוף לא עשוי ממעגלים, קליפת העץ איננה חלקה והברק אינו מתקדם בקו ישר".
בחייו סבל מנדלברוט לא מעט בשל הפרקטלים. הממסד המתמטי ממש נידה אותו בשל ההתעסקות בתמונות, שלא יאה למתמטיקאי רציני. מי שהצילה אותו מחוסר תעסוקה הייתה חברת IBM, שלא זו בלבד שהעסיקה אותו במרכז המחקר שלה, אלא אף נתנה לו לעשות כרצונו. בעזרת חוק רקורסיבי פשוט מאוד הוא מצליח עתה לייצר תמונות בעלות מורכבות הולכת וגדלה, בה רואים ברמות שונות, כאמור, צורות דומות.
גם הציבור הרחב מתחיל להתחבר לרעיונות שלו, שבניגוד לרעיונות מתמטיים רגילים, קל להבינם. מה עוד שניתן היה לראותם לפתע, בתוצרי מחשב מודפסים. את הצד הגרפי של הפרקטלים ניתן היה גם לחקור וליישם באדריכלות, בעיצוב מוצר ובתעשיות שונות.
וכך זוכה מי שכילד בן 12 הפך לפליט פולני בצרפת ולימד את עצמו מתמטיקה לבדו, הוא זוכה בשלב מסוים בציבור לכינוי "כוכב הרוק של המתמטיקה". כי גם אם רעיונותיו על הפרקטלים עדיין לא מתקבלים אצל הקהילה המדעית, מעל ראשם הוא הופך די מהר לאחד המתמטיקאים המשפיעים בהיסטוריה.
קישורים מצורפים: